Integer Answer Type Questions: Vector Algebra and Three Dimensional Geometry | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q. 1. If 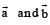 are vectors in space given by
are vectors in space given by 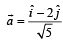 and
and 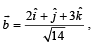 then find the value of
then find the value of 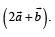
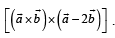 (2010)
(2010)
Ans. 5
Solution.
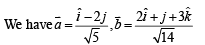
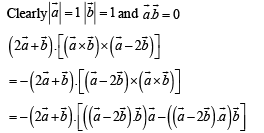
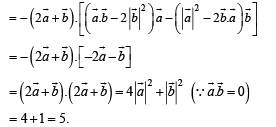
Q. 2. If the distance between the plane Ax – 2y + z = d and the plane containing the lines 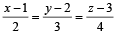 and
and 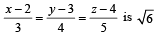 , then find |d|. (2010)
, then find |d|. (2010)
Ans. 6
Solution. The equation of plane containing the lines
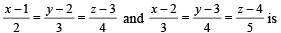
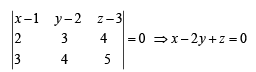
∴ Distance between x – 2 y +z=0 and Ax –2 y + z = d
= Perpendicular distance between parallel planes (∴ A= 1)
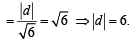
Q. 3. Let 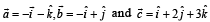 be three given vectors.
be three given vectors. 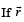 is a vector such that
is a vector such that 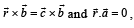 then the value of
then the value of 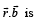 (2011)
(2011)
Ans. 9
Solution.
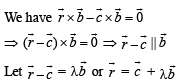
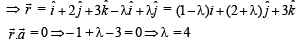
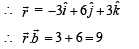
Q. 4. If 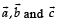 are unit vectors satisfying
are unit vectors satisfying 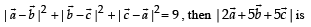 (2012)
(2012)
Ans. 3
Solution. 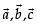 are units vectors such that
are units vectors such that
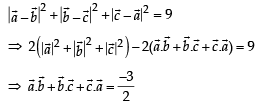
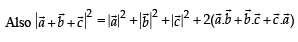
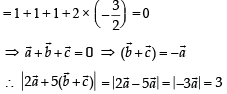
Q. 5. Consider the set of eight vectors 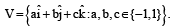 Three non- coplanar vectors can be chosen from V in 2p ways. Then p is (JEE Adv. 2013)
Three non- coplanar vectors can be chosen from V in 2p ways. Then p is (JEE Adv. 2013)
Ans. 5
Solution. Given 8 vectors are
(1, 1, 1), (–1, –1, –1); (–1, 1, 1), (1, –1, –1); (1, –1, 1),
(–1, 1, –1); (1, 1, –1), (–1, –1, 1)
These are 4 diagonals of a cube and their opposites.
For 3 non coplanar vectors first we select 3 groups of diagonals and its opposite in 4C3 ways. Then one vector from each group can be selected in 2 × 2 × 2 ways.
∴ Total ways = 4C3 × 2 × 2× 2 = 32 = 25
∴ p = 5
Q. 6. A pack contains n cards numbered from 1 to n . Two consecutive numbered cards are removed from the pack and the sum of the numbers on the remaining cards is 1224. If the smaller of the numbers on the removed cards is k, then k – 20 = (JEE Adv. 2013)
Ans. 5
Solution. Let k, k + 1 be removed from pack.
∴ (1 + 2 + 3 + ... + n) – (k + k + 1) = 1224
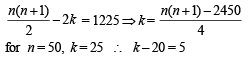
Q. 7. Let 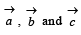 be three non-coplanar unit vectors suchthat the angle between every pair of them is π/3. If
be three non-coplanar unit vectors suchthat the angle between every pair of them is π/3. If 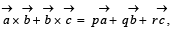 where p, q and r are scalars, then the value of
where p, q and r are scalars, then the value of 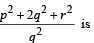 (JEE Adv. 2014)
(JEE Adv. 2014)
Ans. 4
Solution.
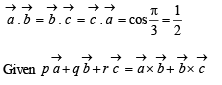
Taking its dot product with 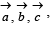 we get
we get
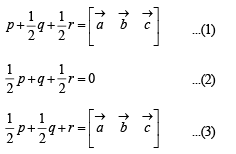
From (1) and (3), p = r Using (2) q = – p
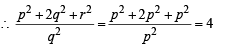
Q. 8. Suppose that 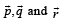 are three non-coplanar vectors in
are three non-coplanar vectors in 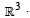 Let the components of a vector
Let the components of a vector 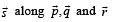 be 4, 3 and 5, respectively. If the components of this vector
be 4, 3 and 5, respectively. If the components of this vector 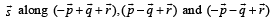 are x, y and z, respectively, then the value of 2x + y + z is (JEE Adv. 2015)
are x, y and z, respectively, then the value of 2x + y + z is (JEE Adv. 2015)
Ans. 9
Solution. 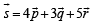
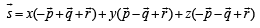
⇒ – x + y – z = 4
x – y – z = 3
x + y + z = 5
Solving above equation 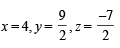
∴ 2x + y + z = 9
|
347 docs|185 tests
|
FAQs on Integer Answer Type Questions: Vector Algebra and Three Dimensional Geometry - JEE Advanced - 35 Years Chapter wise Previous Year Solved Papers for JEE
| 1. What is vector algebra and how is it related to three-dimensional geometry? |  |
| 2. How do you calculate the magnitude of a vector in three-dimensional space? |  |
| 3. What is the dot product of two vectors in three-dimensional space? |  |
| 4. How can vector algebra be applied to solve problems related to three-dimensional geometry? |  |
| 5. What is the cross product of two vectors in three-dimensional space and how is it useful in geometry? |  |




















