Pythagoras Theorem - Class 10 PDF Download
Pythagoras Theorem

The “Pythagorean theorem,” was inspired by the ancient Greek Mathematician Pythagoras who invented the theorem during 500 B.C. It has been argued that the “Ancient Babylonians” already understood the theorem long before the invention by Pythagoras. They knew the relationship between the sides of the triangle and while solving for the hypotenuse of an isosceles triangle, they came up with the approximate value of up to 5 decimal places.
What is Pythagoras theorem?
In a right-angled triangle, “The sum of squares of the lengths of the two sides is equal to the square of the length of the hypotenuse (or the longest side).”
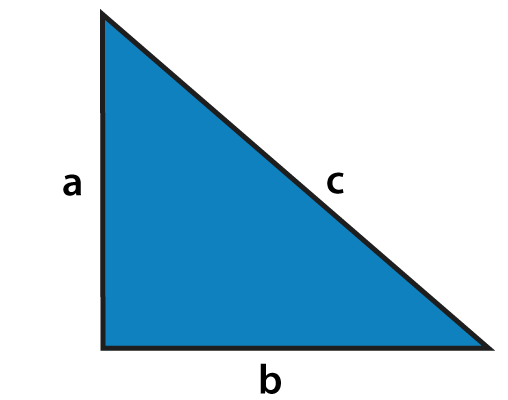
a2+b2=c2a2+b2=c2
In the given triangle, side “a” is called as “Perpendicular”, side “b” is called as “Base” and side “c” is called as “Hypotenuse.”
The side opposite to the right angle (90∘90∘) is the longest side known as Hypotenuse, as we know that the side opposite to the greatest angle is longest.
Another way of representation of the Pythagoras Theorem-
Another way of Pythagoras Theorem proof is described here. Consider a right-angled triangle having perpendicular as a, base as b, and hypotenuse as c. Consider three squares of sides a,b,c mounted on the three sides of a triangle having the same sides as shown.
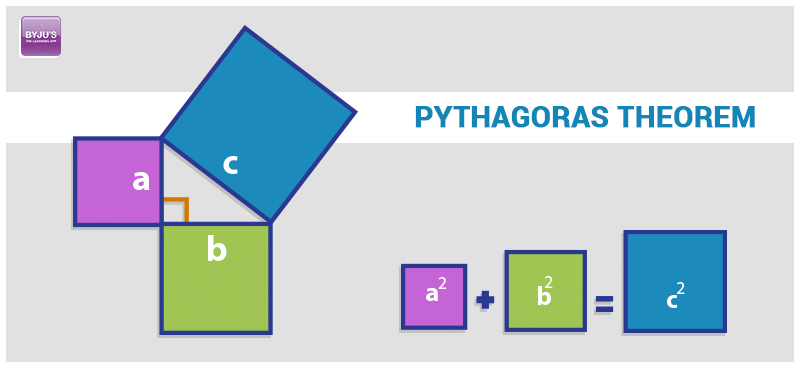
Area of square A + Area of square B = Area of square C
From Pythagoras Theorem we have,
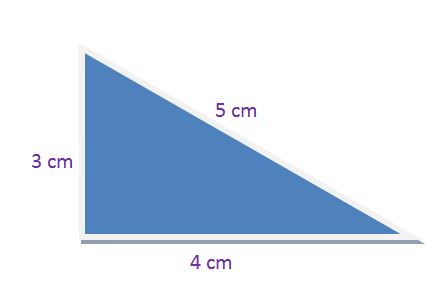
(Perpendicular)2+(base)2=(Hypotenuse)2(Perpendicular)2+(base)2=(Hypotenuse)2
Perpendicular = 3 cm
Base = 4 cm
Hypotenuse = 5 cm
(3)2+(4)2=(5)2(3)2+(4)2=(5)2
⇒9+16=25⇒9+16=25
⇒25=25⇒25=25
L.H.S. = R.H.S.
Therefore Pythagoras theorem is proved.
Proof of Pythagoras Theorem-
To Prove- AC2=AB2+BC2AC2=AB2+BC2</p >
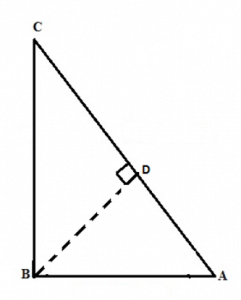
For this we drop a perpendicular BD onto the side AC
We know, △ADB∼△ABC△ADB∼△ABC
Therefore, ADAB=ABACADAB=ABAC (Condition for similarity)
Or, AB2=AD×ACAB2=AD×AC……..(1)
Also, △BDC∼△ABC△BDC∼△ABC
Therefore, CDBC=BCACCDBC=BCAC (Condition for similarity)
Or, BC2=CD×ACBC2=CD×AC……..(2)
Adding the equations (1) and (2) we get,
AB2+BC2=AD×AC+CD×ACAB2+BC2=AD×AC+CD×AC
AB2+BC2=AC(AD+CD)AB2+BC2=AC(AD+CD)
Since, AD + CD = AC
Therefore, AC2=AB2+BC2AC2=AB2+BC2
Application-
(1st): To know the triangle is right-angled or not. It is to be noted that if the Pythagoras Theorem is proved then it must be a right-angled triangle.
To prove- Pythagoras theorem in order to find whether it has a right angle or not
From Pythagoras Theorem, we have-
(Perpendicular)2+(base)2=(Hypotenuse)2(Perpendicular)2+(base)2=(Hypotenuse)2
Perpendicular = 12 units
Base = 5 units
Hypotenuse = 13 units
(12)2+(5)2=(13)2(12)2+(5)2=(13)2
⇒144+25=169⇒144+25=169
⇒169=169⇒169=169
L.H.S. = R.H.S.
Therefore the angles opposite to the 13 unit side will be at a right angle.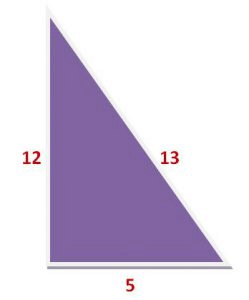
FAQs on Pythagoras Theorem - Class 10
| 1. What is Pythagoras Theorem? |  |
| 2. How is Pythagoras Theorem used in real life? |  |
| 3. How can Pythagoras Theorem be proved? |  |
| 4. Can Pythagoras Theorem be applied to non-right-angled triangles? |  |
| 5. What are some practical examples of Pythagoras Theorem? |  |













