JEE Advanced (Subjective Type Questions): States of Matter- 2 | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.17. An LPG (liquefied petroleum gas) cylinder weighs 14.8 kg when empty. When full, it weighs 29.0 kg and shows a pressure of 2.5 atm. In the course of use at 27º C, the weight of the full cylinder reduces to 23.2 kg. Find out the volume of the gas in cubic meters used up at the normal usage conditions, find the final pressure inside the cylinder.
 Assume LPG to be n-butane with normal boiling point of 0ºC. (1994 - 3 Marks) 

Ans. Sol. Calculation of volume of gas : Weight of cylinder with gas = 29.0 kg
Weight of empty cylinder = 14.8 kg
∴ Weight of gas in the cylinder = 14.2 kg Pressure in cylinder = 2.5 atm
∴ No. of moles (n) in 14.2 kg (14.2 × 10³g) of butane

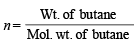
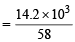= 244.83 mol

Applying gas equation,

= 2412 litres
[27°C = 273 + 27 = 300]
Calculation of pressure in cylinder after use.
Weight of cylinder after use = 23.2 kg
Weight of empty cylinder = 14.8 kg
∴ Wt. of unused gas = 8.4 kg 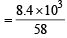 moles of butane

Thus P = 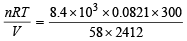= 1.478 atm [V = 2412 L]

Calculation of volume of used gas at 2.5 atm and 27ºC.
Weight of used gas = 14.2 – 8.4 = 5.8 kg
Pressure under normal usage conditions = 1 atm

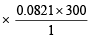
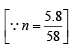
= 2463 litres = 2.463 m³

Q.18. A mixture of ethane (C₂H₆) and ethene (C₂H₄) occupies 40 litres at 1.00 atm and at 400 K. The mixture reacts completely with 130 g of O₂ to produce CO₂ and H₂O. Assuming ideal gas behaviour, calculate the mole fractions of C₂H₄ and C₂H₆ in the mixture. (1995 - 4 Marks) 

Ans. Sol. Let the volume of ethane in mixture = x litre

∴ Volume of ethene = (40 – x) litre

Combustion reactions of ethane and ethene are :

(i)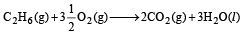 

or 2C₂ H₆ (g) + 7O₂ (g) ¾¾→ 4CO₂ (g) + 6H₂O(l )

(ii) C₂H₄(g) + 3O₂(g) ¾¾→ 2CO₂(g) + 2H₂O(l )

Volume of O₂ required for complete combustion of ethane

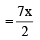[For x litres]

Volume of O₂ required for complete combustion of ethene = (40–x) × 3 [For (40 – x) L]

∴ Total volume of  O₂ required

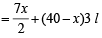
Calculation of number of moles (n)

P = 1 atm, 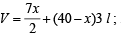   R = 0.082 l atm K^–1 mol^–1;

T = 400 K

Since  n =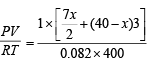 

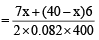
Mass of n moles of O₂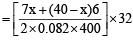 = 130

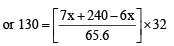
⇒ 8528 = 32 x + 240 × 32 ⇒ 32x = 848 ⇒ or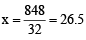

Hence mole fraction (%) of ethane  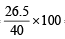= = 66.25%

Mole fraction (%) of ethene = 33.75%

Q.19. The composition of the equilibrium mixture ( Cl2 2Cl ), which is attained at 1200°C, is determined by measuring the rate of effusion through a pin–hole. It is observed that at 1.80 mmHg pressure, the mixture effuses 1.16 times as fast as krypton effuses under the same conditions. Calculate the fraction of the chlorine molecules dissociated into atoms. (Relative atomic mass of Kr = 84.) (1995 - 4 Marks)

Ans. Sol. Mixture           Kr ypton
r_mix  = 1.16           r_Kr = 1
M_mix = ?               M_Kr = 84

We know that

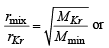
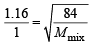
or (1.16)²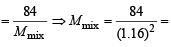62.426

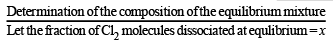
Initially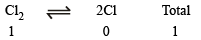             

At equilibrium    1 – x                2x          1– x + 2x = 1 + x

∴ Total moles at equilibrium  = 1 – x + 2x = 1 + x

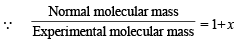
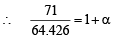
∴ a = 0.137 = 13.7%.

Q. 20. A 20.0 cm³ mixture of CO, CH₄ and He gases is exploded by an electric discharge at room temperature with excess of oxygen. The volume contraction is found to be 13.0 cm³. A further contraction of 14.0 cm³ occurs when the residual gas is treated with KOH solution. Find out the composition of the gaseous mixture in terms of volume percentage. (1995 - 4 Marks)

Ans. Sol. TIPS/Formulae :
(i) He does not react with oxygen.
(ii) KOH absorbs only CO₂.
NOTE : When the mixture of CO, CH₄ and He gases (20 ml) are exploded by an electric discharge with excess of O₂, He gas remains as such and the other reactions involved are :

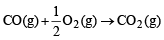             ...(i)

CH₄ (g ) + 2O₂ (g) → CO₂ (g) + 2H ₂O(l) ...(ii)

Let the volumes of CO and CH₄ to be ‘a’ ml and ‘b’ ml in the mixture then
Volume of He gas = [20 – (a + b)] ml
For the initial contraction of 13 ml,
Volume of left hand side in the above reactions – 13 = Volume of right hand side

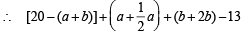
    = [20 – (a + 2b)] + a + b      [neglect the volume of H₂O (l)](Since for gases, volume a no. of moles)

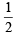∴  a + 2 b = 13  or     a + 4 b = 26 ...(iv)

NOTE THIS STEP : The CO₂ produced above in reactions (ii) & (iii), (a + b) ml, reacts with KOH sol for a further contraction of 14 ml.
CO₂(g) + 2KOH(l) → K₂ CO₃(l) + H₂O(l) (a + b) ml
∴ a + b = 14 ...(v)
Solving (iv) & (v) we get, a = 10 ml & b = 4 ml

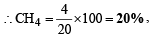
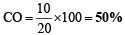
&  He = 100 – ( 20 + 50) = 30%

Q. 21. An evacuated glass vessel weighs 50.0 g when empty, 148.0 g when filled with a liquid of density 0.98 g mL^–1 and 50.5 g when filled with an ideal gas at 760 mmHg at 300K. Determine the molar mass of the gas. (1998 -  3 Marks) 

Ans. Sol. Weight of liquid = 148 – 50 = 98 g

Volume of liquid = 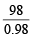= 100 ml = volume of vessel It means, vessel of 100 ml contains ideal gas at 760 mm  Hg at 300 K

Weight of gas = 50.5 – 50 = 0.5g

using,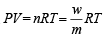 

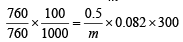
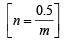
∴   Molecular weight of gas (m) = 123

Q.22. The degree of dissociation is 0.4 at 400 K and 1.0 atm for the gaseous reaction PCl₅ PCl₃ + Cl₂. Assuming ideal behaviour of all gases, calculate the density of equilibrium mixture at 400 K and 1.0 atmosphere. (Relative atomic mass of  P = 31.0 and Cl = 35.5) (1998 -  3 Marks) 

Ans. Sol.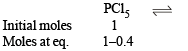 

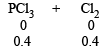
∴ Total moles at equilibrium = 1 – 0.4 + 0.4 + 0.4  = 1.4  

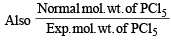= 1 + a = 1.4

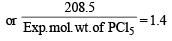
∴ Exp. mol. wt. of PCl₅ or m. wt. of mixture =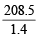

Now using, 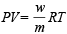 for mixture

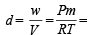
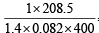= 4.53 g/litre

Q.23. Using van der waal’s equation, calculate the constant, ‘a’ when two moles of a gas confined in a four litre flask exerts a pressure of 11.0 atmospheres at a temperature of 300 K.
 The value of ‘b’ is 0.05 L mol^–1. (1998 -  4 Marks) 

Ans. Sol. van der Waals equation for n moles of gas is

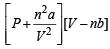 = nRT

Given   V = 4 litre; P = 11.0 atm, T = 300 K; b = 0.05 litre mole^–1, n =2

Thus, 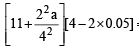 = 2 x 0.082 x 300

∴ a = 6.46 atm litre² mol^–2

Q.24. For the reaction, N₂O₅(g) → 2NO₂(g) + 0.5 O₂(g), calculate the mole fraction of N₂O₅(g) decomposed at a constant volume and temperature, if the initial pressure is 600 mm Hg and the pressure at any time is 960 mm Hg. Assume ideal gas behaviour. (1998 -  3 Marks) 

Ans. Sol.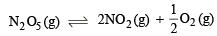                        

Initial pressure              600       0                       0
Final pressure              600-P      2P                    P/2
P ∝ moles when V and T are constant (where moles equivalent to pressure P are decomposed)
Total pressure = 600 – P + 2 P + P/2 = 960 mm of Hg
∴ P = 240 mm Hg
Thus moles of N₂O₅ decomposed =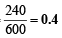

Q.25. One mole of nitrogen gas at 0.8 atm takes 38 s to diffuse through a pinhole, whereas one mole of an unknown compound of xenon with flourine at 1.6 atm takes 57 s to diffuse through the same hole. Calculate the molecular formula of the compound. (1999 - 5 Marks) 

Ans. Sol. We know that

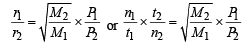
∴ M = 252

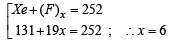
Thus compound of xenon with fluorine is XeF₆

Q.26. The pressure exerted by 12 g of an ideal gas at temperature t°C in a vessel of volume V litre is one atm. When the temperature is increased by 10 degrees at the same volume, the pressure increases by 10%. Calculate the temperature t and volume V. (Molecular weight of the gas = 120.) (1999 - 5 Marks)

Ans. Sol. (I) Given P = 1 atm, w = 12 g; T = (t + 273)K; V = V litre
(II) If T = t + 10 + 273 = t + 283 K ; V =  V litre,

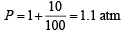
Using gas equation,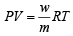  

Case I.  1 x V 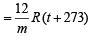   ... (1)

Case I. 1.1 x V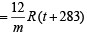    ...(2)

From (1) and (2),  t = –173ºC    or  t = 100 K

Also from (1), on substituting t and m (120),  V = 0.82 litre

Q.27. Calculate the pressure exerted by one mole of CO₂ gas at 273 K if the van der Waal's constant a = 3.592 dm⁶ atm mol^–2. Assume that the volume occupied by CO₂ molecules is negligible. (2000 - 2 Marks)

Ans. Sol. 

vander Waals’ equation for one mole of a gas is

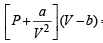= RT          ...(1)

Given that volume occupied by CO₂ molecules, ‘b’ = 0

Hence, (1) becomes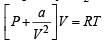

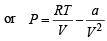
Using R = 0.082, T = 273K, V = 22.4 l for 1 mole of an ideal gas at 1 atm pressure.

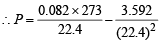= 0.9922 atm.

Q. 28. The compression factor (compressibility factor) for one mole of a van der Waals gas at 0°C and 100 atmospheric pressure is found to be 0.5. Assuming that the volume of a gas molecule is negligible, calculate the van der Waals constant a. (2001 - 5 Marks) 

Ans. Sol. We know that, Compressibility factor ,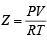 

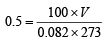               ∴  V = 0.1119L

NOTE : Further when volume of a gas molecule is negligible, van der Waal’s equation becomes

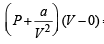 = RT

or PV = RT - 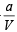 or  a = RTV- PV²

Substituting the values a = (0.082 × 0.1119 × 273) – (100 × 0.1119 × 0.1119)

  = 1.253 atm L² mol^–2

Q.29. The density of the vapour of a substance at 1 atm pressure and 500 K is 0.36 kgm^-3. The vapour effuses through a small hole at a rate of 1.33 times faster than oxygen under the same condition. (2002 - 5 Marks)
 (a) Determine (i) molecular weight, (ii) molar volume, (iii) compression factor (Z) of the vapour and (iv) which forces among the gas molecules are dominating, the attractive or the repulsive?
 (b) If the vapour behaves ideally at 1000 K, determine the average translational kinetic energy of a molecule. 

Ans. Sol. (a) d = 0.36 kg m^–3  = 0.36 g/L (i)

From Graham’s Law of diffusion

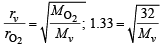
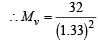= 18.09;

where  M_v = MW of the vapour

(ii) Thus, 0.36g =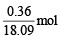 

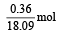occupies 1 L volume,  so 1 mol occupies

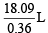= 50.25L

Thus, molar volume of vapour = 50.25 L

Assuming ideal behaviour the volume of the vapour can be calculated by

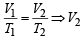
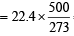 = 41.025L

(iii) Compressibility factor (Z)

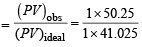 = 1.224

(iv) Z is greater than unit y, hence it is the shor t range repulsive force that would dominate. (∵ actual density is less than given density)

(b)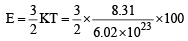

= 2.07 x 10^-20 J per molecule                    
(∵ K, Boltzmann constant = R/N)

Q.30. The average velocity of gas molecules is 400 m/sec. Calculate its rms velocity at the same temperature. (2003 - 2 Marks)

Ans. Sol. TIPS/Formulae :

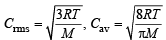
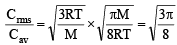 = 1.085

C rms = 1.085 × C_av  = 1.085 × 400 = 434 ms^–1

Q. 31. A graph is plotted between PVm along Y-axis and  P along X-axis, where Vm is the molar volume of a real gas. Find the intercept along Y-axis. (2004 - 2 Marks)

Ans. Sol. The van der Waal equation (for one mole) of a real gas is

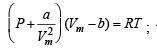
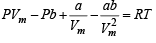
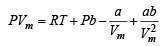 ...(i)

NOTE THIS STEP : To calculate the intercept P → 0, hence V_m → ∞ due to which the last two terms on the right side of the equation (i) can be neglected.
∴ PV_m = RT + Pb
When P = 0, intercept = RT