JEE Advanced (Fill in the Blanks): Rotational Motion | Chapter-wise Tests for JEE Main & Advanced PDF Download
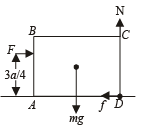
Q.1. A uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point that is directly above the centre of the face, at a height 3a/4 above the base. The minimum value of F for which the cube begins to tip about the edge is .... (Assume that the cube does not slide). (1984 - 2 Marks)
Ans. 2/3
Solution.
KEY CONCEPT
When the cube begins to tip about the edge the normal reaction will pass through the edge about which rotation takes place. The torque due to N and f will be zero.
Taking moment of force about D
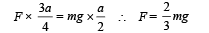
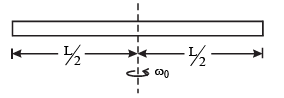
Q.2. A smooth uniform rod of length L and mass M has two identical beads of negligible size, each of mass m, which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity w0 about an axis perpenducular to the rod and passing through the midpoint of the rod (see figure). There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......... (1988 - 2 Marks)
Ans.
Solution. Note : Since no external force and hence no torque is applied, the angular momentum remains constant ∴ I1w1 = I2w2
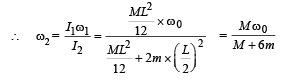
Q.3. A cylinder of mass M and radius R is resting on a horizontal platform (which is parallel to the x–y plane) with its axis fixed along the y-axis and free to rotate about its axis. The platform is given a motion in the x-direction given by x = A cos ( w t). There is no slipping between the cylinder and platform. The maximum torque acting on the cylinder during its motion is ..................
Ans.
Solution. Considering the motion of the platform
x = A cos ωt
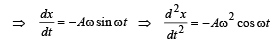
The magnitude of the maximum acceleration of the platform is
∴ | Max acceleration | = Aω2
When platform moves a torque acts on the cylinder and the cylinder rotates about its axis.
Acceleration of cylinder,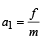
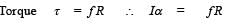
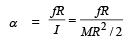
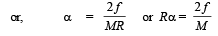
∴ Equivalent linear acceleration (Rα=a2)
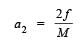
∴ Total linear acceleration,
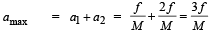
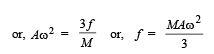
Thus, maximum torque,
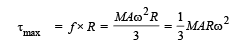
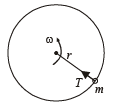
Q.4. A stone of mass m, tied to the end of a string, is whirled around in a horizontal circle. (Neglect the force due to gravity). The length of the string is reduced gradually keeping the angular momentum of the stone about the centre of the circle constant. Then, the tension in the string is given by T = Arn where A is a constant, r is the instantaneous radius of the circle and n = .....
Ans. -3
Solution. Let at any instant of time t, the radius of the horizontal surface be r.

Where m is the mass of stone and w is the angular velocity at that instant of time t.

From (i) and (ii)
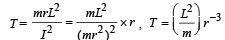
= Ar -3
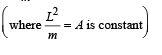
Thus, n = –3
Q.5. A rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A . The normal reaction on A is... and on B is.....
Ans.
Solution.
RA + RB = W
∴RA = W – RB
Q.6. A symmetric lamina of mass M consists of a square shape with a semicircular section over of the edge of the square as shown in Fig. P-10. The side of the square is 2a.
The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is 1.6 Ma2. The moment of inertia of the lamina about the tangent AB in the plane of the lamina is....

Ans. 4.8 Ma2
Solution. Assuming symmetric lamina to be in xy plane, we will have Ix = Iy (Since the mass distribution is same about x-axis and y-axis)
Ix + Iy = Iz (perpendicular-axis theorem)
It is given that Iz = 1.6 Ma2.
Hence
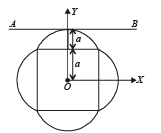
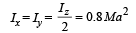
Now, according to parallel-axis theorem, we get
IAB = Ix + M(2a)2
= 0.8 Ma2 + 4Ma2
= 4.8 Ma2
|
446 docs|930 tests
|





















