Can anyone exaplain L Hospital Rule ?
Ref: https://edurev.in/question/732001/Can-anyone-exaplain-L-Hospital-Rule-
L’Hospital’s Rule is a method for finding the value of certain kinds of limits using derivatives. The rule is named after Guillaume de l’Hospital (or l’Hôpital), which is a French name, pronounced low-pee-tal(NOT le Hoss-pih-tal).

L’Hospital’s Rule
If f(x)/g(x) has the form 0/0 or ∞/∞ when x = a is plugged in, then:
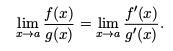
In other words, take the derivative of the numerator (top) and the derivative of the denominator (bottom), and then try computing the limit.
Using L’Hospital’s Rule
In order to use l’Hospital’s Rule, you must first check to see that your limit has the right form.
First of all, it must be a fraction of two functions, f(x) / g(x) in order to apply the rule.
Secondly — and this is crucial! — when you plug in the given x-value, the fraction must either evaluate to 0/0 or ∞/∞. These are two types of indeterminate forms. If your limit problem is not in an indeterminate form, then you can’t use this method directly.
Examples
Let’s see how l’Hospital’s Rule works in the following two examples.
Example 1

After plugging in x = 0, we find the indeterminate form, 0/0. So l’Hospital’s Rule can be used. Just take the derivative of the top and the derivative of the bottom. Afterwards, try plugging in the x value again.
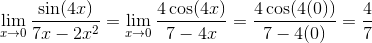
Example 2
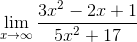
L’Hospital’s Rule works just as well in limits as x → ± ∞. Notice, the indeterminate form this time is ∞/∞.
But there’s another interesting feature about this example. After using the rule once, the limit still has indeterminate form (∞/∞). Therefore, we can use the rule once again.
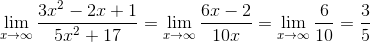
In general, l’Hospital’s Rule may be repeated as many times as necessary, as long as there is an indeterminate form at each stage.
Functions that are not Fractions
Sometimes a limit problem comes along that seems impossible to do. Standard algebraic techniquesmay not work. If the function had a fractional form, then we could use l’Hospital. But what if the function is not even a fraction?
There are certain algebraic manipulations that can force an expression to be a fraction. When done correctly, l’Hospital may be used on the result.
Forcing a Fraction
Here is an example in which we change a product into a fraction using a standard algebraic trick.
Example 3
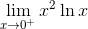
This time we didn’t start with a fraction. But if you rewrite x2 = 1/x -2 using negative exponents, then we can force the function to take the form of a fraction. Then use l’Hospital’s Rule on the result.
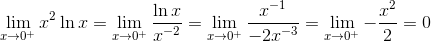
FAQs on L’Hospital’s Rule - JEE
| 1. What is L'Hospital's rule in JEE? |  |
| 2. How do I apply L'Hospital's rule in JEE? |  |
| 3. Can L'Hospital's rule be used for all limits in JEE? |  |
| 4. Are there any limitations or conditions to apply L'Hospital's rule in JEE? |  |
| 5. Can L'Hospital's rule be used to find limits at infinity in JEE? |  |


















