JEE Advanced (Matrix Match & Integer Answer): Electrostatics | Chapter-wise Tests for JEE Main & Advanced PDF Download
Match the Following
DIRECTIONS (Q. No. 1) : Each question contains statements given in two columns, which have to be matched. The statements in Column-I are labelled A, B, C and D, while the statements in Column-II are labelled p, q, r and s. Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in Column-II. The appropriate bubbles corresponding to the answers to these questions have to be darkened as illustrated in the following example :
If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of

Q.1. Six point charges, each of the same magnitude q, are arranged in different manners as shown in Column-II. In each case, a point M and line PQ passing through M are shown. Let E be the electric field and V be the electric potential at M (potential at infinity is zero) due to the given charge distribution when it is at rest. Now, the whole system is set into rotation with a constant angular velocity about the line PQ. Let B be the magnetic field at M and m be the magnetic moment of the system in this condition.
Assume each rotating charge to the equivalent to a steady current. (2009)
| Column-I | Column-II | |
| (A) E = 0 | 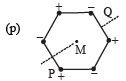 | Charges are at the corners of a regular hexagon. M is at the centre of the hexagon. PQ is perpendicular to the plane of the hexagon |
| (B) V ≠ 0 | 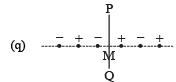 | Charges are on a line perpendicular to PQ at equal intervals. M is the mid-point between the two innermost charges. |
| (C) B = 0 | 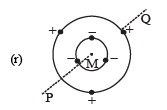 | Charges are placed on two coplanar insulating rings at equal intervals. M is the common centre of the rings. PQ is perpendicular to the plane of the rings. |
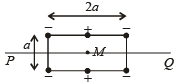
| (D) μ ≠ 0 | 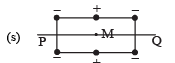 | Charges are placed at the corners of a rectangle of sides a and 2a and at the mid points of the longer sides. M is at the centre of the rectangle. PQ is parallel to the longer sides. |
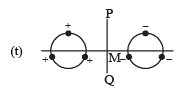 | Charges are placed on two coplanar, identical insulating rings at equal intervals. M is the mid-point between the centres of the rings. PQ is perpendicular to the line joining the centres and coplanar to the rings. |
Ans. (A)-(p, r, s): (B)-(r, s); (C)-(p, q, t); (D)-(r, s)
Solution.
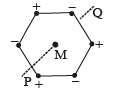
The electric field at M due to the charges at the corners of regular hexagon is as shown

Here | E+ | = |E- |. The symmetry of the situation shows that E = 0 at M.
Therefore (A) is the correct option.
The electric potential due to all the charges at M is zero.
Therefore (B) is incorrect option.
When the system of charges is rotated about line PM, the net current will be zero.
Therefore the magnetic field at M is zero.
(C) is the correct option.
When magnetic field is zero, then μ = 0
(D) is incorrect option.
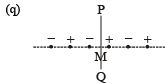
The electric field due to the inner most positive and negative charges at M is 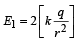 towards left. The electic fielddue to the next positive and negative charges at M is
towards left. The electic fielddue to the next positive and negative charges at M is
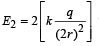 towards right. The electric field due tothe outermost positive and negative charges at M is
towards right. The electric field due tothe outermost positive and negative charges at M is 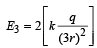
towards left. Clearly the vector sum ofthese three electric field is not zero.
(A) is incorrect option.
The electric potential due to the charges at M
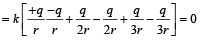
(B) is incorrect option.
The net current due to the innermost positive and negative charges is zero. Similarly the net current due to other charges in pairs is zero. Therefore the magnetic field at M is zero.
Also the magnetic moment is zero.
(C) is the correct option
(D) is incorrect option.
(r)
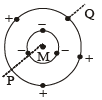
The net electric field due to negative charges in the inner circle is zero.
Similarly the net electric field due to positive charges in the outercircle is zero.
(A) is the correct option.
The electric potential due to negative charges at M is different from the electric potential due to positive charges at M. Therefore the electric potential at M is not equal to zero.
(B) is the correct option.
When the system of charges rotate, we get a current I1 due to negative charges and another current I due to positive charges. The magnitude of the magnetic at M due to the currents is different. Therefore B ≠ 0 and μ ≠ 0.
(C) is incorrect option
(D) is the correct option.
(s)
The electric field at M due to all the charges is zero because the electric field due to different charges cancel out in pairs.
(A) is the correct option.
The potential at M due to the charges is
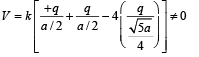
(B) is the correct option.
When the whole system is set into rotation with a constant angular velocity about the line PQ we get three loops in which current is flowing.
The magnetic field due to these currents produce a resultant magneic field at M which is not equal to zero. Therefore a net magnetic dipole moment will be produced.
(C) is an incorrect option.
(D) is correct option.
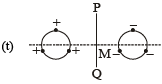
There will be a net electric field due to the arrangement of charges at M towards the right side.
(A) is an incorrect option.
The electic potential at M will can out in pairs by positive and negative charges, due to symmetrical arrangement of charges.
(B) is an incorrect option.
When the system of charges rotates about PQ, the net current is zero due to symmetrical arrangement of charges.
Therefore B = 0 and μ = 0
(C) is the correct option.
(D) is the incorrect option.
DIRECTIONS (Q. No. 2) : Following question has matching lists. The codes for the lists have choices (a), (b), (c) and (d) out of which ONLY ONE is correct.
Q.2. Four charges Q1, Q2, Q3 and Q4 of same magnitude are fixed along the x axis at x = – 2a, – a, + a and + 2a, respectively. A positive charge q is placed on the positive y axis at a distance b > 0. Four options of the signs of these charges are given in List-I. The direction of the forces on the charge q is given in List-II. Match List-I with List-II and select the correct answer using the code given below the lists.
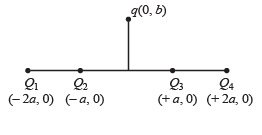
| List - I | List - II |
| P. Q1, Q2, Q3, Q4 all positive | 1. + x |
| Q. Q1, Q2 positive Q3, Q4 negative | 2. – x2. – x |
| R. Q1, Q4 positive; Q2, Q3 negative | 3. + y |
| S. Q1, Q3 positive; Q2, Q4 negativ | 4. – y |
Codes:
(a) P-3, Q-1, R-4, S-2
(b) P-4, Q-2, R-3, S-1
(c) P-3, Q-1, R-2, S-4
(d) P-4, Q-2, R-1, S-3
Ans. (a)
Solution. If Q1, Q2, Q3 and Q4 are all positive, then the force will be along + y-direction.
If Q1, Q2 are positive and Q3, Q4 are negative the force will act along + x-direction.
If Q1, Q4 are positive and Q2, Q3 are negative then attractive force will dominate repulsive force and the force will be along – y direction.
Integer Value Correct Type
Q.1. A solid sphere of radius R has a charge Q distributed in its volume with a charge density ρ = kra, where k and a are constants and r is the distance from its centre.
If the electric field at 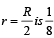 times that at r = R, find the value of a. (2009)
times that at r = R, find the value of a. (2009)
Ans. 2
Solution. Let us consider a spherical shell of radius x and thickness dx. The volume of this shell is 4px2(dx). The charge enclosed in this spherical shell is

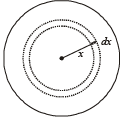
For r = R :
The total charge enclosed in the sphere of radius R is

∴ The electric field at r = R is
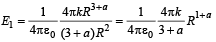
For r = R/2 :
The total charge enclosed in the sphere of radius R/2 is
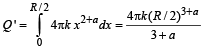
∴ The electric field at r = R/2 is
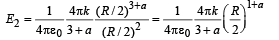
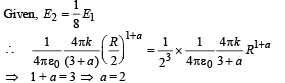
Q.2. Four point charges, each of +q, are rigidly fixed at the four corners of a square planar soap film of side ‘a’. The surface tension of the soap film is γ. The system of charges and planar film are in equilibrium, and 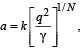
where ‘k’ is a constant. Then N is (2011)
Ans. 3
Solution. 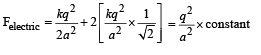
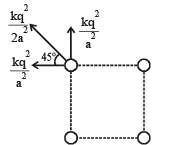
As the system of charges and planar film is in equlibrium, therefore

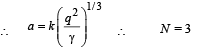
Q.3. An infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of the cylinder, as shown in the figure. The magnitude of the electric field at the point P, which is at a distance 2R from the axis of the cylinder, is given by the expression 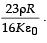 The value of k is (2012)
The value of k is (2012)
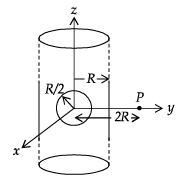
Ans. 6
Solution. We suppose that the cavity is filled up by a positive as well as negative volume charge of r. So the electric field now produced at P is the superposition of two electric fields. (a) The electric field created due to the infinitely long solid cylinder is
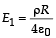 directed towards the +Y direction
directed towards the +Y direction
(b) The electric field created due to the spherical negative charge density
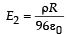 directed towards the –Y direction.
directed towards the –Y direction.
∴ The net electric field is
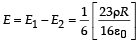
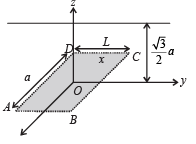
Q.4. An infinitely long uniform line charge distribution of charge per unit length λ lies parallel to the y-axis in the y – z plane at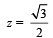 a (see figure). If the magnitude of the flux of theelectric field through the rectangular surface ABCD lying in the x – y plane with its centre at the origin is
a (see figure). If the magnitude of the flux of theelectric field through the rectangular surface ABCD lying in the x – y plane with its centre at the origin is 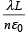
(ε0 = permittivity of free space), then the value of n is (JEE Adv. 2015)
Ans. 6
Solution.
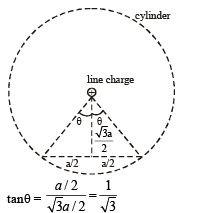
∴ θ = 30°
The flux through the dotted cylinder by Gauss’s law is
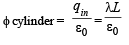
∴ For 360° angle the flux is 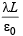
∴ For 60° angle the flux will be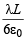
Therefore n = 6
|
446 docs|929 tests
|
















