Surface Area and Volume Exercise 16.1(Part-2) - Class 10 PDF Download
Question 22: A well of diameter 3m is dug up to 14m deep. The earth taken out of it has been spread evenly all around it to a width of 3m to form an embankment. Find the height of the embankment.
Sol:
Given
Diameter of the well = 3 m
Radius of the well = 3/2 m = 1.5m
Depth of the well = 14 m
Width of the embankment = 4 m
Radius of the outer surface of the embankment = 4+ 3/2 m = 5.5 m
Let the height of the embankment be = h m
Volume of the embankment 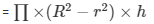
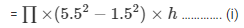
Volume of earth dug out = 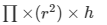
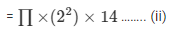
Comparing both the equations we get,
H = 9/8 m
Height of the embankment is 9/8 m
Question 23: Find the volume largest right circular cone that can be cut out of a cone of a cube whose edge is 9 cm.
Solution:
Given,
The side of the cube = 9 cm
The largest cone is curved from cube diameter of base of cone = side of the cube
2r = 9
r = 9/2 cm = 4.5 cm
Height of cone = side of cube
Height of cone (h) = 9 cm
Volume of the largest cone to fit in 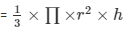
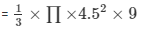
=190.92 cm³
The volume of the largest cone to fit in is having a volume of 190.92 cm³
Question 24: Rain water which falls on a flat rectangular surface of length 6m and breadth 4m is transferred into a cylindrical vessel of internal radius 20 cm .What will be the height of water in the cylindrical vessel if a rainfall of 1cm has fallen?
Solution:
Given,
Length of the rectangular surface = 6 m = 600 cm
Breadth of the rectangular surface =4m = 400cm
Height of the perceived rain = 1 cm
Volume of the rectangular surface = length * breadth * height
=600*400*1 cm³
=240000 cm³ …………………………… (i)
Given,
Radius of the cylindrical vessel =20 cm
Let the height of the cylindrical vessel = h cm
Volume of the cylindrical vessel 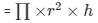
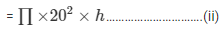
Since rains are transferred to cylindrical vessel
So, equating both the above marked equations:
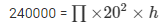
H =190.9 cm
The height of the cylindrical vessel is 190.9 cm.
Question 25: A conical flask of water. The flask has base radius(r) and height (h). The water is poured into a cylindrical flask of base radius Mr. Find the height of water in the cylindrical flask?
Solution
Given:
Base radius of the conical flask = r m
Height of the conical flask = h m
Volume of the cone 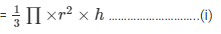
Given,
Base radius of the cylindrical flask is Mr.
Let the height of the flask be h1.
Volume of the cylinder 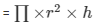
It’s volume 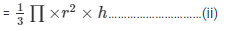
Since water in conical flask is poured into cylindrical flask their volumes are same.
So, equations i and ii are same .
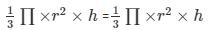
h1= h/3m2
The required height of the cylindrical vessel is h/3m2.
Question 26: A rectangular tank is 15 m long and 11m in breadth is required to receive entire liquid contents from a full cylindrical tank of internal diameter 21 m and length 5 m .Find the least height of the tank that will serve the purpose?
Solution:
Given,
Length of the rectangular tank = 15 m
Breadth of the rectangular tank = 11 m
Let the height of the rectangular tank be =h m
Volume of the rectangular tank = length *breadth * height
=15*11*h m3 …………………………………………. (i)
Given,
Radius of the cylindrical tank = 21/2 m = 10.5 m
Height of the tank = 5 m
Volume of the cylindrical tank 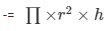
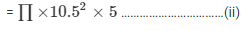
Since equation i and ii are having same volumes so, equating both equations
We get,
165 * h 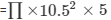
h= 10.5 m
The height of the tank is 10.5 m.
Question 27: A hemispherical bowl of internal radius 9 cm is full of liquid. This liquid is to be filled into cylindrical shaped small bottles each of diameter 3 cm and height 4 cm. How many bottles are necessary to empty the bowl?
Solution:
Given,
The internal radius of the hemispherical bowl = 9 cm
Volume of the hemisphere 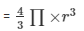
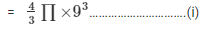
Given,
Diameter of the cylindrical bottle = 3 cm
Radius = 3/2 cm = 1.5 cm
Volume of the cylinder 
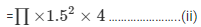
Volume of the hemispherical bowl is equals to (n) multiplied by volume of the cylindrical bottles.
Now,
Comparing equations i and ii,
We get,
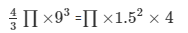
N= 54
54 cylindrical bottles are required to empty a hemispherical bowl.
Question 28: A cylindrical tube of radius 12 cm contains water to a depth of 20 cm. A spherical ball is dropped into the tube and the level of water is raised by 6.75 cm. Find the radius of the ball?
Solution:
Given,
The radius of a cylindrical tube (r) =12 cm
Level of water raised in the tube (h) = 6.75 cm
Volume of the cylinder 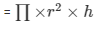
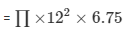
Let r be the radius of the spherical ball
Volume of the sphere
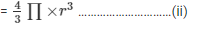
To find the radius of the spherical ball of unknown radius r we need to equate equations i and ii
We get,
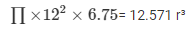
r³ = 729
r = 9 cm
The radius of the spherical ball is 9 cm.
Question 29: 500 persons have to dip in a rectangular tank which is 80 m long and 50 m broad. What is the rise in the level of water in the tank, if the average displacement of water by a person is 0.04m³?
Solution:
Given,
The length of a rectangular tank (l) = 50 m
Breadth of the rectangular tank (b) = 10 m
Total displacement of water in a rectangular tank by 400 persons = 400* 0.02 m³
=8 m³ ……………………….(i)
Let the depth of tank be h m
Volume of the rectangular tank = length * breadth * height
= l* b* h
=50*10* h m³ = 500hm³ ………………………………….(ii)
Now equating equations i and ii, we get ,
8 = 500* h
H = 0.016 m
The rise in water level of the rectangular tank is 0.016m.
Question 30: A cylindrical jar of radius 6cm contains oil. Iron spheres each of radius 1.5 cm are immersed in the oil. How many spheres are necessary to raise the level of the oil by 2 cm?
Solution:
Given,
The radius of the cylindrical jar (r) = 6 cm
Height of the cylindrical jar (h) = 2 cm
Let the number of balls be (n)
Volume of the cylinder = 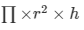
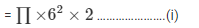
Let the Radius of the sphere be 1.5 cm
Volume of the sphere 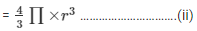
Volume of the cylindrical jar is equal to the sum of volume of (n) number of spheres.
Now, equating equations I and ii we get,
\(\prod \times 6^{2}\times 2[/latex 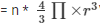 \(\frac{4}{3}\prod \times r^{3}\]”>
\(\frac{4}{3}\prod \times r^{3}\]”>
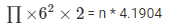
N= 16
= 16
16 spherical balls are required to raise the water level by 2 cm.
Question 31: The metallic spheres each of radius 2 cm area packed into a rectangular box of internal dimension 16 cm* 8cm* 8cm where 16 spheres are packed the box is filled with preservation liquid . Find the volume of this liquid ?
Solution:
Given,
Radius of the metallic spheres = 2 cm
Volume of the sphere 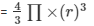
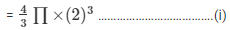
Total volume of the 16 spheres 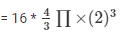
Volume of the rectangular box= 16*8*8 cm³³………………………………………(ii)
Subtracting equation (ii) from (i) we get the volume of the liquid
Volume of the liquid = (1024 – 536.16) cm³ =488 cm³
The volume of the liquid is 488 cm³
Question 32: A vessel in the shape of a cuboids’ contains some water. If 3 identical spheres are immersed in the water, the level of water is increased by 2 cm. If the area of the base of the cuboids is 160 cm2 and its height is 12 cm. determine the radius of any of the spheres?
Solution:
Given,
The area of the cuboids’= 160 cm2
Level of water in the vessel increased = 2 cm
Volume of the vessel = 160 *2 cm2
=320 cm2 ……………………………….. (i)
Volume of each sphere 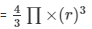
Total volume of 3 spheres = 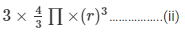
Now equating equation (i) and (ii) we get
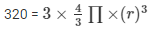
R= 2.94 cm.
The radius of the sphere so obtained is 2.94 cm.
Question 33: Water in a canal 1.5 m wide and 6 m deep is flowing with a sped of 10 km / hr .How much area will it irrigate in 30 minutes if 8 cm of standing water is desired?
Solution:
Given
Water is flowing at a speed of = 10 km / hr
In 20 minutes length of the flowing standing water = 10*30/60 = 5 km = 5000 m
Width of the canal = 1.5m
Depth of the canal = 6m
Volume of water in 20 minutes = 5000 * width * depth = 45000 m³
Irrigated area in 20 minutes if 5 cm of standing water is desired = 45000 / 0.08 m2 = 562500 m2
Irrigated area in 30 minutes is 562500 m2
Question 34: A tent of height 77 dm is in the form of aright angled circular cylinder of diameter 36 m and height 44 dm surmounted by a right circular cone. Find the cost of canvas at the rate of Rs.3.5 per m2.
Solution:
Given
The height of the tent = 77 dm
Height of the cone = 44 dm
Height of the tent without the cone = (77 – 44) dm = 33 dm
= 3.3 m
Diameter of the cylinder = 36 m
Radius of the cylinder = 36 / 2 m = 18 m
Let us assume the slant height of the cone be (l)
L2 = r2 + h2
L2 = (18)2 + (3.3)2
l =18.3 m
The slant height of the cone is 18.3 m.
Curved surface area of the cylinder = 2πrh
= 2 *π * 18*4.4 m2 ……………….. (i)
Curved surface area of the cone = πrh
= π * 18* 18.3 m2…………………….. (ii)
Now adding equation (i) and (ii) we will get the value of the total surface area
Total surface area = 1532.46 m2
Cost of canvas = 1532.46 m2 * Rs 3.5 = Rs 5363.61
Question 35: The largest sphere is to be curved out of a right circular cylinder of radius 7 cm and height 14 cm. find the volume of the sphere.
Solution:
Given radius of the cylinder = 7 cm
Height of the cylinder = 14 cm
Largest sphere is curved out from the cylinder.
Thus the diameter of sphere = diameter of cylinder
Diameter of the sphere = 2*7 = 14 cm
Volume of the sphere 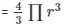
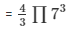
= 1436.75 cm³
Volume of the sphere is 1436.75 cm³
Question 36: A right angled triangle whose sides are 3cm, 4cm and 5 cm is revolved about the sides containing the right angle in two ways. Find the difference in volumes of the two cones so formed. Also find the curved surfaces?
Solution:
Given:
I>
Radius of the cone = 4 cm
Height of the cone = 3 cm
Slant height of the cone = 5 cm
Volume of the cone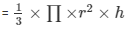
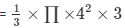
= 16π cm³
II>
Radius of the second cone = 3 cm
Height of the cone = 4 cm
Slant height of the cone = 5 cm
Volume of the cone 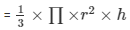
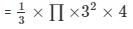
=12π cm³
Difference of the volumes of two cone = (16-12) πcm³
=4π cm³
Curved surface area of the first cone = π r1 l1
= π * 4 * 5 cm2
=20π cm2
Curved surface area of the second cone = π r2 l2
=π * 3 * 5 cm2 =15π cm2
Question 37: The volume of the hemisphere is 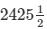 . find it’s curved surface area.
. find it’s curved surface area.
Solution:
Given,
Volume of the hemisphere 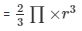
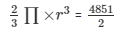
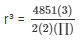
r = (1193.18) ⅓
r = 10.5 cm
Curved surface area of the hemisphere = 2πr2
2 * π *(10.5)2 = 693 cm2
The curved surface area of the hemisphere is 693 cm2.
Question 38: The difference between the outer and inner curved surface areas of a hollow right circular cylinder 14 cm long is 88 cm2. If the volume of metal used in making cylinder is 176 cm3. Find the outer and inner diameters of the cylinder?
Solution:
Given,
Height of the cylinder = 14 cm
Let the inner and outer radii of the hollow sphere be (r) and (R) respectively.
The difference between inner and outer curved surface area is 88 cm 2
Curved surface area of the hollow sphere = 2π(R-r) h
88 = 2π(R-r) h
88 = 2π(R-r) 14
R-r = 1 ………………………………….. (i)
Volume of the hollow cylinder 
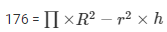
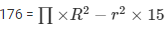
From equation (i) substituting the values of equation. We get,
R+ r = 4……………………………………. (ii)
Now solving both the equations we get,
2R= 5
R= 2.5cm & r = 1.5 cm
Inner radius of the hollow cylinder = 1.5 cm
Inner diameter of the hollow cylinder = 2 * 1.5 cm = 3 cm
Outer radius of the hollow cylinder = 2.5 cm
Outer diameter of the hollow cylinder = 5 cm
Question 39: The internal and external diameters of a hollow hemispherical vessel are 21 cm and 25.2 cm .The cost of painting 1 cm2 of the surface is 10 paisa. Find the total cost to paint the vessel all over.
Solution
Given,
Internal diameter of the hollow hemisphere = 21 cm
Internal radius of the hollow hemisphere = 21/2 = 10.5 cm
External diameter of the hollow hemisphere = 25.2 cm
External radius of the hollow hemisphere = 25.2/2 =12.6 cm
Total area of the hollow hemisphere 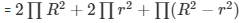
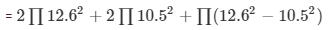
= 997.51+692.72 +152.39 cm2
=1843.38 cm2
According to the question,
The cost of painting of 1 cm2 of the surface is =10 p =Rs0.01
Then the total cost of painting = 1848.38 * 0.10
=Rs184.338
The total cost of painting all over the vessel is Rs.184.338.
Question 40: The difference between outer and inner curved surface area of a hollow right circular cylinder is 14cm long is 88 cm2. If the volume of metal used in making cylinder is 176 cm³. Find the outer and inner diameters of the cylinder?
Solution
Given,
Height of the hollow cylinder = 14 cm
Let the internal and external diameters of the hollow cylinder be r and R respectively.
Given that the difference between inner and outer curved surface =88 cm3
Curved surface area of a hollow cylinder = 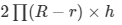
88=2π(R-r)* h
88=2*3.1428*(R-r)*14
R-r =1 …………………………..(i)
Volume of the hollow cylinder 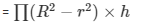
Volume of the hollow cylinder= 176cm³
π (R2-r2) h =176
R2-r2 = 4
R+ r = 4 …………………………..(ii)
Now, solving eq I and ii we get,
R-r = 1
R+ r = 4
2R = 5
R=2.5 cm
r = 1.5 cm
The internal and external radii of the hollow cylinder are 1.5 cm and 2.5 cm respectively.
Question 41: Prove that the surface area of a sphere is equal to the curved surface area of the circumscribed cylinder.
Solution:
Let the radius of the sphere be (r)
Curved surface area of the sphere =4πr2 ……………………….. (i)
S1 = 4πr2
Let the radius of the cylinder be (r)
Let the height of the cylinder be (2r)
Curved surface area of the cylinder = 2πrh
S2= = 2πr (2r)
=4πr2 …………………………………….. (ii)
From the above equations, it is proven that surface area of the sphere is equal to the curved surface area of the circumscribed cylinder.
FAQs on Surface Area and Volume Exercise 16.1(Part-2) - Class 10
| 1. What is the formula for calculating the surface area of a rectangular prism? |  |
| 2. How do you find the surface area of a cone? |  |
| 3. What is the volume of a cylinder? |  |
| 4. How do you find the volume of a sphere? |  |
| 5. How do you calculate the surface area of a triangular prism? |  |


















