Some Applications of Trigonometry Exercise 12.1(part-2) - Class 10 PDF Download
Q24.A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, angle of elevation of the top of the statue is 60∘ and from the same point the angle of elevation of the top of the pedestal is 45∘. Find the height of the pedestal.
Soln:
let the height of the pedestal be ‘h’ m
Height of the statue = 1.6 m
Angle of elevation of the top of the statue α=30∘
Angle of elevation of the top of the pedestal β=30∘
The above data is represented in the form of figure as shown.
If in right angle triangle one of the included angle is Θ
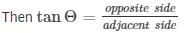
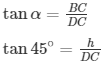
DC = ‘h’ m —- (a)
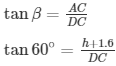
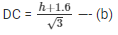
From (a) and (b)
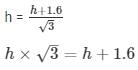
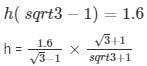
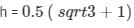
Height of the pedestal 
Q25.A T.V. tower stands vertically on a bank of a river of a river. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60∘. From a point 20 m away this point on the same bank, the angle of elevation of the top of the tower is 30∘. Find the height of the tower and the width of the river.
Soln:
let AB be the T.V tower of height ‘h’ m on the bank of river and ‘D’ be the point on the opposite side of the river. An angle of elevation at the top of the tower is 300
Let AB = h and BC = x
Here we have to find height and width of the river.
The above data is represented in the form of figure as shown.
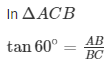
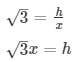
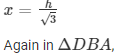
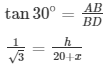
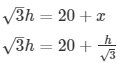
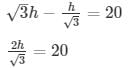
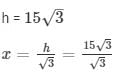
x = 10
Hence the height of the tower is 10√3m and width if the river is 10 m .
Q26.From the top of a 7 m high building, the angle of elevation of the top of a cable is 60∘ and the angel of depression of its foot is 45∘. Determine the height of the tower.
Soln:
Given
Height of the building = 7 m = AB
Height of the cable tower = ‘H’ m = CD
Angle of elevation of the top of the building α=60∘
Angle of elevation of the bottom of the building β=45∘
The above data is represented in form of figure as shown
Let CX = ‘x’ m
CD = DX + XC = 7 m +’x’ m
= x + 7m
In ΔADX
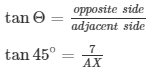
AX = 7m
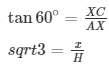
x = 7sqrt3
But CD = x + 7
= 7sqrt3+7
=7(sqrt3+1)m
Height of the cable tower = =7(sqrt3+1)m
Q27.As observed from the top of a 75 m tall lighthouse, the angles of depression of two ships are 30∘ and 45∘. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Soln:
Given;
Height of the lighthouse = 75m = ‘h’ m = AB
Angle of depression of ship 1, α=30∘
Angle of depression of bottom of the tall building, β=45∘
The above data is represented in form of figure as shown
Let distance between ships be ‘x’ m = CD
If in right angle triangle one of the included angle is Θ
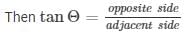
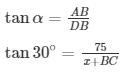
x + BC = 75sqrt3....(1)
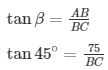
BC = 75 —- (2)
Substituting (2) in (1)
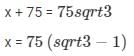
distance between ships = xm
x = 75 (sqrt3-1)
Q28.The angle of elevation of the top of the building from the foot of the tower is 30∘ and the angle of the top of the tower from the foot of the building is 60∘. If the tower is 50m high, find the height of the building.
Soln:
Angle of elevation of top of the building from foot of tower =30∘=α
Angle of elevation of top of the building from foot of tower =60∘=β
Height of the tower = 50m = AB
Height of building = ‘h’ m =CD
The above data is represented in the form of figure as shown
In right triangle if one of the included angle is Θ
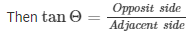
In ΔABD
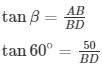
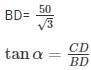
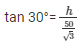
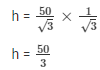
height of the building = 50/3 m
Q29.From a point on a bridge across a river the angle of depression of the banks on opposite side of the river are 30∘ and 45∘ respectively. If the bridge is at the height of 30m from the banks, find the width of the river.
Soln:
Height of the bridge = 30m [AB]
Angle of depression of bank 1 i.e, α=30∘B1
Angle of depression of bank 2 i.e, β=30∘B2
Given banks are on opposite sides
Distance between banks B1B2=BB1+BB2
The above data is represented in the form of figure as shown
In right angle triangle, if one of the included angle is Θ
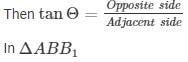
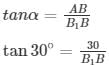
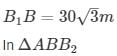
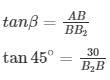
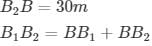
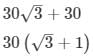
Distance between banks = 30 (√3+1)m
Q30.A man sitting at a height of 20 m on a tall tree on a small island in the middle of a river observes two poles directly opposite to each other on the two banks of the river and in line with foot of tree. If the angles of depression of the feet of the poles from a point at which the man is sitting on the tree on either side of the river are 60∘ and 30∘ respectively. Find the width of the river.
Soln:
Height of the tree AB = 20m
Angle of depression of the pole 1 feet α=60∘B1
Angle of depression of the pole 2 feet β=30∘B1
B1C1 be one pole and B2C2 be the other pole
Given poles are on opposite sides.
Width of the river = B1B2
= B1B+BB2
The above data is represented in the form of figure as shown
In right angle triangle, if one of the included angle is Θ

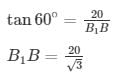
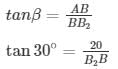
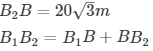
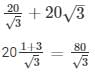
Width of the river = 80/√3 m
Q31.A vertical tower stands on a horizontal plane and is surmounted by a flag staff of height 7m. From a point on the plane, the angle of elevation of the bottom of flag staff is 30∘ and that of the top of the flag staff is 45∘. Find the height of the tower.
Soln:
Given
Height of the flag staff = 7m = BC
Let height of the tower = ‘h’ m = AB
Angle of elevation of top of the bottom of the flagstaff α=30∘
Angle of elevation of top of the top of the flagstaff β=45∘
Points of desecration be ‘p’
The above data is represented in the form of figure as shown
In right angle triangle, if one of the included angle is Θ
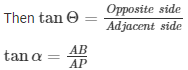
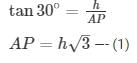

AP = h + 7 —- (2)
From (1) and (2)
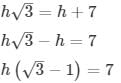

h = 3.5 ( √3+1 )m
height of tower = 3.5 ( √3+1 )m.
Q32.The length of the shadow of a tower standing on level plane is found to be 2x meters longer when the sun’s attitude is 30∘ than when it was 30∘. Prove that the height of tower is x(√3+1)meters.
Soln:
Let
Length of shadow be ‘a’ m [BC] when sun altitude be α=45∘
Length of shadow be (2x+a) m [BD] when sun altitude be β=30∘
Let height of tower be ‘h’ m =AB
The above data is represented in the form of figure as shown
In right angle triangle one of the included angle is Θ

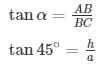
h = a —- (1)
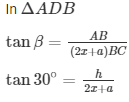
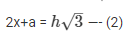
Substituting (1) in (2)
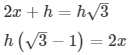
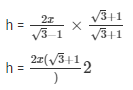
h = x√3+1)
height of tower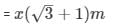
Q33.A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle of 30∘ with the ground. The distance from the foot of the tree to the point where the top touches the ground is 10 meters. Find the height of the tree.
Soln:
Let AB be the height of the tree and it is broken at point C and top touches ground at B’
Angle made by the top α=30∘
Distance from foot of tree from point where it touches ground = 10 m
The above data is represented in form of figure as shown
Height of the tree = AB = AC + CB
= AC + CB’
In right angle triangle one of the included angle is Θ
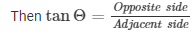
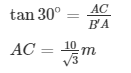
Again
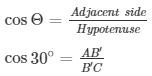
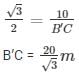
AB = CA + CB’
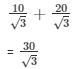
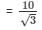
Height of tree = 10/√3 m
Q34.A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 60∘ to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
Soln:
Length of the cable connected to balloon = 215m [CB]
Angle of inclination of cable with ground α=60∘
Height of the balloon from ground = ‘h’ m = AB
The above data is represented in from of figure as shown
In right angle triangle one of the included angle is Θ
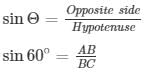
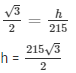
h = 107.5√3 m
Height of the ballon from ground = 107.5√3 m
Q35. Two men on either side of the cliff 80m high observe the angles of elevation of the top of the cliff to be 300 and 600 respectively. Find the distance between the two men.
Soln:
Height of cliff = 80m = AB
Angle of elevation from Man 1, α=30∘[M1]
Angle of elevation from Man 2, β=60∘[M2]
Distance between two men = M1M2=BM1+BM2
The above information is represented in form of figure as shown
In right angle triangle one of the included angle is Θ
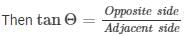
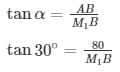
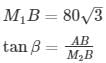
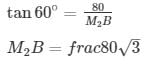
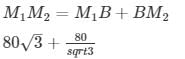
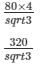
Distance between men = 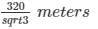
Q36.Find the angle of elevation of the sun (sun’s altitude) when the length of the shadow of a vertical pole is equal to its height.
Soln:
Let
Height of the pole = ‘h’ m =sun’s altitude from ground length of shadow be ‘L’
Given that L = h.
Angle of elevation of sun’s altitude be Θ
The above data is represented in from of figure as shown
In right angle triangle one of the included angle is Θ
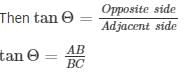
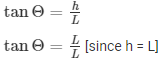
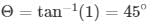
Angle of sun’s altitude is 450
Q37.A man standing is on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60∘ and the angle of depression of the base of the hill as 30∘. Calculate the distance of the hill from the ship and the height of the hill.
Soln:
Height of the ship above water level = 8m = AB
Angle of elevation of top of cliff (hill) α=60∘
Angle of depression of the bottom of hill β=30∘
Height of the hill = CD
Distance between ship and hill = AX
Height of the hill above ship = CX = ‘a’ m
Height of hill = (a + 8) m
The above data is represented in form of figure as shown
In right angle triangle if one of the included angle is Θ
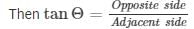
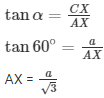
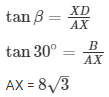
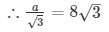
a = 24m
AX = 8√3m
Height of the cliff hill = (24+8) m = 32m
Distance between hill and ship 8√3m
Q38.The angles of depression of two ships from the top of a light house and on the same side of it are found to be 45∘ and 30∘ respectively. If the ships are 200 m apart, find the height of the light house.
Soln:
Height of the light house AB = ‘h’ meters
Let S1andS2 be ships
Distance between ships S1S2=200m
Angle of depression of S1(α=30∘)
Angle of depression of S2(β=45∘)
The above data is represented in form of form of figure as shown
In ΔABS2
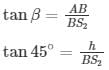
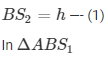
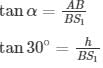
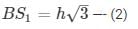
Subtracting (1) from (2)
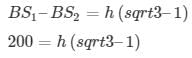
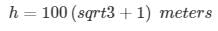
Height of the light house = 273.2 meters
Q39.The angles of elevation from the top of a tower from two points at distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.
Soln:
Height of the tower AB = ‘h’ meters
Let point C be 4 meters from B.
Angle of elevation is α given point D is 9 meters from B, Angle of elevation is β
Given α, β are complementary, α + β=90∘=>=;β=90∘α
Required to prove that h = 6 meters
The above data is represented in the form of figure as shown
In ΔABC
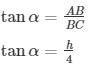
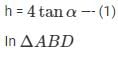
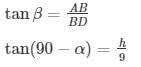
h = 9 tan α....(2)
Multiply (1) and (2)
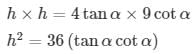
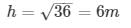
Height of tower = 6 meters
FAQs on Some Applications of Trigonometry Exercise 12.1(part-2) - Class 10
| 1. What are some real-life applications of trigonometry? |  |
| 2. How is trigonometry used in the field of engineering? |  |
| 3. Can you provide an example of how trigonometry is used in navigation? |  |
| 4. How does trigonometry help in solving problems related to waves and vibrations? |  |
| 5. What role does trigonometry play in architecture and construction? |  |














