Single Slit Experiment & Diffraction Pattern | Physics for JEE Main & Advanced PDF Download
Single Slit Interference
- Light passing through a single slit forms a diffraction pattern somewhat different from those formed by double slits or diffraction gratings. shows a single slit diffraction pattern.
- Note that the central maximum is larger than those on either side, and that the intensity decreases rapidly on either side. In contrast, a diffraction grating produces evenly spaced lines that dim slowly on either side of center.
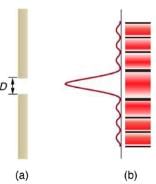
- (a) Single slit diffraction pattern. Monochromatic light passing through a single slit has a central maximum and many smaller and dimmer maxima on either side. The central maximum is six times higher than shown. (b) The drawing shows the bright central maximum and dimmer and thinner maxima on either side.
 Single Slit Interference
Single Slit Interference
- The analysis of single slit diffraction is illustrated in. Here we consider light coming from different parts of the same slit. According to Huygens’s principle, every part of the wavefront in the slit emits wavelets. These are like rays that start out in phase and head in all directions. (Each ray is perpendicular to the wavefront of a wavelet.) Assuming the screen is very far away compared with the size of the slit, rays heading toward a common destination are nearly parallel.
- When they travel straight ahead, as in (a), they remain in phase, and a central maximum is obtained. However, when rays travel at an angle θ relative to the original direction of the beam, each travels a different distance to a common location, and they can arrive in or out of phase.
- In (b), the ray from the bottom travels a distance of one wavelength λ farther than the ray from the top. Thus a ray from the center travels a distance D farther than the one on the left, arrives out of phase, and interferes destructively. A ray from slightly above the center and one from slightly above the bottom will also cancel one another.
- In fact, each ray from the slit will have another to interfere destructively, and a minimum in intensity will occur at this angle. There will be another minimum at the same angle to the right of the incident direction of the light.
- Light passing through a single slit is diffracted in all directions and may interfere constructively or destructively, depending on the angle. The difference in path length for rays from either side of the slit is seen to be
 .
.




At the larger angle shown in , the path lengths differ by  for rays from the top and bottom of the slit. One ray travels a distance D different from the ray from the bottom and arrives in phase, interfering constructively.
for rays from the top and bottom of the slit. One ray travels a distance D different from the ray from the bottom and arrives in phase, interfering constructively.
- Two rays, each from slightly above those two, will also add constructively. Most rays from the slit will have another to interfere with constructively, and a maximum in intensity will occur at this angle. However, all rays do not interfere constructively for this situation, and so the maximum is not as intense as the central maximum.
- Finally, in the angle shown is large enough to produce a second minimum. As seen in the figure, the difference in path length for rays from either side of the slit is
 , and we see that a destructive minimum is obtained when this distance is an integral multiple of the wavelength.
, and we see that a destructive minimum is obtained when this distance is an integral multiple of the wavelength. - A graph of single slit diffraction intensity showing the central maximum to be wider and much more intense than those to the sides. In fact the central maximum is six times higher than shown here.

- Thus, to obtain destructive interference for a single slit,

- where D is the slit width, λ is the light’s wavelength, θ is the angle relative to the original direction of the light, and m is the order of the minimum. shows a graph of intensity for single slit interference, and it is apparent that the maxima on either side of the central maximum are much less intense and not as wide. This is consistent with the illustration in (b).
Calculating Single Slit Diffraction
Ex. Visible light of wavelength 550 nm falls on a single slit and produces its second diffraction minimum at an angle of 45º relative to the incident direction of the light.
(a) What is the width of the slit?
(b) At what angle is the first minimum produced?
A graph of the single slit diffraction pattern is analyzed in this example.
Strategy
From the given information, and assuming the screen is far away from the slit, we can use the equation Dsin θ = m first to find D, and again to find the angle for the first minimum θ1.
Solution for (a)
We are given that λ = 550 nm, m = 2 and θ2 = 45.0. Solving the equation Dsin θ = m for D and substituting known values gives
Solution for (b)
Solving the equation D sin θ= m for sin θ1 and substituting the known values gives
Thus the angle θ1 is
Diffraction
The bending of light waves around the corners of an obstacle or aperture is called diffraction of light.
The phenomenon of diffraction is divided mainly in the following two classes
(a) Fresnel class
(b) Fraunhofer class
| S.No | Fresnel Class | Fraunhofer Class |
| 1 | The source is at a finite distance | The source is at infinite distance |
| 2 | No opticals are required. | Opticals are in the form of Collimating lens and focusing lens are required. |
| 3 | Fringes are not sharp and well defined. | Fringes are sharpend well defined. |
Fraunhofer Diffraction at a Single Slit
Linear Width 0f central maximum 2Dλ / a = 2fλ / a
Angular width of central maximum = 2λ / a
where, λ = wavelength of light, a = width of single slit, D = distance of screen from the slit and f = focal length of convex lens.
For Secondary Minima
(a) Path difference = nλ
(b) Linear distance = nDλ / a = nfλ / a
(c) Angular spread = nλ / a
where, n = 1, 2, 3,.,.
For Secondary Maxima
(a) Path difference = (2n + 1) λ/ 2
(b) Linear distance = (2n + 1) Dλ / 2a = (2n + 1) fλ / 2a
(c) Angular spread = (2n + 1) λ / 2
Important Points
- A soap bubble or oil film on water appears coloured in white light due to interference of light reflected from upper and lower surfaces of soap bubble or oil film.
- In interference fringe pattern all bright and dark fringes are of same width,
- In diffraction fringe pattern central bright fringe is brightest and widest. and I remaining secondary maxima's are of gradually decreasing intensities.
- The difference between interference and diffraction is that the interference is the superposition between the wavelets coming from two coherent sources while the diffraction is the superposition between the wavelets coming from the single wavefront.
|
268 videos|780 docs|209 tests
|
FAQs on Single Slit Experiment & Diffraction Pattern - Physics for JEE Main & Advanced
| 1. What is the single slit interference phenomenon? |  |
| 2. How does the diffraction single slit experiment work? |  |
| 3. What factors affect the diffraction pattern in a single slit experiment? |  |
| 4. How can the intensity of the fringes in a single slit diffraction pattern be explained? |  |
| 5. What is the significance of studying single slit interference and diffraction patterns? |  |
















