Cartesian Product of Two Sets | Mathematics (Maths) Class 12 - JEE PDF Download
Cartesian Product of Sets
Before getting familiar with this term, let us understand what does Cartesian mean. Remember the terms used when plotting a graph paper like axes (x-axis, y-axis), origin etc. For example, (2, 3) depicts that the value on the x-plane (axis) is 2 and that for y is 3 which is not the same as (3, 2).
The way of representation is fixed that the value of the x coordinate will come first and then that for y (ordered way). Cartesian product means the product of the elements say x and y in an ordered way.
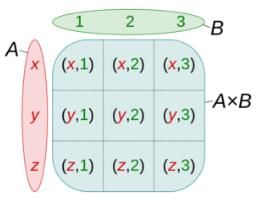
Cartesian Product of Sets
The Cartesian products of sets mean the product of two non-empty sets in an ordered way. Or, in other words, the collection of all ordered pairs obtained by the product of two non-empty sets. An ordered pair means that two elements are taken from each set.
For two non-empty sets (say A & B), the first element of the pair is from one set A and the second element is taken from the second set B. The collection of all such pairs gives us a Cartesian product.
The Cartesian product of two non-empty sets A and B is denoted by A × B. Also, known as the cross-product or the product set of A and B. The ordered pairs (a, b) is such that a ∈ A and b ∈ B. So, A × B = {(a,b): a ∈ A, b ∈ B}. For example, Consider two non-empty sets A = {a1, a2, a3} and B = {b1, b2, b3}
Cartesian product A×B = {(a1, b1), (a1, b2), (a1, b3), ( a2, b1), (a2, b2),(a2, b3), (a3, b1), (a3, b2), (a3, b3)}.
It is interesting to know that (a1, b1) will be different from (b1, a1). If either of the two sets is a null set, i.e., either A = Φ or B = Φ, then, A × B = Φ i.e., A × B will also be a null set
Number of Ordered Pairs
For two non-empty sets, A and B. If the number of elements of A is h i.e., n(A) = h & that of B is k i.e., n(B) = k, then the number of ordered pairs in Cartesian product will be n(A × B) = n(A) × n(B) = hk.
Solved Example
Q.1. Let P & Q be two sets such that n(P) = 4 and n(Q) = 2. If in the Cartesian product we have (m, 1), (n, -1), (x, 1), (y, -1). Find P and Q, where m, n, x, and y are all distinct.
Solution. P = Set of first elements = {m, n, x, y} and Q = Set of second elements = {1, -1}
|
203 videos|307 docs|139 tests
|
FAQs on Cartesian Product of Two Sets - Mathematics (Maths) Class 12 - JEE
| 1. What is the Cartesian product of two sets? |  |
| 2. How do you calculate the Cartesian product of two sets? |  |
| 3. What is the cardinality of the Cartesian product of two sets? |  |
| 4. Can the Cartesian product of two sets be empty? |  |
| 5. How is the Cartesian product related to combinatorics? |  |
















