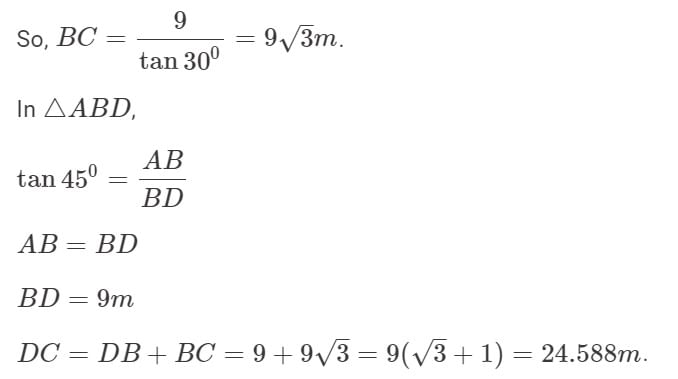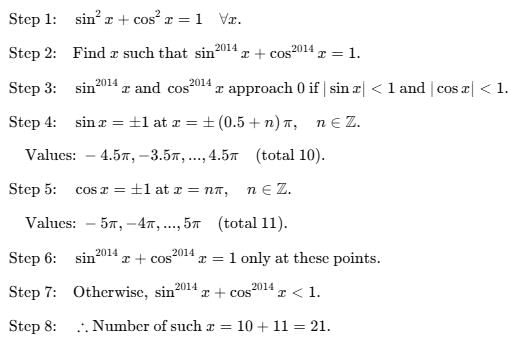Basic Concepts: Trigonometry | Quantitative Aptitude (Quant) - CAT PDF Download
| Table of contents |

|
| What is Trigonometry? |

|
| Trigonometric Ratios of Specific Angles |

|
| Basic Trigonometric Identities |

|
| Application of Trigonometry - Heights and Distances |

|
| Solved Examples |

|
Trigonometry is a key topic in many entrance exams' Quantitative Aptitude section, often appearing in problems involving heights and distances, geometry, and data interpretation. Mastering these concepts can help you solve complex problems efficiently, saving valuable time during the exam. This document aims to simplify trigonometry for your preparation with clear explanations, examples, and practice questions.

What is Trigonometry?
Trigonometry is the branch of mathematics that deals with the study of relationships between sides and angles of a triangle. It is derived from the Greek word 'Trigonon' and 'metron' where , Tri meaning three and Gon means Angle and Metron means Measure.
- A trigonometric ratio is defined as the ratio of the lengths of two sides in a right-angled triangle, forming the foundation of trigonometry.
- These ratios, also known as trigonometric functions, are essential tools for analysing relationships between angles and sides.
- There are six fundamental trigonometric ratios, with sine, cosine, and tangent being the most widely used, abbreviated as sin, cos, and tan, respectively.
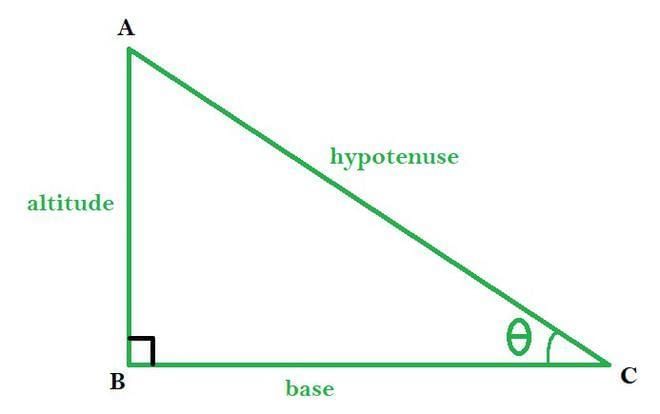
To understand these ratios, consider a right-angled triangle ABC with ∠B = 90°. The longest side, AC, is called the hypotenuse. Relative to ∠A, the side AB is the adjacent side (next to ∠A), and the side BC is the opposite side (across from ∠A).
- AC = Hypotenuse of the triangle
- AB =Altitude of the triangle
- BC = Base of the triangle
Quick Reference Formula Sheet
Trigonometric Ratios:

Identities:

Special Triangles:
- 45-45-90: 1 : 1 : √2
- 30-60-90: 1 : √3 : 2
Trigonometric Ratios of Specific Angles
- The values of sin, cos, and tan for 0°, 30°, 45°, 60°, and 90° can be derived using special triangles.
- For a 30-60-90 triangle with sides 1:√3:2, sin 30° = 1/2 (opposite/hypotenuse).
- For a 45-45-90 triangle with sides 1:1:√2, sin 45° = 1/√2.
- To memorise, note the pattern for sin θ: √0/2, √1/2, √2/2, √3/2, √4/2.
Table: Trigonometric Ratios of Specific Angles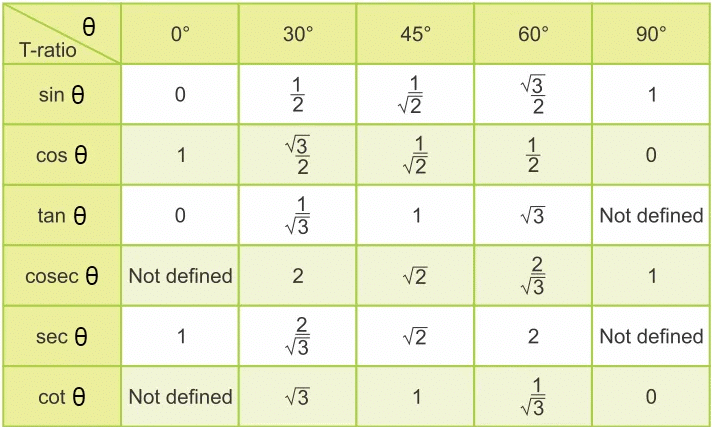
- Two angles are said to be complementary if their sum is 90°. Thus ϴ and (90 – ϴ) are complementary angles.
- Representing complementary angles in terms of these standard angles helps in solving a complex problem involving trigonometric ratios.
Trigonometric Ratios of Complementary Angles

Basic Trigonometric Identities
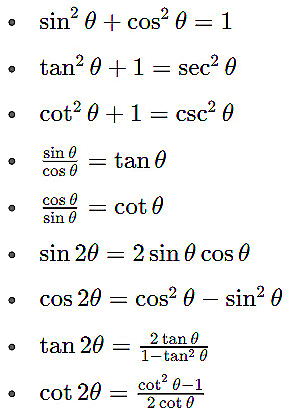
Note:
1. The identity sin² θ + cos² θ = 1 comes from the Pythagorean theorem.
In a right triangle, (opposite)² + (adjacent)² = (hypotenuse)². Dividing through by (hypotenuse)², we get (opposite/hypotenuse)² + (adjacent/hypotenuse)² = 1, which is sin² θ + cos² θ = 1.
2. The identity sin 2θ = 2 sin θ cos θ can be derived from the sum identity sin(u + v) = sin u cos v + cos u sin v by setting u = θ and v = θ.
Sum and Difference Identities
For angles u and v, we have the following relationships:

Value change with change of angle by π/2 or π or negative sign
When the angle of θ is changed by π/2 or by π the va\lues of the trigonometric functions change in simple ways.
1. Change by π/2:

2. Change by π:
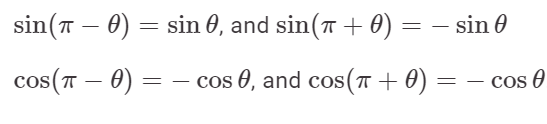
3. Change by Sign:
sin(−θ) = −sinθ, and cos(−θ)=cosθ.
Two Special Triangles
- There are two special triangles we need to know 45°-45°-90° and 30°-60°-90° triangles.
They are depicted in the figures below.
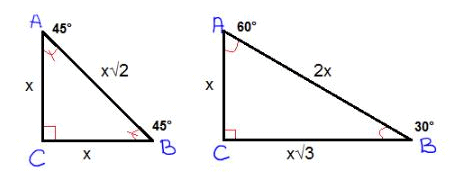
- The figures show how to find the side lengths of those types of these special triangles.
- In a 45-45-90 triangle ABC shown above, ratio of side AC:BC:AB = 1 :1 : 1/√2
- In a 60-30-90 triangle ABC shown above, ratio of sides AC:BC:AB = 1 : 1/√3 : 2
Application of Trigonometry - Heights and Distances
In this problem area, an object stands upright perpendicularly on the surface and from a distance, the object is observed. If the angle of elevation is known along with one of the height or distance to the object, the other can be determined.
1. Angle of Elevation
When the observer looks up to the top of a tall object, the angle made by the horizontal line through the point of observation and the line from the top of the object to the point of observation is the angle of elevation.
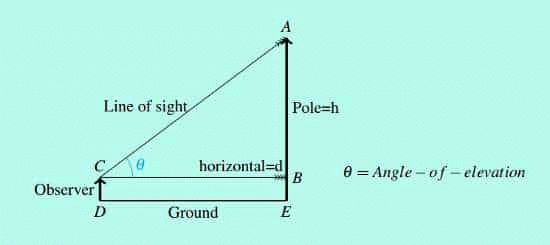
We have here, h/d= tanθ.
For Example,
Imagine you’re standing on the ground, looking up at the top of a flagpole in your school courtyard.
If you’re 10 meters away from the base of the flagpole and the angle you make with the ground while looking at the top is 30°, this angle is the angle of elevation.
Using trigonometry, you can calculate the height of the flagpole!
Example: A person standing 20 meters away from the base of a tree observes the top of the tree at an angle of elevation of 45°. What is the height of the tree?
Sol: Let the height of the tree be h meters.
In the right triangle formed,
tan 45° = h/20.
Since tan 45° = 1,
We have h/20 = 1, so h = 20 meters.
Thus, the height of the tree is 20 meters.
2. Angle of Depression
When an observer looks down from the top of a tall object, we get the angle of depression.
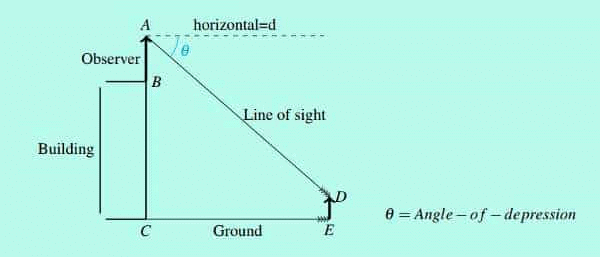
Example: From a point A on the bridge over a river, the angles of depression of the banks on the opposite sides of the river are 30º and 45º, respectively. If the bridge is at a height of 9m above the river surface, find how wide the river is.
The width of the river is DC. In triangle △ABC, tan 30º= AB/BC300
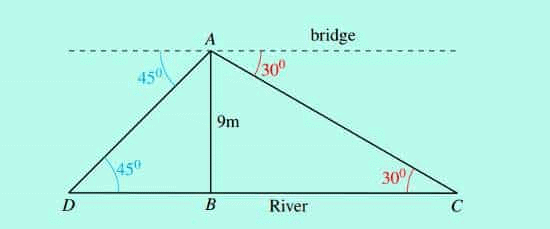
Solution:
Solved Examples
The following examples are categorised by type to help you practice systematically. Start with heights and distances, then move to identities and geometry problems.
Tip: For heights and distances, always draw a diagram and identify whether to use tan, sin, or cos based on the given sides and angles.
Example 1: Anil looked up at the top of a lighthouse from his boat and found the angle of elevation to be 30º. After sailing in a straight line 50 m towards the lighthouse, he found that the angle of elevation changed to 45º. Find the height of the lighthouse.
a. 25
b. 25√3
c. 25(√3-1)
d. 25(√3+1)
Ans: Option (d)
Sol:
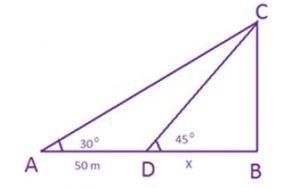
Example 2: An aeroplane when flying at the height of 3125 m from the ground passes vertically below another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 30º and 60º, respectively. Find the distance between the two planes at that instant.
Sol:
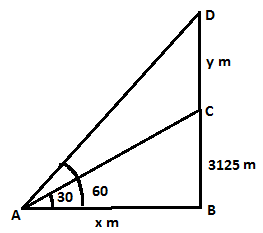
Example 3: An airplane flying at 3000 m above the ground passes vertically above another plane at an instant when the angle of elevation of the two planes from the same point on the ground are 60º and 45º respectively. The height of the lower plane from the ground is:
a. 1000√3 m
b. 1000/√3 m
c. 500 m
d. 1500(√3+1)
Ans: Option (b) is correct.
Sol:
Let the higher plane fly such that at point A the angle of elevation from point D is 60º.
Let the height of the plane flying at a lower level be CD = y (since tan 45º= 1)
⇨ tan 60º = 3000/y
⇨ √3 = 3000/y
⇨ y = 3000/√3 = 1000√3
Example 4: What is the value of (1-CosA) / (1+CosA) given that tan A = ¾?
a. 1/4
b. 9/16
c. 1/9
d. 1/3
Ans: Option (c) is correct.
Sol:
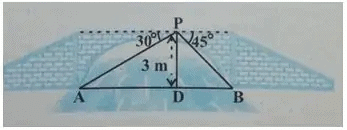
Example 5: From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30 degree and 45 degree respectively. If the bridge is at a height of 3 m from the banks, find the width of the river.
Sol: In the below figure, A and B represent points on the bank on the opposite sides of the river. P is a point on the bridge at a height of 3 m. Length of the side AB is the width of the river.
Now, AB = AD + DB
In right Δ APD, angle A = 30°
So, tan 30° = PD / AD
Or 1/ √3 = 3 / AD or AD = 3√3 m
Also, In right Δ PBD, angle B = 45°. So, BD = PD = 3 m
Now, AB = BD + AD = 3 + 3√3 m
Example 6: 3sinx + 4cosx + r is always greater than or equal to 0. What is the smallest value ‘r’ can take?
a. 5
b. -5
c. 4
d. 3
Ans: Option (a) is correct.
Sol: 3sinx + 4cosx ≥ -r
5(3/5sinx + 4/5cosx) ≥ -r
3/5 = cosA => sinA =4/5
5(sinx cosA + sinA cosx) ≥ -r
5(sin(x + A)) ≥ -r
5sin (x + A) ≥ -r
-1 ≤ sin (angle) ≤ 1
5sin (x + A) ≥ -5
rmin = 5
Example 7: Sin2014x + Cos2014x = 1, x in the range of [-5π, 5π], how many values can x take?
a. 0
b. 10
c. 21
d. 11
Ans: Option (c) is correct.
Sol:
Example 8: Consider a regular hexagon ABCDEF. There are towers placed at B and D. The angle of elevation from A to the tower at B is 30 degrees, and to the top of the tower at D is 45 degrees. What is the ratio of the heights of towers at B and D?
a. 1:√3
b. 1:2√3
c. 1:2
d. 3:4√3
Ans: Option (b) is correct.
Sol: When you look at your reflection through a mirror, the image is at a distance equal to the distance between mirror and you. Now, think about what this has to with trigonometry.
Let the hexagon ABCDEF be of side ‘a’. Line AD = 2a. Let towers at B and D be B’B and D’D respectively.
Hence, the answer is 1:2√3
From the given data we know that ∠B´AB = 30° and ∠D´AB = 45°. Keep in mind that the Towers B’B and D´D are not in the same plane as the hexagon.In Triangle B’AB,
Tan∠B´AB = B´AB = B′B/AB = 1/3
=> B’B = a/√3
In Triangle D´AD, tan ∠D´AD = D′D/AD = 1
=> D’D = 2a
The ratio of heights = 1/√3 or 1/2√3
Answer choice (B)
Example 9: A man standing on top of a tower sees a car coming towards the tower. If it takes 20 minutes for the angle of depression to change from 30° to 60°, what is the time remaining for the car to reach the tower?
a. 20√3 minutes
b. 20 minutes
c. 10 minutes
d. 20√3 minutes
Ans: Option (c) is correct.
Sol:=> a + b = 3b
=> 2b = a
=> b = a2
Now since the car takes 20 minutes to travel a distance
Time taken to travel b =a/2 = = 10 minutes
Example 10: A student is standing with a banner at the top of a 100 m high college building. From a point on the ground, the angle of elevation of the top of the student is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the student.
a. 35m
b. 73.2m
c. 50m
d. 75m
Ans: Option (b) is correct.
Sol:
Let BC be the height of the tower and DC be the height of the student.
In rt. ∆ ABC
AB = BC cot 45°
AB = 100 m (i)
In rt. ∆ ABD
AB = BD cot 60°
AB = (BC + CD) cot 60°
AB = (10 + CD)*1/3 (ii)
Equating (i) and (ii)
(10 + CD) * 1/3 = 100
(10 + CD)= 100√3
CD = 100√3 – 100
= 10(1.732 – 1) = 100 * 0.732 = 73.2 m
Example 11: In a trapezium ABCD, AB is parallel to DC, BC is perpendicular to DC and ∠BAD = 45°. If DC = 5 cm, BC = 4 cm, the area of the trapezium in sq. cm is
a. 22 cm2
b. 29 cm2
c. 28 cm2
d. 32 cm2
Ans: Option (c) is correct.
Sol: Let us consider a trapezium
In ΔAED, ∠AED = 90°, ∠DAE = 45°,
therefore ∠EDA = 45°.
Clearly ΔAED is an isosceles right triangle and Quadrilateral BCDE is a rectangle.
Therefore, BC = DE = 4cm.
Since ΔAED is an isosceles triangle, AE = ED = 4cm.
Area of the Trapezium = Area of ΔAED + Area of Rectangle BCDE
Area of the Trapezium = 1/2 × AE × ED + DC × BC
Area of the Trapezium = 12 × 4 × 4 + 5 × 4
Area of the Trapezium = 8 + 20
Area of the Trapezium = 28 cm2
Common Mistakes and Time-Saving TipsMistakes to Avoid:
- Forgetting to check if tan θ is defined (e.g., tan 90° is undefined).
- Mixing up complementary angles (e.g., using sin(90° - θ) = sin θ instead of cos θ).
- Not simplifying expressions before substituting (e.g., simplify (1 - cos A)/(1 + cos A) first).
Tips:
- Memorise sin, cos, and tan values for standard angles to avoid calculations.
- For heights and distances, quickly label the triangle (opposite, adjacent, hypotenuse).
- Use approximations: √3 ≈ 1.732, √2 ≈ 1.414 for faster MCQ solving.
|
165 videos|229 docs|95 tests
|
FAQs on Basic Concepts: Trigonometry - Quantitative Aptitude (Quant) - CAT
| 1. What is the definition of Trigonometry? |  |
| 2. What are the trigonometric ratios for specific angles like 0°, 30°, 45°, 60°, and 90°? |  |
| 3. What are the basic trigonometric identities? |  |
| 4. How is trigonometry applied in calculating heights and distances? |  |
| 5. Can you provide an example of a common trigonometry problem related to heights and distances? |  |