Question with Answers: Pipes and Cistern - 1 | Quantitative Aptitude (Quant) - CAT PDF Download
Question 1: A drain pipe can drain a tank in 12 hours, and a fill pipe can fill the same tank in 6 hours. A total of n pipes – which include a few fill pipes and the remaining drain pipes – can fill the entire tank in 2 hours. How many of the following values could ‘n’ take?
a. 24
b. 16
c. 33
d. 13
e. 9
f. 8
(A) 3
(B) 4
(C) 2
(D) 1
Answer: A
Explanation:
Two drain pipes can drain the same volume that one fill pipe fills. This means that a D-D-F combination has to have a net volume effect of 0.
In spite of this, the tank still gets filled. Only the fill pipes can manage to fill the tank. In addition to all the net zero effect pipes, we need three more fill pipes in order to fill the tank in 2 hours.
So, we can have as many D-D-Fs as we want, but we need one F-F-F at the end to ensure that the tank gets filled in 2 hours.
So the number of pipes will be → (D – D - F).......(D – D - F) + (F – F - F).
The number of pipes has to be a multiple of 3. Only options (a), (c) and (e) fit the description.
The question is "How many of the following values could ‘n’ take?"
Hence, the answer is 3.
Question 2: Pipe A, B and C are kept open and together fill a tank in t minutes. Pipe A is kept open throughout, pipe B is kept open for the first 10 minutes and then closed. Two minutes after pipe B is closed, pipe C is opened and is kept open till the tank is full. Each pipe fills an equal share of the tank. Furthermore, it is known that if pipe A and B are kept open continuously, the tank would be filled completely in t minutes. How long will it take C alone to fill the tank ?
(A) 18
(B) 36
(C) 27
(D) 24
Answer: D
Explanation:
A is kept open for all t minutes and fills one-third the tank. Or, A should be able to fill the entire tank in '3t' minutes.
A and B together can fill the tank completely in t minutes. A alone can fill it in 3t minutes.
A and B together can fill 1/t of the tank in a minute. A alone can fill 1/3t of the tank in a minute. So, in a minute, B can fill 1/t - 1/3t = 2/3t. Or, B takes 3t/2 minutes to fill an entire tank.
To fill one-third the tank, B will take t/2 minutes. B is kept open for t - 10 minutes.
t/2 = t - 10, t = 20 minutes.
A takes 60 minutes to fill the entire tank, B takes 30 minutes to fill the entire tank. A is kept open for all 20 minutes. B is kept open for 10 minutes.
C, which is kept open for 8 minutes also fills one-third the tank. Or, C alone can fill the tank in 24 minutes.
The question is "Find the time taken by C to fill the tank?"
Hence, the answer is "24".
Question 3: Pipe A fills a tank at the rate of 100lit/min, Pipe B fills at the rate of 25 lit/min, pipe C drains at the rate of 50 lit/min. The three pipes are kept open for one minute each, one after the other. If the capacity of the tank is 7000 liters, how long will it take to fill the tank if
(i) A is kept open first, followed by B and then C.
(ii) B first, followed by A, and then C.
(iii) B first, followed by C, and then A.
(A)279.25 mins, 280 mins and 280 mins
(B) 280 mins, 280 mins and 279.25 mins
(C) 279 mins, 280 mins and 279.25 mins
(D) 277 mins, 277 mins 45 sec and 280 mins
Answer: D
Explanation:
(i) A is kept open first, followed by B and then C
Each cycle of 3 minutes, 75 liters get filled. 100 + 25 - 50. So, after 3 minutes the tank
would have 75 liters
6 mins - 150 liters
9 mins - 225 liters
30 mins - 750 liters
270 mins - 6750 liters
273 mins - 6825 liters
276 mins - 6900 liters
Now, A will be open, A can fill 100 liters in a minute.
277 mins - 7000 liters
So, it would take 277 mins to fill the tank.
The most important thing in these type of questions is to think in terms of cycles till we reach close to the required target and then think in simple steps.
(ii) B first, followed by A, and then C
Each cycle of 3 minutes, 75 liters get filled. 25 + 100 - 50. So, after 3 minutes the tank
would have 75 liters.
6 mins - 150 liters
9 mins - 225 liters
30 mins - 750 liters
270 mins - 6750 liters
273 mins - 6825 liters
276 mins - 6900 liters
Now, B will be open, B can fill 25 liters in a minute.
277 mins - 6925 liters
Now, A will be open, A can fill 100 liters in a minute. Therefore, A can fill 75 liters in 45 seconds.
277 mins 45 sec - 7000 liters
So, it would take 277 mins 45 sec .
(iii) B first, followed by C, and then A
In this case also, Each cycle of 3 minutes, 75 liters get filled. 25 -50 + 100. But there is a small catch here. In the first set of 3 minutes, we would fill up to about 100 liters. After 1 minute, we would be at 25 liters, after 2 minutes, we would be at 0 liters and in the third minute, the tank would be 100 liters full.
6 mins - 175 liters
9 mins - 250 liters
30 mins - 775 liters
270 mins - 6775 liters
273 mins - 6850 liters
276 mins - 6925 liters
Now, B will be open, B can fill 25 liters in a minute.
277 mins - 6925 liters
Now, C will be open, C will drain 50 liters in a minute.
278 mins - 6875 liters
Now, A will be open, A can fill 100 liters in a minute.
279 mins - 6975 liters
Now, B will be open, B can fill 25 liters in a minute.
280 mins - 7000 liters
So, it would take 280 mins to fill the tank.
The most important thing in these type of questions is to think in terms of cycles till we reach close to the required target and then think in simple steps.
The question is "how long will it take to fill the tank if"
Hence, the answer is "277 mins, 277 mins 45 sec and 280 mins".
Question 4: 4 men and 6 women complete a task in 24 days. If the women are at least half as efficient as the men, but not more efficient than the men, what is the range of the number of days for 6 women and 2 men to complete the same task?
(A) 30 to 33.6 days
(B) 32 to 35 days
(C) 33.6 to 35 days
(D) 30 to 35 days
Answer: A
Explanation:
4m and 6w finish in 24 days.
In one day, 4m + 6w = 1/24 of task.
In these questions, just substitute extreme values to get the whole range
If a woman is half as efficient as man
4m + 3m = 1/24, 7m = 1/24, m = 1/168
6w + 2m = 3m + 2m = 5m, 5m will take 168/5 days = 33.6 days
If a woman is as efficient as a man
4m + 6w finish in 24 days
10m finish 1/24 of task in a day
6w + 2m = 8m, 8m will take 240/8 = 30 days to finish the task.
So, the range = 30 to 33.6 days. The new team will take 30 to 33.6 days to finish the task.
The question is "what is the range of the number of days for 6 women and 2 men to complete the same task?"
Hence, the answer is "30 to 33.6 days".
Question 5: A fill pipe can fill a tank in 20 hours, a drain pipe can drain a tank in 30 hours. If a system of n pipes (fill pipes and drain pipes put together) can fill the tank in exactly 5 hours, which of the following are possible values of n (More than one option could be correct)?
1. 32
2. 54
3. 29
4. 40
(A) 1 and 2 only
(B) 1 and 3 only
(C) 2 and 4 only
(D) 2 and 3 only
Answer: D
Explanation:
3 fill pipes cancel out 2 drain pipes. Plus, you need an additional 4 fill pipes fill the tank in
5 hours. so the answer has to be 5k + 4.
Both 54 and 29 are possible.
The question is "which of the following are possible values of n?"
Hence, the answer is "2 and 3 only".
Question 6: Consider three friends A, B and C who work at differing speeds. When the slowest two work together they take n days to finish a task. When the quickest two work together they take m days to finish a task. One of them, if he worked alone would take thrice as much time as it would take when all three work together. How much time would it take if all three worked together?
(A)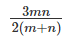
(B) 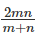
(C) 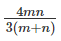
(D) 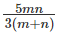
Answer: C
Explanation:
Let A < B < C in terms of efficiency.
B and C together take n days.
A and B together take m days.
One of them, if he worked alone would take thrice as much time as it would take when all three work together. This is a crucial statement. Now, if there are three people who are all equally efficient, for each of them it would take thrice as much time as for all three together.
Now, this tells us that the person who takes thrice as much time cannot be the quickest one. If the quickest one is only one-third as efficient as the entire team, the other two cannot add up to two-thirds. By a similar logic, the slowest one cannot be the person who is one-third as efficient.
In other words, the person one-third as efficient = B
Let A, B and C together take x days. B alone would take 3x days
B and C together take n days. Or B + C in 1 day do
1/n of the task ........Eqn (i)
A and B together take m days. Or, A + B in 1 day do
1/m of the task ........Eqn (ii)
B takes 3x days to do the task. Or, B, in one day, does
1/3x of the task ........Eqn (iii)
Now, if we do (i) + (i) – (iii) we get
A + B + C do 1/n + 1/m - 1/3x in a day. This should be equal to 1/x as all three of them complete the task in x days.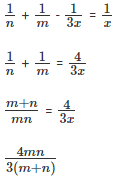
The question is "How much time would it take if all three worked together?"
Hence, the answer is " 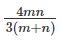 "
"
Question 7: Pipes A, B and C can fill a tank in 30, 60 and 120 minutes respectively. Pipes B and C are kept open for 10 minutes, and then Pipe B is shut while Pipe A is opened. Pipe C is closed 10 minutes before the tank overflows. How long does it take to fill the tank?
(A) 40 minutes
(B) 28 minutes
(C) 30 minutes
(D) 36 minutes
Answer: C
Explanation:
Let us assume that the tank has a capacity of 120 litres. So, the pipes discharge the following amounts of water:
(A) 4 litres per minute
(B) 2 litres per minute
(C) 1 litre per minute.
Part 1: B and C (3 litres/min) are kept open for 10 minutes, filling 3 × 10 = 30 litres. 90 litres remain to be filled in the tank.
Part 2: Now, B is shut and A is opened. Effectively, this means that A and C are filling the tank together (5 litres / minute). We don’t yet know how long A and C are open together.
Part 3: C is closed 10 minutes before the tank overflows. This means that only A works for the last 10 minutes, filling 40 litres (working@4 litres/min)
Since 30 litres are filled in Part 1 and 40 litres in Part 3, the balance (50 litres) should have been filled in Part 2.
Working together, A and C fill 5 litres per minute in Part 2. This means that they would have taken 10 minutes to fill 50 litres.
So, the entire time it took to fill the tank is:
10 + 10 + 10 = 30 mins.
Alternate Solution
In one minute, A fills (1/30)th of the tank, B fills (1/60)th of the tank, and C fills (1/120)th of the tank.
(B + C) work for 10 minutes, followed by (A + C), which works for “t” minutes, followed by A, which work for 10 minutes. This ensures that the tank gets filled. This can be written in an equation form:
10 * (1/60 + 1/120) + t * (1/30 + 1/120) + 10 * (1/30) = 1
10 * (1/40) + t * (1/24) + 10 * (1/30) = 1.
Or, 1/4 + t/24 + 1/3 = 1. Or t = 10.
So, the entire tank was filled in 30 mins.
The question is "How long does it take to fill the tank?"
Hence, the answer is "30 minutes".
Question 8: B takes 12 more days than A to finish a task. B and A start this task and A leaves the task 12 days before the task is finished. B completes 60% of the overall task. How long would B have taken to finish the task if he had worked independently?
(A) 48 days
(B) 36 days
(C) 28 days
(D) 32 days
Answer: B
Explanation:
Let us say A and B split their share of the task and started doing their respective shares simultaneously.
Let’s say A takes A days to finish the task. Therefore, B takes A + 12 days to finish the entire task.
A has to finish 40% of the task, since B is doing the rest. So A will only take 2A/5 number of days.
B only has to finish 60% of the task, so B will take (3(A+12)/5) number of days.
But as we know, B starts working along with A and finishes 12 days after A stops working.
So, (3(A+12)/5) = ((2A)/5+12)
3A + 36 = 2A + 60
A = 24; B = 36 days.
The question is "How long would B have taken to finish the task if he had worked independently?"
Hence, the answer is "36 days".
Question 9: A and B together can finish a task in 12 days. If A worked half as efficiently as he usually does and B works thrice as efficiently as he usually does, the task gets completed in 9 days. How long would A take to finish the task if he worked independently?
(A) 12 days
(B) 24 days
(C) 27 days
(D) 18 days
Answer: D
Explanation:
Let A take ‘a’ days to complete the task and B take ‘b’ days to complete the task.
Thus in one day, A will complete (1/a)th of the task.
Similarly in one day, B will complete (1/b)th of the task.
So in one day, if A and B work together they will complete (1/a + 1/b)th of the task.
Given that A and B together take 12 days to complete the task, then in one day A and B together complete (1/12)th of the task.
Thus, 1/a + 1/b = 1/12 ……Eqn. 1
If A worked half as efficiently as he usually does, then A will take twice the time as he usually takes, i.e., 2a days. Thus in one day, A completes (1/2a)th of the task.
Similarly if B worked thrice as efficiently as he usually does, then B will take one-third the time he usually takes, i.e., b/3 days. Thus in one day, B completed (1/(b⁄3))th or (3/b)th of the task.
Thus when both of them work together, they will complete (1/2a + 3/b)th of the task, given that A and B take 9 days to complete the task.
Thus, 1/a + 1/b = 1/12 ……Eqn. 1
1/2a + 3/b = 1/9 …… Eqn. 2
1/2a + 3/b = 1/9 …… Eqn. 2
Solving Equations 1 and 2 for ‘a’ we should get the answer,
From equation (1) we get 12(a + b) = ab
From equation (2), we get 9(b + 6a) = 2ab
Substituting ab as 12(a + b) in equation (2) we get 9b + 54a = 2 x 12 x ( a + b)
9b + 54a = 24a + 24b;
Or, 30a = 15b,
Or, b = 2a
Now, 12(a + b) = ab, or 12 x 3a = 2a2
a = 18 days.
The question is "How long would A take to finish the task if he worked independently?"
Hence, the answer is "18 days".
Question 10: B takes 12 more hours than A to complete a task. If they work together, they take 16 fewer hours than B would take to complete the task. How long will it take A and B together to complete a task twice as difficult as the first one?
(A) 16 hrs
(B) 12 hrs
(C) 14 hrs
(D) 18 hrs
Answer: A
Explanation:
Let us assume that A takes ‘x’ hours to finish a task. Then, B takes ‘x+12’ hours to finish the same task. Given, if they work together, they take 16 fewer hours than B would take to
complete the task = ‘x-4’ hours.
A completes the task in ‘x’ hours => A finishes 1/x th of the task in 1 hour.
B finishes the 1/(x+12)th of the task in 1 hour.
A and B finish 1/(x−4)th of the task in one hour .
Therefore, 1/x + 1/(x+12) = 1/(x−4).
Solving for x, we get 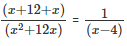
(2x+12)(x-4) = x2 + 12x.
x2 – 8x -48 =0.
x2 – 12x + 4x - 48 = 0
x (x - 12) + 4 (x - 12)
(x - 12) (x + 4) = 0. X=12 or x=-4. Only x =12 is possible, since x cannot be negative.
Therefore, when A and B work together they finish a task in x - 4 = 12 - 4 = 8 hours.
If the task is twice as difficult as the first one, they finish it in 2 * 8 = 16 hours.
The question is "How long will it take A and B together to complete a task twice as difficult as the first one?"
Hence, the answer is "16 hrs".
|
167 videos|238 docs|95 tests
|
FAQs on Question with Answers: Pipes and Cistern - 1 - Quantitative Aptitude (Quant) - CAT
| 1. What is a pipe and cistern problem in mathematics? |  |
| 2. How can I solve pipe and cistern problems? |  |
| 3. What is the formula to calculate the time taken to fill a cistern using multiple pipes? |  |
| 4. How do you find the filling rate of a pipe in a pipe and cistern problem? |  |
| 5. Can you provide an example of a pipe and cistern problem? |  |
















