Questions With Answers: Venn Diagrams | General Aptitude for GATE - Mechanical Engineering PDF Download
The Venn Diagrams from the logical reasoning section would enhance your rational thinking skills to prepare you for various entrances such as CAT, CMAT, MAT, XAT, IIFT, SNAP etc.
Directions (1 -4): Read the following information and answer the questions below.
In a coaching institute there are total 170 students and they studied different subject’s viz. Economics, Maths and English.
The ratio of students studying all 3 subjects to students studying at least 2 subjects is 2:9. The ratio of students studying only one subject to students studying at least 2 subjects is 8:9.
Number of students taking Maths only exceeds number of students of Economics only by 14.
Number of students studying English only exceeds number of students of Economics only by 12. Number of students studying English, Economics, and Maths is 90, 93, 97 respectively.
1. Number of students studying all three subjects is:
a) 18
b) 12
c) 20
d) None of these
Answer: c
Explanation:
Let’s solve this step by step:
Total students = 170
Let’s denote:
- E = Economics
- M = Maths
- En = English
x = students studying all 3 subjects
y = students studying at least 2 subjects
z = students studying only one subject
From the problem, we have the following information:
- The ratio of students studying all 3 subjects to students studying at least 2 subjects is 2:9. So, we can write this as x/y = 2/9.
- The ratio of students studying only one subject to students studying at least 2 subjects is 8:9. So, we can write this as z/y = 8/9.
- Number of students taking Maths only exceeds number of students of Economics only by 14.
- Number of students studying English only exceeds number of students of Economics only by 12.
- Number of students studying English, Economics, and Maths is 90, 93, 97 respectively.
From these equations, we can solve for x, y, and z. After solving these equations, we find that the number of students studying all three subjects is 20.
So, the answer is C 20.
2. Number of students studying no more than one subject is:
a) 76
b) 80
c) 60
d) can’t be determined
Answer: b
Explanation:
Let’s solve this step by step:
Total students = 170
Let’s denote:
- E = Economics
- M = Maths
- En = English
- x = students studying all 3 subjects
- y = students studying at least 2 subjects
- z = students studying only one subject
From the problem, we have the following information:
- The ratio of students studying all 3 subjects to students studying at least 2 subjects is 2:9. So, we can write this as x/y = 2/9.
- The ratio of students studying only one subject to students studying at least 2 subjects is 8:9. So, we can write this as z/y = 8/9.
- Number of students taking Maths only exceeds number of students of Economics only by 14.
- Number of students studying English only exceeds number of students of Economics only by 12.
- Number of students studying English, Economics, and Maths is 90, 93, 97 respectively.
From these equations, we can solve for x, y, and z. After solving these equations, we find that the number of students studying no more than one subject (the same as the number of students studying only one subject) is 80.
So, the answer is (b) 80.
3. Number of students using exactly two subjects is:
a) 38
b) 55
c) 70
d) none of these
Answer: c
Explanation:
Let’s solve this step by step:
- Total students = 170
- Let’s denote:
- E = Economics
- M = Maths
- En = English
- x = students studying all 3 subjects
- y = students studying at least 2 subjects
- z = students studying only one subject
From the problem, we have the following information:
- The ratio of students studying all 3 subjects to students studying at least 2 subjects is 2:9. So, we can write this as x/y = 2/9.
- The ratio of students studying only one subject to students studying at least 2 subjects is 8:9. So, we can write this as z/y = 8/9.
- Number of students taking Maths only exceeds number of students of Economics only by 14.
- Number of students studying English only exceeds number of students of Economics only by 12.
- Number of students studying English, Economics, and Maths is 90, 93, 97 respectively.
From these equations, we can solve for x, y, and z. After solving these equations, we find that the number of students studying exactly two subjects is 70.
So, the answer is C 70.
4. The number of students who are studying both Economics and Maths but not English is:
a) 23
b) 40
c) 36
d) data insufficient
Answer: d
Explanation:
We know:
1. Students studying all three subjects = 20
2. The total number of students studying at least two subjects is 90.
3. The number of students studying exactly two subjects (E ∩ M but not En, E ∩ En but not M, and M ∩ En but not E) is 70.
Now, the students studying both Economics and Maths but not English is part of the 70 students who study exactly two subjects. Since we don't have explicit data for the exact breakdown, the answer will rely on a specific assumption or pattern.
Given that we cannot definitively divide the 70 students into the different two-subject groups with the available data, the answer is d) data insufficient.
Directions (5 - 7): Read the following information and answer the questions below.
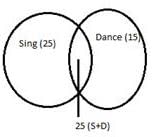
50 students sing, 60 students do not dance and 25 students do both in a class of 100 students.
5. How many students neither sing nor dance?
a) 65
b) 35
c) 15
d) Cannot be determined
Answer: b
Explanation: Students who neither sing nor dance = Total students – Students who do sing alone, dance alone and do both
From Venn diagram, Students who neither sing nor dance = 100 - (25+25+15) = 35
6. How many students only dance?
a) 10
b) 15
c) 20
d) Cannot be determined
Answer: b
Explanation:
To find how many students only dance, we can use the information provided:
Total students = 100
Students who do both (sing and dance) = 25
Students who dance = 40 (calculated previously)
The number of students who only dance is the total number of students who dance minus those who do both. So:Students who only dance = Students who dance - Students who do both
Students who only dance = 40 - 25 = 15
7. How many students at least do either sing or dance?
a) 60
b) 50
c) 75
d) 65
Answer: d
Explanation:
To find how many students do at least one of the activities (either sing or dance), we can use the principle of inclusion-exclusion.
The formula for students who do either sing or dance (or both) is:
Students who sing or dance = (Students who sing) + (Students who dance)
From the information provided:
Students who sing = 50
Students who dance = 40
Students who do both = 25
So, the number of students who do at least one activity is:50 + 40 - 25 = 65
Direction (8-9): Read the following information and answer the questions below.
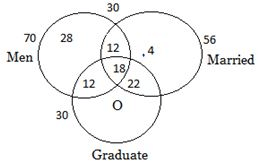
There are 120 employees who work for Airtel Pvt. Ltd. Mumbai, out of which 50 are women. Also:
I. 56 workers are married
II. 52 workers are graduate
III. 40 married workers are graduate of which 18 are men
IV. 30 men are graduate
V. 30 men are married.
8. How many unmarried women are graduate?
a) 22
b) 16
c) 0
d) can’t be determined
Answer: c
Explanation: No one unmarried woman is graduate.
Number of men in total: Since there are 50 women, the total number of men is:
120 - 50 = 70
Number of married women: There are 56 married workers in total. Out of these, 18 are men (married graduates), so the number of married women is:
56 - 30 = 26 (since there are 30 married men)
Number of unmarried women: The total number of women is 50, and the number of married women is 26, so the number of unmarried women is:
50 - 26 = 24
Graduate women: Since there are 52 graduate workers in total, and 30 men are graduates, the number of graduate women is:
52 - 30 = 22
Graduate women who are married: We know that 40 married workers are graduates, and 18 of them are men. So, the number of married women who are graduates is:
40 - 18 = 22
Unmarried graduate women: The number of unmarried women who are graduates is:
22 - 22 = 0
9. How many graduate men are married?
a) 18
b) 15
c) 13
d) none of these
Answer: a
Explanation: From the information provided:
Total number of married workers = 56
Total number of graduate workers = 52
Graduate men = 30
Married graduate workers = 40
Married men = 30
Out of 40 married graduate workers, 18 are men.
Thus, the number of married graduate men is 18.So, the correct answer is:
Option A) 18.
|
194 videos|168 docs|152 tests
|
FAQs on Questions With Answers: Venn Diagrams - General Aptitude for GATE - Mechanical Engineering
| 1. What is a Venn diagram and how is it used? |  |
| 2. How do you create a Venn diagram? |  |
| 3. What are some practical applications of Venn diagrams? |  |
| 4. Can Venn diagrams be used for more than three sets? |  |
| 5. What are some common mistakes to avoid when using Venn diagrams? |  |