Introduction to Complex Number | Mathematics (Maths) for JEE Main & Advanced PDF Download

Definition of  Complex Number 

Complex Numbers are the numbers which along with the real part also have the imaginary part included with it.
It is defined as the combination of real part and imaginary part. Either of the parts can be zero.
If ‘a’ is the real part and ‘b’ represents the imaginary part, then the complex number is represented as 
 z = a + ib where i, stands for iota which itself is a square root of negative unity.

Examples:

Complex Number	Real Part	Imaginary Part
3 + 5i	3	-5
5	5	0
-2i	0	-2

Thus, we can also write z = Re(z) + i Im(z). This form of representation is also called as the Cartesian or algebraic form of representation.

If z = -2 + j4, then Re(z) = -2 and Im(z) = 4.

Similarly, for z = 3+j5, Re(z) = 3 and Im(z) = (5).

Representation of Complex Number 

Complex Number have many ways in which it can be expressed. Some of the most commonly used forms are:

• Cartesian or algebraic or rectangular form

• Trigonometric or polar form

• Exponential form

• Vector form

Can we take the square-root of a negative number?

Yes of course, but to understand this question, let’s go into more deep of complex numbers,

Consider the equation x2+1 = 0, If we try to get its solution, we would stuck at x = √(-1) so in Complex Number we assume that √(-1) =i or i2 =-1

which means i can be assumed as the solution of this equation. i is called as Iota in Complex Numbers.

We can further formulate as,

i2 = -1

i3 = i2 * i = -i

i4 =i2 * i2 =1

So, we can say now, i4n = 1 where n is any positive interger.

Also, note that i + i2 + i3 + i4 = 0 or in + i2n + i3n + i4n= 0

This means sum of consecutive four powers of iota leads the result to zero.

What is the form a + ib?

We know from the above discussion that, Complex Numbers can be represented in four different ways. Out of which, algebraic or rectangular form is one of the form.
Z = a + ib is the algebraic form in which ‘a’ represents real part and ‘b’ represents imaginary part. Two mutually perpendicular axes are used to locate any complex point on the plane. Horizontal axis represents real part while the vertical axis represents imaginary part.

 

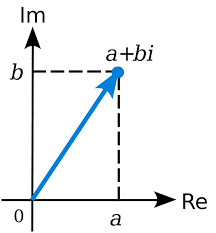
How do we locate any Complex Number on the plane?  
Let us take few examples to understand that, how can we locate any point on complex or argand plane?

Example 1:
Consider a complex number z = 6 +j4 (‘i’ and ‘j’, both can be used for representing imaginary part), if we compare this number with z = a + jb form. Then we can easily equate the two and get a = 6 and b = 4. Since both a and b are positive, which means number will be lying in the first quadrant. ‘z’ will be 6 units in the right and 4 units upwards from the origin. You can see the same point in the figure below.

Example 2:
Now consider a point in the second quadrant that is. z = -7 + j6, Here since a= -7 and b = 6 and thus will be lying in the second quadrant.
Point z is 7 units in the left and 6 units upwards from the origin. Refer the figure to understand it pictorially.

Example 3:
Now let’s consider a point in the third quadrant as z = -2 – j3. Since in third quadrant both a and b are negative and thus a = -2 and b = -3 in our example. This point will be lying 2 units in the left and 3 units downwards from the origin.

Example 4:
Let now take the fourth (of fourth quadrant) and the last case where z = 5 – j6. Here, a = 5 and b = - 6 i.e. a positive and b negative. This point will be lying 5 units in the right and 6 units downwards.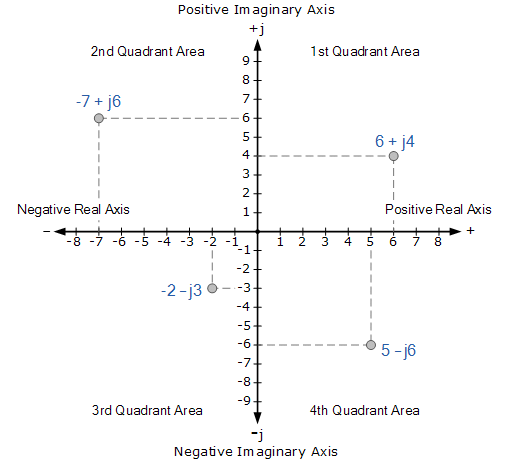



Are all Real Numbers  Complex Numbers?

Complex number has two parts, real part and the imaginary part.

that is. z = a + ib

if b = 0, z = a which is called as the Purely Real Number

and if a = 0, z = ib which is called as the Purely Imaginary Number.

Thus we can say that all real numbers are also complex number with imaginary part zero.

What is the application of Complex Numbers?
Complex Numbers have wide variety of applications in a variety of scientific and related areas such as electromagnetism, fluid dynamics, quantum mechanics, vibration analysis, cartography and control theory.

Complex Equations 

Any equation involving complex numbers in it are called as the complex equation.

For example: x = (2+3i) (3+4i), In this example, x is a multiple of two complex numbers. On multiplying these two complex number we can get the value of x.

z2 + 2z + 3 = 0 is also an example of complex equation whose solution can be any complex number.

Solved Examples

Illustration 1: Let a and b be roots of the equation x2 + x + 1 = 0. Then find the equation whose roots are a = 19 and b = 7.
Solution: Given that x2 + x + 1 = 0.
This means that either x = ω or x = ω2.
Hence, a19 = ω19 and b7 = ω14 = ω2
Hence, the equation becomes x2 – (ω + ω2)x + ω ω2 = 0.
Hence the required equation is x2 + x + 1 = 0.

Illustration 2: Dividing f(z) by z - i, we obtain the remainder i and dividing it by z + i, we get remainder 1 + i. Find the remainder upon the division of f(z) by z2 + 1.
Solution: z – i = 0 gives z = i.
Remainder when f(z) is divided by (z – i) = f(i).
Similarly, the remainder when f(z) is divided by (z + i) = f(- i)   ….. (1)
According to question f(i) = i
and f( -i) = 1 + i.     ..... (2)
Since, z2 + 1 is a quadratic expression, therefore remainder when f(z) is divided by z2 + 1 will be in general a linear expression.
Let g(z) be the quotient and az + b the remainder when g(z) is divided by z2 + 1.
Then f(z) = g(z) (z2 + 1) + az + b              ..... (3)
So, f(i) = g(i) (i2 + 1) + ai + b = ai + b        .… (4)
and f(-i) = g(-i) (i2 + 1) – ai + b = -ai + b    .… (5)
From (1) and (4), we have b + ai = i              .… (6)
from (2) and (5) we have b – ai = 1 + i           …. (7)
Solving (6) and (7), we have b = ½ + i and a = i/2.
Hence, the required remainder  = az + b = ½ iz + ½ + i.

Illustration 3: Find all complex numbers z for which arg [(3z-6-3i)/(2z-8-6i)] = π/4 and |z-3+4i| = 3.
Solution: We have

= = Since arg(a + ib) = π/4, so tan π/4 = b/a which gives a = b

So, 6x2 + 6y2 – 36x – 24y + 66 = 12x – 12y -12

So, x2 + y2 – 8x – 2y + 13 = 0 . … … (1)

Again, |z – 3 + i| = 3 gives |x + iy - 3 + i| = 3

So, (x-3)2 + (y+1)2 = 9

This yields x2 + y2 - 6x + 2y +1 = 0 …. (2)

Subtracting (2) form (1), we have

-2x – 4y + 12 = 0

This gives x = – 2y + 6 … (3)

Putting the value of x in (2), we get

(-2y + 6)2 + y2 – 6 (-2y + 6) + 2y + 1 = 0

So, 5y2 – 10 y +1 = 0

So, y = (-10 ± 4√5) /10

= 1 ± 2/√5

So, x = – 2y + 6 = 4 ∓ (- 4)/√5

so, z = x + iy = 4 ∓ 4/√5 + i (1 ± 2/√5)