Linear Inequalities in One Variable and Two Variables | Mathematics (Maths) for JEE Main & Advanced PDF Download
Understanding Linear Inequation
Example 1
Let’s say that your mother sends you to a shop to buy rice. She gives you Rs 200 and instructs you to buy the maximum quantity possible. In the shop, rice is available at Rs 30 per kg and in packets of 1 kg each. Let’s convert this statement into an expression:
If ‘x’ is the number of packets purchased by you, then the total amount spent will be 30x (since one packet of rice weighing 1 kg costs Rs 30). Now, you have to buy the maximum amount of rice within Rs 200. Since 200 is not divisible by 30, you will not be able to spend the entire amount. Hence, the expression will be:
30x < 200 … (1)
Note, that this expression does not have an equal sign and hence is not an equation. It is an inequality.
Example 2
You go to a shop to buy some chocolates and biscuits. You want to spend up to Rs 120. One chocolate costs Rs 40 and one packet of biscuits costs Rs 20. Let’s convert this to an expression too:
If ‘x’ is the number of chocolates and ‘y’ is the number of biscuits purchased by you, then the total amount spent is (40x + 20y). Notice that 120 is divisible by 60 (40+20). Also, the statement says that you want to spend ‘up to Rs 120’. Hence,
40x +20y ≤ 120 … (2)
Observe that this expression has two parts,
• 40x + 20y < 120 … (3) … not an equation. It is an inequality.
• 40x + 20y = 120 … (4) … an equation.
Definition 1
Two real numbers or two algebraic expressions related by the symbol ‘<’, ‘>’, ‘≤’ or ‘≥’ form an inequality. Here are some examples of inequalities:
• Numerical inequalities: 3 < 5; 7 > 5.
• Literal inequalities or inequalities which involves variables: x>=2; y <=5.
• Double inequalities: 3 < 5 < 7; 5 < x < 9.
• Strict inequalities or inequalities that have either ‘<’ or ‘>’ in the equation: ax + b < 0; ax + b > 0; ax + by < c; ax + by > c.
• Slack inequalities or inequalities that have a ‘≤’ or ‘≥’ sign: ax + b ≤ 0; ax + b ≥ 0; ax + by ≤ c; ax + by ≥ c.
• Linear inequalities in one variable – ‘x’ where a ≠0: ax + b >0; ax + b ≤ 0.
• Linear inequalities in two variables – ‘x’ and ‘y’ where a ≠ 0 and b ≠ 0: ax + by < c; ax + by ≥ c.
Remark: ax2 + bx + c < 0 is an example of a quadratic inequality in ‘x’ where a ≠ 0.
Linear Inequations in One Variable – Algebraic Solutions and Graphical Representation
Let’s look at example 1 from above. From equation (1), we have
30x < 200
Now, since x is the number of packets purchased, it cannot be a fraction or a negative integer. In this inequality, LHS = 30x and RHS = 200. Therefore, let’s calculate the value of LHS for different values of ‘x’ and try to find the solution to the inequality. We have,
• For x = 0, L.H.S. = 30 (0) = 0. ∴ LHS < RHS (0 < 200) is true.
• For x = 1, L.H.S. = 30 (1) = 30 ∴ LHS < RHS (30 < 200) is true.
• For x = 2, L.H.S. = 30 (2) = 60 ∴ LHS < RHS (60 < 200) is true.
• For x = 3, L.H.S. = 30 (3) = 90 ∴ LHS < RHS (90 < 200) is true.
• For x = 4, L.H.S. = 30 (4) = 120 ∴ LHS < RHS (120 < 200) is true.
• For x = 5, L.H.S. = 30 (5) = 150 ∴ LHS < RHS (150 < 200) is true.
• For x = 6, L.H.S. = 30 (6) = 180 ∴ LHS < RHS (180 < 200) is true.
• For x = 7, L.H.S. = 30 (7) = 210 ∴ LHS < RHS (210 < 200) is false.
Therefore, we find that the inequality is true for x = 0, 1, 2, 3, 4, 5, and 6. These values are called solutions of the inequality and the set {0, 1, 2, 3, 4, 5, 6} is called the solution set. Hence, we have:
Any solution of an inequality in one variable is a value of the variable which makes it a true statement.
While solving linear equations, we followed the following rules:
• Rule 1: Equal numbers may be added to (or subtracted from) both sides of an equation.
• Rule 2: Both sides of an equation may be multiplied (or divided) by the same non-zero number.
For solving an inequality, we follow similar rules with slight modifications as given below
Rule 1: Equal numbers may be added to (or subtracted from) both sides of an inequality without affecting the sign of inequality.
Rule 2: Both sides of an inequality can be multiplied (or divided) by the same positive number. But when both sides are multiplied or divided by a negative number, then the sign of inequality is reversed. For example, 3 > 2 while – 3 < – 2. Also, – 8 < – 7, whereas (– 8)( – 2) > (– 7)( – 2) i.e. 16 > 14.
To understand the application of the rules, let’s solve 30x < 200 in two scenarios:
1. ‘x’ is a natural number
2. ‘x’ is an integer. 3(x – 1) ≤ 2 (x – 3)
We are given, 30 x < 200. By Rule 2, we know that we can divide both sides of an inequality by the same positive number. Hence, 30x/30 < 200/30. Or, x < 20/3
• If ‘x’ is a natural number, then the solution set of the inequality is {0, 1, 2, 3, 4, 5, 6}
• If ‘x’ is an integer, then the solution set is {…, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6}
Graphical Representation of the Solution of Linear Inequations
Example: Solve 7x + 3 < 5x + 9. Show the graph of the solutions on the number line.
Solution: We have, 7x + 3 < 5x + 9
Using Rule 1, we have,
7x – 5x < 9 – 3
⇒ 2x < 6
⇒ x < 3
This can be represented graphically, as follows:

More Solved Examples for You
Q1. Solve x/3 > x/2 + 1 where x is a real number.
Answer. We have,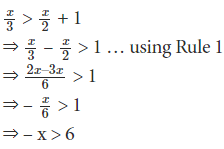
Or, x < – 6 … using Rule 2.
Therefore, the solution set of the inequality consists of all real numbers less than (- 6) and is denoted as {….., -8, -7, -6}.
Graphical Solution for Solving Inequalities in Two Variables
We know that a line divides a Cartesian two-dimensional plane is into two parts called half-planes.
• A vertical line divides it into left and right half planes as shown below:
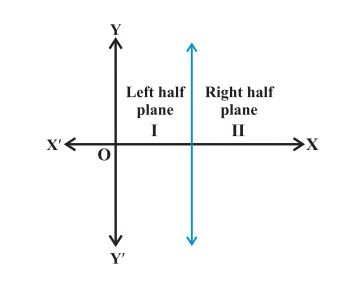
• A non-vertical line divides the plane into lower and upper half-planes as shown below:
linear inequalities in two variables
1/(|x| – 3) ≤ ½
Any point in the Cartesian plane will either:
• lie in the line or
• lie in half-plane I or
• lie in half-plane II
Let’s look at the relationship between the points in the plane and the inequalities ax + by < c or ax + by > c. An expression in two variables, ‘x’ and ‘y’ and a constant ‘c’, can have three possibilities:
1. ax + by = c
2. ax + by > c
3. ax + by < c
where a ≠ 0 and b ≠ 0. Let’s look at each scenario:
1. ax + by = c
In this case, all points having coordinates (x, y) satisfying the equation ax + by = c lie on the line representing it. Conversely, all points which lie on the line represented by ax + by = c satisfy the equation.
2. ax + by > c
In this case, we will look at two further scenarios:
i. b > 0
ii. b < 0
Let’s look at the first scenario where b > 0. As shown in the figure below, consider a point P(α, β) on the line ax + by = c, where b > 0.
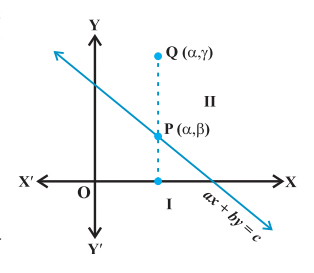
Since the point P lies on the line, we have aα + bβ = c. Next, take a point Q(α, γ) in the half-plane II as shown above. Since the point Q lies above the point P, we have
γ > β
Multiplying both sides by ‘b’, we get
bγ > bβ
Adding ‘aα’ to both sides, we have
aα + bγ > aα + bβ
∴ aα + bγ > c … (since aα + bβ = c)
Hence, we can say that the point Q(α, γ) satisfies the inequality aα + bγ > c. We can also state that all points lying in half-plane II (b > 0), above the line ax + by = c, satisfy the inequality ax + by > c.
Converse
Let the point P(α, β) be a point on the line ax + by = c and the point Q(α, γ) satisfying the inequality ax + by > c. Therefore, we have
aα + bγ > c
⇒ aα + bγ > aα + bβ … (since P(α, β) satisfies ax + by = c, we have aα + bβ = c)
⇒ bγ > bβ
⇒ γ > β … thereby indicating that the point Q(α, γ) lies in the half-plane II.
To sum it up: Any point in the half plane II satisfies ax + by > c, and conversely, any point satisfying the inequality ax + by > c lies in half plane II. Similarly, for b < 0, it can be proved that any point satisfying the inequality ax + by > c lies in the half-plane I and conversely.
Here are some pointers to graphically represent and solving inequalities in two variables:
• Solution region is the region containing all solutions of the inequality.
• To identify the half-plane represented by the inequality, you can take a point (a, b) which does not lie on the line and check if it satisfies the inequality. If it does, then the inequality represents the half-plane containing the point and you can shade the region. If it doesn’t then the half-plane that does not contain the point should be shaded. For convenience, you can take the point (0, 0) to check if it satisfies the inequality.
• If the inequality is of the type ax + by ≥ c or ax + by ≤ c, then include the points on the line ax + by = c in the solution region. To do so, draw a dark line on the line representing ax + by = c.
• If the inequality is of the type ax + by > c or ax + by < c, then don’t includes the points on the line ax + by = c in the solution region. Draw a broken/dotted line in this case.
Example 1
Question: Let’s solve the following inequality 40x + 20y ≤ 120 … (1), where x and y are whole numbers (not fractions or negative numbers).
Solution: To solve this, let’s start with substituting x = 0 in the LHS of the inequality (1).
Therefore, we get
40x + 20y = 0 + 20y = 20y
Hence, we have
20y ≤ 120
⇒ y ≤ 6
So, for x = 0, the values of y can be 0, 1, 2, 3, 4, 5, and 6. The solutions can be written as
(0, 0), (0, 1), (0,2), (0,3), (0,4), (0, 5) and (0, 6). Similarly,
For x = 1, the solutions are (1, 0), (1, 1), (1, 2), (1, 3), (1, 4)
For x = 2, the solutions are (2, 0), (2, 1), (2, 2)
For x = 3, the solution is (3, 0)
For x = 4, the value of y becomes negative and hence not valid.
These solutions can be represented as follows:
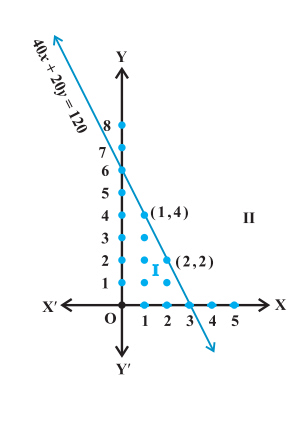
Let’s try to extend this solution to real numbers. For this, draw a graph for the equation 40x + 20y = 120. Now, let’s consider a point (0, 0) and check if it satisfies the inequality.We have,
40x + 20y ≤ 0
Substituting the values of ‘x’ and ‘y’, we get
40(0) + 20(0) ≤ 0
Or, 0 ≤ 0 which is true. Hence, we can conclude that the point (0, 0) satisfies the inequality. Look at the diagram given below: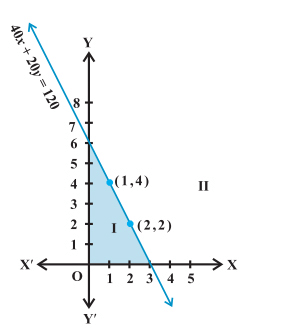
In the diagram, you can see that the point (0, 0) lies in the half-plane I. Hence, the inequality represents this plane. Also, the points on the line satisfy the inequality. Hence, it is also a part of the shaded region.
Solving Inequalities:
A question on solving inequalities in two variables
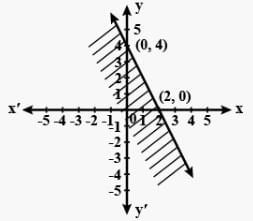
Question: Solve 3x + 2y > 6 graphically in a two-dimensional plane.
Solution: To solve the inequality, let’s plot a graph of the equation 3x + 2y = 6 as shown below:
This line divides the plane into half-planes I and II. Next, we select a point (0, 0) and determine if it satisfies the given inequality. Hence, we have
3x + 2y > 6
⇒ 3(0) + 2(0) > 6
⇒ 0 > 6 which is FALSE.
Since (0, 0) lies in the half-plane I and it does not satisfy the inequality, half-plane I, is not the solution. Also, the inequality given is a ‘Strict inequality’. Hence, any point on the line represented by 3x + 2y = 0 does not satisfy the inequality either. Therefore, the solution of the inequality is the shaded region in the diagram above.
A question on a system of linear inequalities in two variables
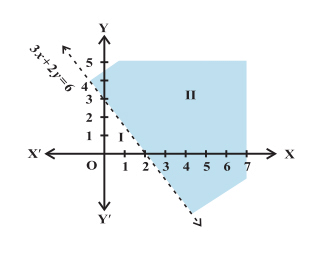
Question: Solve the following system of linear inequalities in two variables graphically.
x + y ≥ 5
x – y ≤ 3
Solution. To begin with, let’s draw a graph of the equation x + y = 5. Now, we determine if the point (0, 0), which is lying in the half-plane I, satisfies the inequality 1. We have,
x + y ≥ 5
⇒ 0 + 0 ≥ 5
Or, 0 ≥ 5 which is FALSE. Also, being a ‘Slack inequality, the points on the line represented by x + y = 5 satisfy the inequality 1. Hence, the solution lies in the half-plane II and includes the line.
Next, let’s draw a graph of the equation x – y = 3 on the same set of axes. Now, we determine if the point (0, 0), which is lying in the half-plane II, satisfies the inequality 2. We have,
x – y ≤ 3
⇒ 0 – 0 ≤ 3
Or, 0 ≤ 3 which is TRUE. Also, being a ‘Slack inequality, the points on the line represented by x – y = 3, satisfy the inequality 2. Hence, the solution lies in the half-plane II and includes the line. Look at the diagram below:
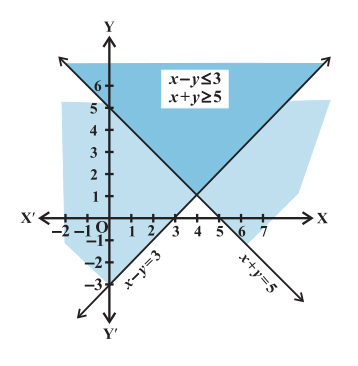
The solution of the system of linear inequalities in two variables x + y ≥ 5 and x – y ≤ 3 is the region common to the two shaded regions as shown above.
|
172 videos|476 docs|154 tests
|
FAQs on Linear Inequalities in One Variable and Two Variables - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the definition of linear inequalities in one variable? |  |
| 2. How can linear inequalities in one variable be solved algebraically and graphically? |  |
| 3. How are linear inequalities in two variables graphically represented and solved? |  |
| 4. What does it mean when any point in the Cartesian plane satisfies a linear inequality? |  |
| 5. Can linear inequalities be solved using graphical methods in addition to algebraic methods? |  |






















