Permutations | Mathematics (Maths) for JEE Main & Advanced PDF Download
What is Permutations and Combinations?
Imagine you go to an ice cream parlor, and they have five delicious flavors: Vanilla, Chocolate, Strawberry, Mint, and Caramel. Now, you want to order an ice cream cone with three different flavors.
Permutations come into play when the order in which you choose the flavors matters. In other words, if you want to create a unique sequence of flavors on your cone, we're talking about permutations.
Here's the deal: for each of your three scoops, you have five flavors to choose from. As you choose each flavor one after the other, the order in which you pick them creates a unique ice cream. That's where the magic of permutations steps in – the art of arranging items in a specific order.
Now, What if you didn't care about the order, but simply told the person in the ice cream parlour to make an ice cream for you. As the person adds one flavour after the other in any order, it creates different combinations.
 Ice Creams
Ice Creams
So with this understanding let's get ready to turn everyday decisions into thrilling mathematical adventures!
Fundamental Principle of Counting
The fundamental counting principle is a rule used to count the total number of possible outcomes in a situation.
It states that if there are n ways of doing something, and m ways of doing another thing after that, then there are n×m ways to perform both of these actions. In other words, when choosing an option for n and an option for m, there are n×m different ways to do both actions.
Permutation
Permutations involve arranging distinct objects in a specific order. Consider the word "ROSE," where each arrangement, such as ROSE, REOS, and so on, is unique. The order of the letters matters in permutations.
For instance, if we want to determine the number of 3-letter words that can be formed from the letters of the word "NUMBER" without repetition, we are counting the permutations of 6 different letters taken 3 at a time. Using the multiplication principle, the total number of arrangements is 6 × 5 × 4 = 120.
If repetition of letters was allowed, the count would be 6 × 6 × 6 = 216.
A permutation is an arrangement of objects in a definite order. Since we have already studied combinations, we can also interpret Permutations as ‘ordered combinations’.
Analysis
Let’s say we have a set of ‘n’ distinct objects, out of which we must choose ‘r’ objects. We can proceed in the following two ways of choosing the required objects:
• When the repetition of objects is allowed
• When the repetition of objects is not allowed
Case 1
When the repetition of objects is allowed, at every step of our choosing an object from the set of ‘n’ objects, we have all the ‘n’ choices available to us since we can make a choice multiple times. So, for choosing ‘r’ objects, we have n choices available to us ‘r’ times. Let us call the event of choosing an object as E:
n(E) = n (the number of ways in which E can take place)
Since this event is taking place ‘r’ times and the act of choosing an object from the available set is always independent of our other choices, we may invoke the Product Rule of Counting here. Using the fundamental principle then, we get,
n(E taking place ‘r’ times) = nr
This is the permutation formula for the number of permutations possible for the choice of ‘r’ objects from a set of ‘n’ distinct objects when repetition is allowed.
Case 2
In this case, when the repetition of objects is not allowed, we must be careful, not to choose a specific object more than once. Hence our choices after each event get reduced by one. For example, when we begin choosing our first object, we have all the ‘n’ choices available to us.
In the next event, however, we have ‘(n-1)’ objects available for choice, since we must not include the object that we have already chosen in the first step. Similarly, for the third step, we have ‘(n-2)’ objects available to us. Thus, from the Product Rule of Counting, we can get,
n(E) = n × (n – 1) × (n – 1) … (n – (r – 1))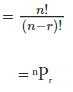
(notation for the number of permutations of r objects out of a set of n distinct objects)
A Specific Case
The number of permutations of ‘n’ objects from a set of ‘n’ distinct objects would be given by n!. For example, the number of ways in which you can jumble the alphabets of the word ‘flower’ is given by 6!. What if our reservoir set of ‘n’ objects has some repeated elements?
The formula can be derived in a similar manner to our derivation of the general formula, but with some important restrictions. You could try working it out yourself! But for the time being, let us just state and understand it. The number of permutations of ‘n’ objects where p1 objects are of one kind, p2 objects are of one other kind… till pk , is given by: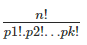
where clearly, p1 + p2 +p3 …..+ pk = n.
Example: The number of ways in which you can jumble the alphabets of the word ‘balloon’ is given by
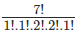
since the number count of different alphabets is given as:
n(occurrence of alphabet ‘b’)= 1
n(occurrence of alphabet ‘a’)= 1
Also, n(occurrence of alphabet ‘l’)= 2
n(occurrence of alphabet ‘o’)= 2
n(occurrence of alphabet ‘n’)= 1
Alternate Analysis of nPr
If you remember, we had also mentioned ‘ordered combinations’ as another interpretation of ‘permutations’. Let us look at the formula for the number of combinations of ‘r’ objects out of a set of ‘n’ objects:
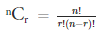
Let us take a specific combination of these number of different combinations. In permutations, the order of the chosen elements does matter; while in the combinations the order doesn’t matter. Thus, to arrive at the number of permutations, we must multiply the number of combinations by the number of possible permutations of each specific combination!
What is the number of permutations for a set of ‘r’ objects? It is simply r!, as we have discussed some time ago. Multiplying nCr by r!, we observe:
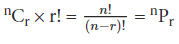
which is the same as the one we derived from our Product Rule of Counting. Therefore, the interpretation of ‘Permutations’ as ‘Ordered Combinations’ is correct!
Solved Example for You on Permutation Formula
Question: In a sports broadcasting company, the manager must pick the top three goals of the month, from a list of ten goals. In how many ways can the top three goals be decided?
Solution: Since the manager must decide the top three goals of the month; the order of the goals is very important! It decides the first-place winner, the runner-up, and the second runner-up. Thus, we can see that the problem is of permutation formula.
Picking up three goals from a list of ten:
Possible Permutations = 10P3 = 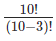 = 10 × 9 × 8 = 720
= 10 × 9 × 8 = 720
Therefore, there are 720 ways of picking the top three goals!
Fundamental Principles of Counting
1. Multiplication Principle
If first operation can be performed in m ways and then a second operation can be performed in n ways. Then, the two operations taken together can be performed in mn ways. This can be extended to any finite number of operations.
2. Addition Principle
If first operation can be performed in m ways and another operation, which is independent of the first, can be performed in n ways. Then, either of the two operations can be performed in m + n ways. This can be extended to any finite number of exclusive events.
Factorial
For any natural number n, we define factorial as n ! or n = n(n – 1)(n – 2) … 3 x 2 x 1 and 0!= 1!= 1
Permutation
Each of the different arrangement which can be made by taking some or all of a number of things is called a permutation.
Mathematically The number of ways of arranging n distinct objects in a row taking r (0 ≤ r ≤ n) at a time is denoted by P(n ,r) or npr
Properties of Permutation
Important Results on Permutation
- The number of permutations of n different things taken r at a time, allowing repetitions is nr.
- The number of permutations of n different things taken all at a time is nPn= n! .
- The number of permutations of n things taken all at a time, in which p are alike of one kind, q are alike of second kind and r are alike of third kind and rest are different is n!/(p!q!r!)
- The number of permutations of n things of which p1 are alike of one kind p2 are alike of second kind, p3 are alike of third kind,…, Pr are alike of rth kind such that p1 + p2 + p3 +…+pr = n is n!/P1!P2!P3!….Pr!
- Number of permutations of n different things taken r at a time,
when a particular thing is to be included in each arrangement is r.n – 1Pr – 1.
when a particular thing is always excluded, then number of arrangements = n – 1Pr - Number of permutations of n different things taken all at a time, when m specified things always come together is m!(n – m + 1)!.
- Number of permutations of n different things taken all at a time, when m specified things never come together is n! – m! x (n – m + 1)!.
Division into Groups
(i) The number of ways in which (m + n) different things can be divided into two groups which contain m and n things respectively [(m + n)!/m ! n !].
This can be extended to (m + n + p) different things divided into three groups of m, n, p things respectively [(m + n + p)!/m!n! p!].
(ii) The number of ways of dividing 2n different elements into two groups of n objects each is [(2n)!/(n!)2] , when the distinction can be made between the groups, i.e., if the order of group is important. This can be extended to 3n different elements into 3 groups is [(3n)!/((n!)3].
(iii) The number of ways of dividing 2n different elements into two groups of n object when no distinction can be made between the groups i.e., order of the group is not important is [(2n)!/2!(n!)2].
This can be extended to 3n different elements into 3 groups is [(3n)!/3!(n!)3].
The number of ways in which mn different things can be divided equally it into m groups, if order of the group is not important is [(mn)!/(n!)m m!].
(v) If the order of the group is important, then number of ways of dividing mn different things equally into m distinct groups is mn [(mn)!/(n!)m]
(vi) The number of ways of dividing n different things into r groups is [rn — rC1(r — 1)n + rC2(r — 2)n — rC3(r – 3)n + …].
(vii) The number of ways of dividing n different things into r groups taking into account the order of the groups and also the order of things in each group is n+r-1Pn = r(r + l)(r + 2) … (r + n – 1).
(viii) The number of ways of dividing n identical things among r persons such that each gets 1, 2, 3, … or k things is the coefficient of xn – r in the expansion of (1 + x + x2 + … + Xk-1)r.
Circular Permutation
In a circular permutation, firstly we fix the position of one of the objects and then arrange the other objects in all possible ways.
(i) Number of circular permutations at a time is (n -1)!. If clockwise taken as different. of n and different things taken anti-clockwise orders all are (n-1)!
(ii) Number of circular permutations of n different things taken all at a time, when clockwise or anti-clockwise order is not different 1/2(n – 1)!.
(iii) Number of circular permutations of n different things taken r at a time, when clockwise or anti-clockwise orders are take as different is nPr/r
(iv) Number of circular permutations of n different things taken r at a time, when clockwise or anti-clockwise orders are not different is nPr/2r.
(v) If we mark numbers 1 to n on chairs in a round table, then n persons sitting around table is n!.
|
172 videos|476 docs|154 tests
|
FAQs on Permutations - Mathematics (Maths) for JEE Main & Advanced
| 1. What is a permutation? |  |
| 2. How do you calculate the number of permutations? |  |
| 3. What is the difference between a permutation and a combination? |  |
| 4. How can permutations be used in real-life situations? |  |
| 5. Can permutations be used to solve probability problems? |  |