Basics of Straight Lines | Mathematics (Maths) for JEE Main & Advanced PDF Download
Introduction
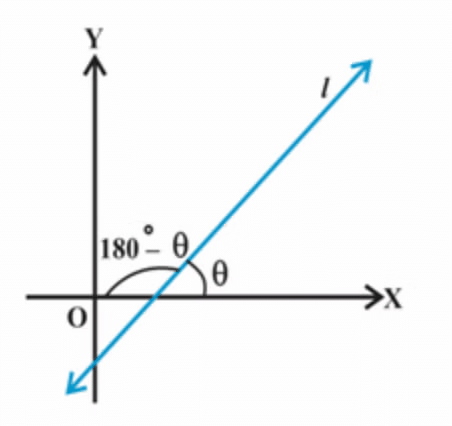
A line is considered as a geometrical shape with no breadth. It extends in both directions with no endpoints. It is a set of points and only has length. Lines can be parallel, perpendicular, intersecting or concurrent. A line in a coordinate plane forms two angles with the x-axis, which are supplementary. The angle (say) θ made by the line l with the positive direction of the x-axis and measured anti-clockwise is called the inclination of the line. Thus 0° ≤ θ ≤ 180°.
Slope of a Line
The basics of straight lines start with a slope.
- A slope is an inclined position. It forms a certain angle with the base.
- In coordinate geometry, if any line l makes an angle θ with the positive direction of the x-axis, it is called the Inclination of the line.
- The angle is measured in an anti-clockwise way. A slope of a line is the tangent of the inclination, θ i.e., tan θ. It is denoted as m.
Thus, the slope of a line: m = tan θ, where θ ≠ 90°.
1. When Coordinates of Any Points on the Lines Are Given
Imagine a line l with a slope θ.- Two points A (x1, y1) and B (x2, y2) lies on it.
- The angle of inclination can be acute or obtuse.
(i) Case 1: θ is acute
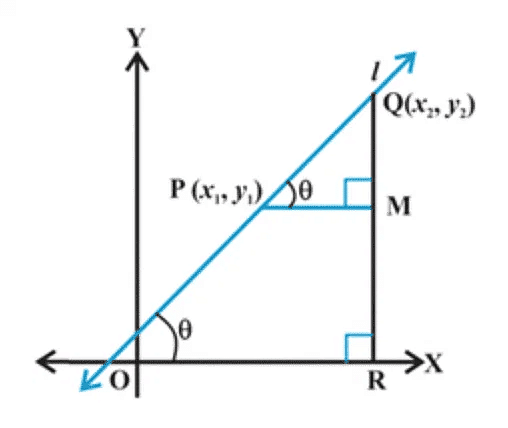
Here, ∠CAB = θ. The slope of the line, m = tan θ.
In ΔCAB, tan θ = CB/CA = (y2 − y1)/(x2 − x1).
Thus, m = tan θ = (y2 − y1)/(x2 − x1).
(ii) Case 2: θ is obtuse
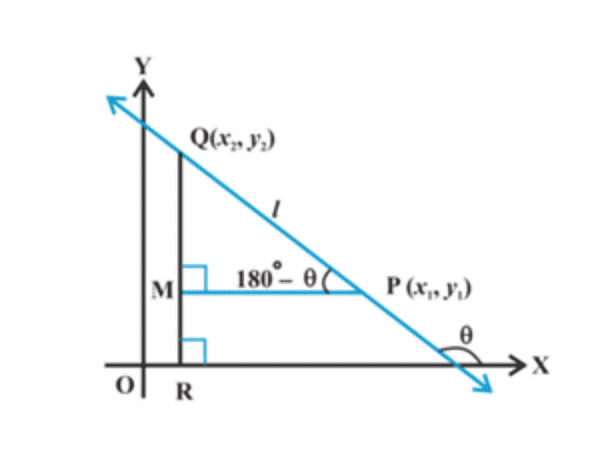
Here, ∠CAB =180° − θ.Slope of the line, m = tan θ = tan (180°− ∠CAB) = − tan ∠CAB
m = − CB/CA = − (y2 − y1)/(x1 − x2).
Thus, m = tan θ = (y2 − y1)/(x2 − x1).
2. Conditions for Parallelism of Lines in Terms of Slope
- Two lines are parallel if the distance between them at any point remains the same.
- It can also be inferred that the slopes of the two lines must be the same.
- Let two lines l1 and l2 have respective slopes m1 and m2 and angle of inclinations α and β.
The lines will be parallel if α = β i.e., m1 = m2 and tanα = tanβ
3. Conditions for Perpendicularity of Lines in Terms of Slopes
- Two lines are perpendicular if they intersect each other at an angle of 90°.
- Let two lines l1 and l2 have respective slopes m1 and m2 and angle of inclinations α and β.
- Here, α = β + 90°.
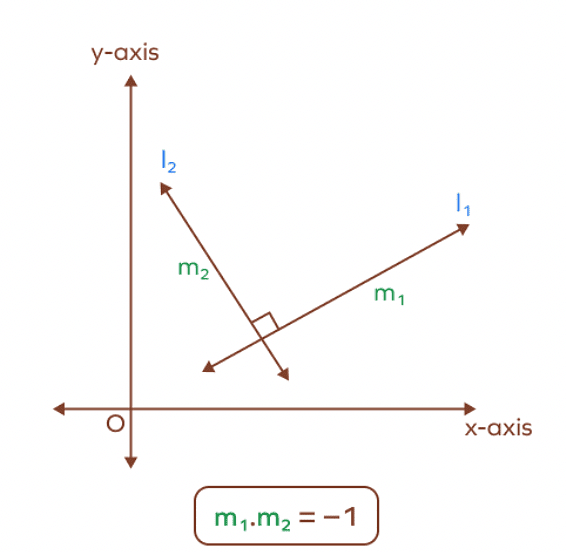
- tan α= tan (β + 90°) = − cot β = − 1/tan β
- or, m2 = −1 /m1 or m1m2 = −1
- The lines will be perpendicular if and only if m2 = −1/m1 or m1m2 = −1.
4. Angle Between Two Lines
- Above we get to know about parallel and perpendicular lines.
- How can we find out the angle between two intersecting lines (other than 90°)? Let two lines l1 and l2 have respective slopes m1 and m2 and angle of inclinations α1 & α2. Or, m1= tan α1 & m2 = tan α2
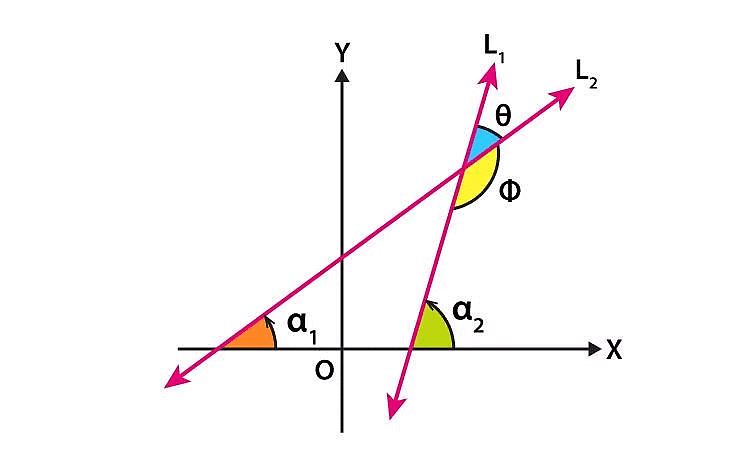
- From the property of angle:
θ = α1 − α2
tan θ = tan (α1 − α2)
= (tanα1 − tanα2)/ (1+ tanα1 tanα2)
= (m1−m2)/ (1+m1m2) - Φ = 180° − θ,
⇒ tan Φ = tan (180° − θ)
= − tan θ
= − (m1−m2) / (1+m1m2)
1 + m1m2 ≠ 0
5. Collinearity of Three Points
Three points are collinear if they all lie on the same line. Three points A(x1,y1), B(x2,y2) and C(x3,y3) are collinear iff slope of AB = slope of BC i.e., (y2 − y1)/(x2 − x1) = (y3 − y2)/(x3 − x2).
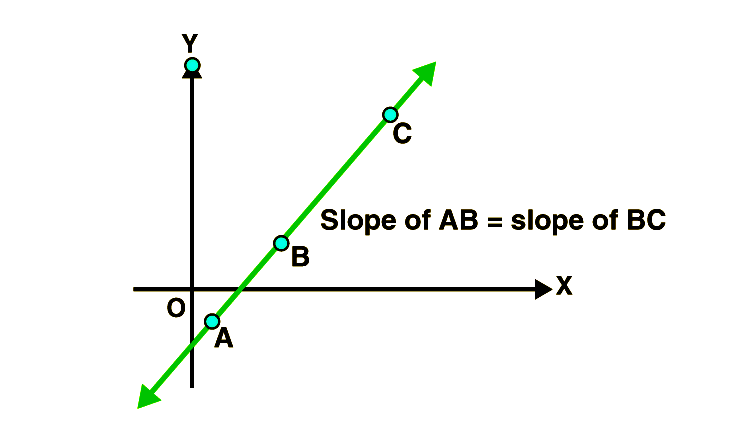
Solved Examples
Question 1: Find the slope of the line passing through the points (2, 3) and (5, 11)
Sol: Given points are (2, 3) and (5, 11)
So, to find the slope when two points are given, use the following formula
m = (y2 - y1)/(x2 - x1)
m = (11 - 3)/(5 - 2)
m = 8/3
So, the slope of the line passing through the points (2, 3) and (5, 11) is 8/3.
Question 2:Find the slope of the line passing through the points (4, 3) and (1, 5).
Sol: Slope of the line,
m = (y2 − y1)/(x2 − x1)
= (5 − 3) / (1 − 4)
= −2/3.
Question 3: Find the value of x, if the points (1, −1), (x, 1) and (6, 7) are collinear.
Sol: Three points are collinear if (y2 − y1)/(x2 − x1) = (y3 − y2)/(x3 − x2) .
Putting the values, we have,
(1 − (−1))/(x − 1)
= (7 − 1)/(6 − x) or, 2(6 − x)
= 6(x − 1).
Or,
x = 9/4.
Question 4: Find the angle between the following two lines: Line 1: 4x -3y = 8, Line 2: 2x + 5y = 4
Sol: Put 4x -3y = 8 into slope-intercept form so you can clearly identify the slope.
4x -3y = 8
3y = 4x - 8
y = 4x / 3 - 8/3
y = (4/3)x - 8/3
Put 2x + 5y = 4 into slope-intercept form so you can clearly identify the slope.
2x + 5y = 4
5y = -2x + 4y = -2x/5 + 4/5
y = (-2/5)x + 4/5
The slopes are 4/3 and -2/5 or 1.33 and -0.4.
It does not matter which one is m₁ or m₂.
You will get the same answer.
Let m₁ = 1.33 and m₂ = -0.4
tan θ = ± (m1 – m₂ ) / (1+ m₁m₂)
tan θ = ± (1.33 - (- 0.4)) / (1- (1.33)(-0.4))
tan θ = ± (1.73) / (1- 0.532)
tan θ = ± (1.73 ) / (0.468)
tan θ= 3.696θ
tan⁻¹ (3.69)
Question 5: Find the acute angle between y = 3x+1 and y = -4x+3
Sol: m₁= 3 and m₂ = -4
tan θ = ± (m1 – m2 ) / (1+ m₁m₂)
tan θ = ± (3-(-4) ) / (1+ 3(-4))
tan θ = ± (7 ) / (1+(-12))
tan θ = ± (7 ) / (-11)
tan θ = ± (7/11)
tan θ = 0.636θ
tan⁻¹ (0.636)
|
176 videos|582 docs|160 tests
|
FAQs on Basics of Straight Lines - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the slope of a line and how is it calculated? |  |
| 2. How do you graph a line given its slope and y-intercept? |  |
| 3. What are the differences between positive, negative, zero, and undefined slopes? |  |
| 4. Can you explain the concept of parallel and perpendicular lines in relation to slopes? |  |
| 5. How can you find the equation of a line when given its slope and a point on the line? |  |

















