Electrostatic Potential | Physics for JEE Main & Advanced PDF Download
What is Electrostatic Potential?
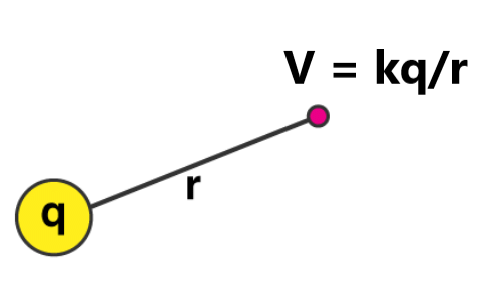
- The electrostatic potential of a point charge Q is given by V = kQ/r.
 Electric Potential
Electric Potential - Recall that the electric potential is defined as the potential energy per unit charge, i.e. V = PE/q
- The potential difference between two points ΔV is often called the voltage and is given by ΔV = VB − VA = ΔPE/q .
- The potential at an infinite distance is often taken to be zero.
- The case of the electric potential generated by a point charge is important because it is a case that is often encountered. A spherical sphere of charge creates an external field just like a point charge, for example.
- The equation for the electric potential due to a point charge is V = kQ/r , where k is a constant equal to 9.0×109 N⋅m2/C2.
- The electric potential tells you how much potential energy a single point charge at a given location will have. The electric potential at a point is equal to the electric potential energy (measured in joules) of any charged particle at that location divided by the charge (measured in coulombs) of the particle.
- Since the charge of the test particle has been divided out, the electric potential is a “property” related only to the electric field itself and not the test particle. Another way of saying this is that because PE is dependent on q, the q in the above equation will cancel out, so V is not dependent on q.
- The potential difference between two points ΔV is often called the voltage and is given by:
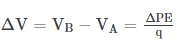
Electrostatic Potential Due to Point Charges
- Point charges, such as electrons, are among the fundamental building blocks of matter. Furthermore, spherical charge distributions (like on a metal sphere, see figure below) create external electric fields exactly like a point charge. The electric potential due to a point charge is, thus, a case we need to consider.
- Using calculus to find the work needed to move a test charge q from a large distance away to a distance of r from a point charge Q, and noting the connection between work and potential (W=–qΔV), it can be shown that the electric potential V of a point charge is
V = kQ/r (point charge)
where k is a constant equal to 9.0×109 N⋅m2/C2 . - The potential at infinity is chosen to be zero. Thus V for a point charge decreases with distance, whereas E for a point charge decreases with distance squared:
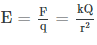
- The electric potential is a scalar while the electric field is a vector. Note the symmetry between electric potential and gravitational potential – both drop off as a function of distance to the first power, while both the electric and gravitational fields drop off as a function of distance to the second power.
Superposition of Electric Potential
- To find the total electric potential due to a system of point charges, one adds the individual voltages as numbers. The electric potential V is a scalar and has no direction, whereas the electric field E is a vector.
- To find the voltage due to a combination of point charges, you add the individual voltages as numbers. So for example, in the electric potential at point L is the sum of the potential contributions from charges Q1, Q2, Q3, Q4, and Q5 so that
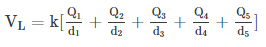 .
. - To find the total electric field, you must add the individual fields as vectors, taking magnitude and direction into account. This is consistent with the fact that V is closely associated with energy, a scalar, whereas E is closely associated with force, a vector.
- The summing of all voltage contributions to find the total potential field is called the superposition of electric potential. It is much easier to sum scalars than vectors, so often the preferred method for solving problems with electric fields involves the summing of voltages.
Key Terms
Vector: A directed quantity, one with both magnitude and direction; the between two points.
Scalar: A quantity that has magnitude but not direction; compare vector.
Superposition: The summing of two or more field contributions occupying the same space.
- We’ve seen that the electric potential is defined as the amount of potential energy per unit charge a test particle has at a given location in an electric field, i.e.
V = PE/q
We’ve also seen that the electric potential due to a point charge is V = kQ/r
where k is a constant equal to 9.0×109 N⋅m2/C2. The equation for the electric potential of a point charge looks similar to the equation for the electric field generated for a point particle: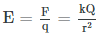
With the difference that the electric field drops off with the square of the distance while the potential drops off linearly with distance. This is analogous to the relationship between the gravitational field and the gravitational potential.
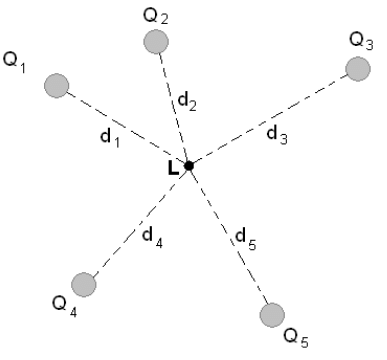 Superposition of Electric Potential: The electric potential at point L is the sum of voltages from each point charge (scalars)
Superposition of Electric Potential: The electric potential at point L is the sum of voltages from each point charge (scalars)Recall that the electric potential V is a scalar and has no direction, whereas the electric field E is a vector. To find the voltage due to a combination of point charges, you add the individual voltages as numbers. So for example, in the figure above the electric potential at point L is the sum of the potential contributions from charges Q1, Q2, Q3, Q4, and Q5 so that
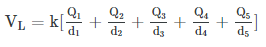
To find the total electric field, you must add the individual fields as vectors, taking magnitude and direction into account. This is consistent with the fact that V is closely associated with energy, a scalar, whereas E is closely associated with force, a vector.
The summing of all voltage contributions to find the total potential field is called the superposition of electric potential.
Summing voltages rather than summing the electric simplifies calculations significantly, since addition of potential scalar fields is much easier than addition of the electric vector fields. Note that there are cases where you might need to sum potential contributions from sources other than point charges; however, that is beyond the scope of this section.
Example.1 What Voltage Is Produced by a Small Charge on a Metal Sphere?
Solution.
- Charges in static electricity are typically in the nano coulomb (nC) to microcoulomb (µC) range. What is the voltage 5.00 cm away from the center of a 1-cm diameter metal sphere that has a −3.00nC static charge?
- As we have discussed in Electric Charge and Electric Field, charge on a metal sphere spreads out uniformly and produces a field like that of a point charge located at its center. Thus we can find the voltage using the equation V=kQ/r.
- Entering known values into the expression for the potential of a point charge, we obtain
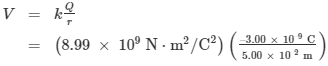
= –539 V. - Discussion: The negative value for voltage means a positive charge would be attracted from a larger distance, since the potential is lower—more negative—than at larger distances. Conversely, a negative charge would be repelled, as expected.
Potential due to an Electric Dipole
- The electric dipole is an arrangement that consists of two equal and opposite charges +q and -q separated by a small distance 2a.
- Electric dipole moment is represented by a vector p of magnitude 2qa and this vector points in the direction from -q to +q.
- To find electric potential due to a dipole consider charge -q is placed at point P and charge +q is placed at point Q as shown below in the figure.
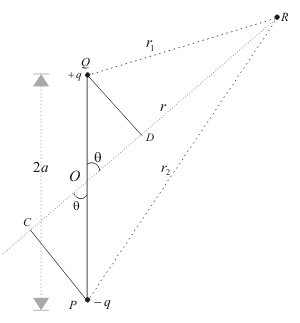 A Dipole
A Dipole - Since electric potential obeys the superposition principle so potential due to electric dipole as a whole would be sum of potential due to both the charges +q and -q. Thus
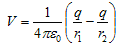
where r1 and r2 respectively are distance of charge +q and -q from point R. - Now draw line PC perpandicular to RO and line QD perpandicular to RO as shown in figure.
- From triangle POC
cosθ = OC/OP = OC/a
therefore OC=acosθ similarly OD=acosθ
Now ,
r1 = QR≅RD = OR-OD = r-acosθ
r2 = PR≅RC = OR+OC = r+acosθ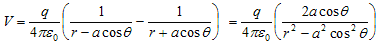
- Since magnitude of dipole is |p| = 2qa
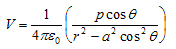
- If we consider the case where r>>a then
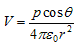
again since pcosθ= p·rˆ where, rˆ is the unit vector along the vector OR then electric potential of dipole is: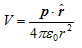
for r>>a - From above equation we can see that potential due to electric dipole is inversly proportional to r2 not ad 1/r which is the case for potential due to single charge.
Potential due to electric dipole does not only depends on r but also depends on angle between position vector r and dipole moment p.
Potential Due To A System Of Charges
- Consider a system of charges q1, q2,…, qn with position vectors r1, r2,…, r n relative to some origin. The potential V1 at P due to the charge q1 is:
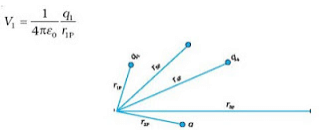 where r1P is the distance between q1 and P.
where r1P is the distance between q1 and P. - Similarly, the potential V2 at P due to q2 and due to q are given by
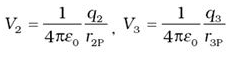 where r2P and r3P are the distances of P from charges q2 and q3, respectively; and so on for the potential due to other charges.
where r2P and r3P are the distances of P from charges q2 and q3, respectively; and so on for the potential due to other charges. - By the superposition principle, the potential V at P due to the total charge configuration is the algebraic sum of the potentials due to the individual charges
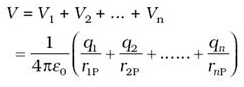
- The electric field outside the shell is as if the entire charge is concentrated at the centre. Thus, the potential outside the shell is given by:
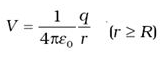 where q is the total charge on the shell and R its radius.
where q is the total charge on the shell and R its radius. - The electric field inside the shell is zero. This implies that potential is constant inside the shell (as no work is done in moving a charge inside the shell), and, therefore, equals its value at the surface, which is
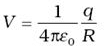
|
268 videos|740 docs|171 tests
|
FAQs on Electrostatic Potential - Physics for JEE Main & Advanced
| 1. What is electrostatic potential? |  |
| 2. How is electrostatic potential related to point charges? |  |
| 3. What is the superposition of electric potential? |  |
| 4. How is the potential calculated due to an electric dipole? |  |
| 5. How is the potential calculated for a system of charges? |  |





















