Seven Crystal Systems (Bravais Lattices) | Additional Study Material for JEE PDF Download
Bravais Lattices
Bravais (1848) showed from geometrical considerations that there are only seven shapes in which unit cells can exist.
These are
- Cubic
- Orthorhombic
- Rhombohedral
- Hexagonal
- Tetragonal
- Monoclinic
- Triclinic
Moreover, he also showed that there are basically four types of unit cells depending on the manner in which they are arranged in a given shape. These are:
- Primitive
- Body-Centered
- Face Centered
- End Centered
He also went on to postulate that out of the possible twenty-eight unit cells (i.e. seven shapes, four types in each shape = 28 possible unit cells), only fourteen actually would exist. These he postulated based only on symmetry considerations. These fourteen unit cells that actually exist are called Bravais Lattices.
Seven Crystal Systems
The seven crystal systems are given below.
➤ Cubic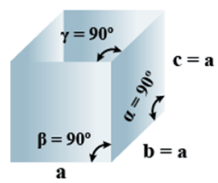
- Bravais Lattices
Primitive, face Centered, Body Centered = 3 - Parameters of Unit Cell
(i) Intercepts: a=b=c
(ii) Crystal angle: α = β = γ = 90o
Example: Pb, Hg, Ag, Au, Diamond, NaCl, ZnS
➤ Orthorhombic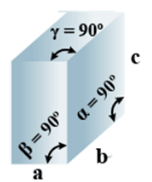
- Bravais Lattices:
Primitive, Face Centered, Body-Centered, End Centered = 4 - Parameters of Unit Cell:
(i) Intercepts: a ≠ b≠ c
(ii) Crystal angle: α = β = γ = 90o
Example: KNO2, K2SO4
➤ Tetragonal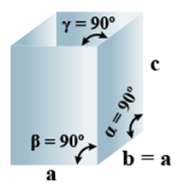
- Bravais Lattices:
Primitive, Body-Centered =2 - Parameters of Unit Cell:
(i) Intercepts: a = b≠ c
(ii) Crystal angle: α = β = γ = 90o
Example: TiO2, SnO2
➤ Monoclinic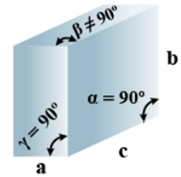
- Bravais Lattices
Primitive, End Centered =2 - Parameters of Unit Cell
(i) Intercepts: a ≠ b≠ c
(ii) Crystal angle: α = γ = 90o
Example: CaSO4.2H2O
➤ Triclinic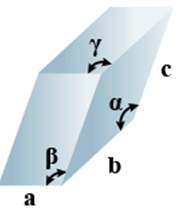
- Bravais Lattices
Primitive = 1 - Parameters of Unit Cell
(i) Intercepts: a ≠ b≠ c
(ii) Crystal angle: α ≠ β ≠ γ
Example: K2Cr2O7, CaSO4 5H2O
➤ Hexagonal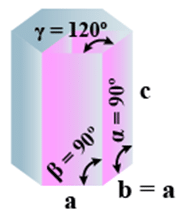
- Bravais Lattices
Primitive = 1 - Parameters of Unit Cell
(i) Intercepts: a = b≠ c
(ii) Crystal angle: α = β = 90o γ =120o
Example: Mg, SiO2, Zn, Cd
➤ Rhombohedral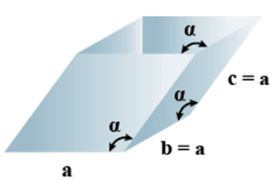
- Bravais Lattices:
Primitive = 1 - Parameters of Unit Cell
(i) Intercepts: a = b= c
(ii) Crystal angle: α = γ = 90o, β≠ 90o
Example: As, Sb, Bi, CaCO3
The table given below can be used to summarize types of lattice formation.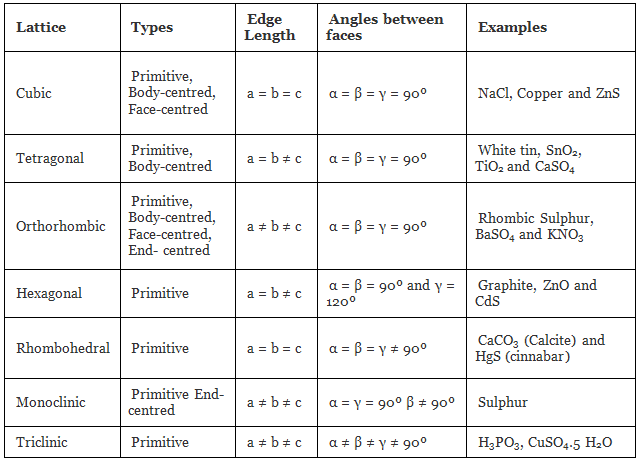
Q.1: Lithium borohydride crystallizes in an orthorhombic system with 4 molecules per unit cell. The unit cell dimensions are a = 6.8 Å, b = 4.4 Å and C = 7.2 Å. If the molar mass is 21.76 g. Calculate the density of the crystal.
Solution:
Since, Density,  Here z = 4, Av. No = 6.023 x 1023 &
Here z = 4, Av. No = 6.023 x 1023 &
Volume = V = a x b x c
= 6.8 x 108 x 4.4 x 108 x 7.2 x 108 cm3
= 2.154 x 1022 cm3
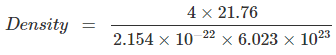
= 0.6708 gm/cm3
Q.2. An element crystallizes into a structure which may be described by a cubic type of unit cell having one atom in each corner of the cube and two atoms on one of its face diagonals. If the volume of this unit cell is 24 x 10-24 cm3 and density of the element is 7.20 gm/cm3, calculate no. of atoms present in 200 gm of the element.
Ans: Number of atoms contributed in one unit cell = one atom from the eight corners + one atom from the two face diagonals = 1+1 = 2 atoms
Mass of one unit cell = volume × its density
= 24 × 10–24 cm3 × 7.2 gm cm3
= 172.8 × 10–24 gm
∴ 172.8 10–24 gm is the mass of one – unit cell i.e., 2 atoms
∴ 200 gm is the mass = 2 × 200 / 172.8 × 10–24 atoms = 2.3148 × 1024 atoms
Q.3. Calculate the void fraction for the structure formed by A and B atoms such that A form hexagonal closed packed structure and B occupies 2/3 of octahedral voids. Assuming that B atoms exactly fitting into octahedral voids in the HCP formed by A.
Ans: Total volume of A atom = 6 × 4 / 3 πrA3
Total volume of B atoms = 4 × 4/3 πrA3
=4 × 4/3 π(0.414rA)3
Since rB/rA as B is in octahedral void of A
Volume of HCP = 24√2rA3
Packing fraction = 6 × 4/3 πrA3 + 4 × 4/3 π (0.414rA)3 / 24√2rA3 = 0.7756
Void fraction = 1-0.7756 = 0.2244
Q.4: An element with molar mass 2.7×10-2kg mol-1 forms a cubic unit cell with edge length 405 pm. If its density is 2.7×103kg-3, what is the nature of the cubic unit cell?
Ans: d = 2.7×103kg-3
M = 2.7×10 -2 kg mol-1
a= 405 pm = 405 X 10-12
NA= 6.023 X 1023
Using the formula
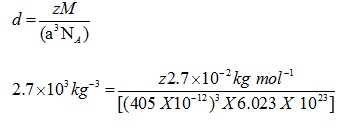
Z=4
Unit cell is fcc unit cell.
Volume of 54 g of the element = 0.054/(2.7 x 103) = 2 X 10-6
Number of unit cell in this volume = volume of 554 g of element/volume of each unit cell = 2 x 10-6/(405 x 10-12)3 = 3.012 x 1022
|
22 videos|163 docs|17 tests
|
FAQs on Seven Crystal Systems (Bravais Lattices) - Additional Study Material for JEE
| 1. What are Bravais lattices? |  |
| 2. How many crystal systems are there in Bravais lattices? |  |
| 3. What is the significance of Bravais lattices in the study of crystals? |  |
| 4. How do Bravais lattices relate to the JEE exam? |  |
| 5. Can you provide examples of real-life applications where knowledge of Bravais lattices is useful? |  |
















