Formula of a Compound, Number of Voids Filled & Calculations: Unit Cell Dimensions | Additional Study Material for JEE PDF Download
Formula of a Compound and Number of Voids Filled
 • The number of octahedral voids present in a lattice = The number of close packed particles.
• The number of octahedral voids present in a lattice = The number of close packed particles.
• The number of tetrahedral voids produced is twice this number.
• In ionic solids, the bigger ions i.e. anions forms close packed structure and the smaller ions i.e. cations occupy the voids.
• If the latter ion is small then tetrahedral voids are occupied, if bigger, then octahedral voids are occupied.
• In a compound, the fraction of octahedral or tetrahedral voids that are occupied depends upon the chemical formula of the compound.
• Close packed structures have both tetrahedral and octahedral voids.
Calculations Involving Unit Cells Dimensions
The help of geometry and attributes of unit cells, we can easily evaluate the volume of the unit cell. With volume and mass of atoms, we can also evaluate the density of the unit cell. A crystal lattice is represented in terms of unit cells; we can determine the density of crystal lattices by evaluating the density of unit cells.
Volume Density
Formula volume density of metal:
ρv = mass per unit cell/Volume per unit cell
Density of Unit Cell
A unit cell is a three-dimensional structure occupying one, two or more atoms. With the help of dimensions of unit cells, we can evaluate the density of the unit cell. To do so let’s consider a unit cell of edge length ‘a’, therefore the volume of the cell will be ‘a3’. Also, density is defined as the ratio of the mass of unit cell and volume of the unit cell.
Density of Unit Cell = mass of unit cell/Volume of unit cell......(1)
Mass of unit cell varies with number of atoms “n” and mass of a single atom “m”. Mathematically mass of unit cell is the product of number of atoms “n” and mass of one atom “m” i.e.
Mass of Unit Cell = n × m
Also from quantitative aspect of atoms, mass of one atom can be written in terms of Avogadro Number ( NA ) and molar mass of atom ( M), that is,
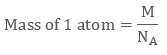
Volume of Unit Cell = a3
Placing the required values in equation 1 we get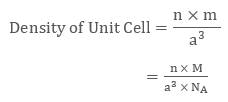
Therefore if we know molar mass of atom “M”, number of atoms “n”, the edge length of unit cell “a” we can evaluate the density of unit cell.
Example 1
The density of a face-centred unit cell is 6.23 g cm-3. Given the atomic mass of a single atom is 60, evaluate the edge length of the unit cell. (Take value of NA = 6.022 × 1023)
As the unit cell is a face-centred unit cell, a number of atoms will be 4. We have
n = 4 , M = 60 , NA = 6.022 × 1023 and d = 6.23 g cm-3
We know that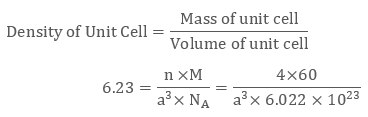
After evaluating we get the value of edge length of the cube to be 4 × 10-8 cm.
Example 2
KBr or potassium bromide has density 2.75 g cm-3. The edge length of its unit cell is 654 pm. Prove that KBr depicts face-centred cubic structure.
We have edge length of unit cell = 654 pm = 6.54 × 10-8 cm
Therefore volume of the cell = (6.54 ×10-8)3 cm3
Molar Mass of Potassium Bromide ( KBr) is 119 g/mol
Density of KBr = 2.75 g cm-3
We know that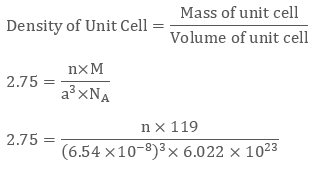
Evaluating we get value of n to be 3.09 ≈ 4
Since a number of atoms is 4 we can clearly say that KBr is a face-centred cubic structure.
|
22 videos|163 docs|17 tests
|
FAQs on Formula of a Compound, Number of Voids Filled & Calculations: Unit Cell Dimensions - Additional Study Material for JEE
| 1. What is the formula of a compound and how is it determined? |  |
| 2. How can we calculate the number of voids filled in a unit cell? |  |
| 3. What are the calculations involved in determining the unit cell dimensions? |  |
| 4. How can we determine the coordination number of an atom in a crystal lattice? |  |
| 5. What are some commonly used unit cells in crystal structures? |  |





















