Solved Examples for JEE: Sets | Mathematics (Maths) for JEE Main & Advanced PDF Download
Which of the following are sets? Justify your answer.
Q.1.
(a) The collection of all the months of a year beginning with letter M
(b) The collection of difficult topics in Mathematics.
Ans.
(a) Set
(b) Not a set
Q.2. Let A = {1, 3, 5, 7, 9}. Insert the appropriate symbol ∈ or ∈ in blank spaces
(i) 2 …A
(ii) 5 …A
Ans.
(i) ∉
(ii) ∈
Q.3. Write the set A = {x : x is an integer, –1 ≤ x < 4} in roster form
Ans. A = {–1, 0, 1, 2, 3}
Q.4. List all the elements of the set,
A = {× : × ϵ Z, - 1/2 < × < 11/2}
Ans. A = {0, 1, 2, 3, 4, 5}
Q.5. Write the set B = {3, 9, 27, 81} in set-builder form.
Which of the following are empty sets? Justify.
(a) A = {x : x ϵ N and 3 <x <4}
(b) B = {x : x ϵ N and X2 = x}
Ans. {x : x = 3n, n ϵ N and 1 ≤ n ≤ 4}
(a) Empty
(b) Non-empty
Q.6. Which of the following sets are finite or Infinite? Justify.
(a) The set of all the points on the circumference of a circle.
(b) B = {x : x ϵ N and x is an even prime number}
Ans.
(a) Infinite set
(b) Finite set
Q.7. Are sets A = {–2, 2}, B = {x : x ϵ Z, X2 –4 = 0} equal? Why?
Ans. Yes
Q.8. Write (–5,9] in set-builder form
Ans. {x : x ϵ R, –5 < x ≤ 9}
Q.9. Write {x : –3 ≤ x <7} as interval.
Ans. [–3, 7)
Q.10. If A = {1,3,5}, how many elements has P(A)?
Ans. 23 = 8
Q.11. Write all the possible subsets of A = {5,6}.
Ans. ∅, {5}, {6}, {5, 6}
Q.12. If A = {2,3,4,5}, B = {3,5,6,7}.Find
(a) A ∪ B
(b) A ∩ B
Ans.
(a) A ∪ B = {2, 3, 4, 5, 6, 7}
(b) A ∩ B = {3, 5}
Q.13. If A = {1, 2, 3, 6}, B = {1, 2, 4, 8} find B – A.
Ans. B – A = {4, 8}
Q.14. If A = {p, q}, B = {p, q, r}, is B a superset of A? Why?
Ans. Yes, because A is a subset of B
Q.15. Are sets A = {1,2,3,4}, B = {x : x ϵ N and 5 ≤ x ≤ 7} disjoint? Why?
Ans. Yes, because A ∩ B = ∅
Q.16. If X and Y are two sets such that n(X) = 19, n(Y) = 37 and n(X ∩ Y) = 12, find n(X ∪ Y).
Ans. n(X ∪ Y) = 44
Q.17. Describe the set in Roster form
{х : x is a two digit number such that the sum of its digit is 8}
Ans. {17, 26, 35, 44, 53, 62, 71, 80}
Q.18. Are the following pair of sets equal? Give reasons.
A = {x : x is a letter in the word FOLLOW}
B = {y : y is a letter in the word WOLF}
Ans.
A= {F, O, L, W}
B = {W, O, L, F}
Hence A = B
Q.19. Write down all the subsets of the set {1, 2, 3}
Ans. ∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}
Q.20. Let A = {1, 2, {3, 4, }, 5}. Is {{3, 4}} ⊂ A is incorrect. Give reason
Ans. {3, 4} is an element of set A, therefore {{3, 4}} is a set containing element {3, 4} which is a subset of set A.
Hence {{3, 4}} ⊂ A is correct.
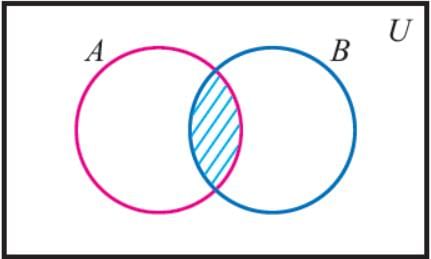
Q.21. Draw venn diagram for (A∩B)'
Ans. (A∩B)' = U - (A∩B)
 Q.22. Write the set in roster form A = The set of all letters in the word T R I G N O M E T R Y
Q.22. Write the set in roster form A = The set of all letters in the word T R I G N O M E T R Y
Ans. A = {T, R, I, G, N, O, M, E, Y}
Q.23. Are the following pair of sets equal? Give reasons
A, the set of letters in “ALLOY” and B, the set of letters in “LOYAL”.
Ans. A = {A, L, O, Y}
B = {L, O, Y, A}
Hence A = B
Q.24. Write down the power set of A, A = {1, 2, 3}
Ans. P(A) = {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}
Q.25. A = {1, 2, {3, 4}, 5} which is incorrect and why.
(i) {3, 4} ⊂ A
(ii) {3, 4} ϵ A
Ans. {3, 4} is an element of set A.
Hence {3, 4} ϵ A is correct and
{3, 4} ⊂ A is incorrect
Q.26. Fill in the blanks.
(i) A∪A' = --------
(ii) ( A')' = ---------
(iii) A∩A' = --------
Ans.
(i) U
(ii) A
(iii) ∅
Q.27. Write the set {1/2, 2/3, 3/4, 4/5, 5/6, 6/7} in the set builder form.
Ans. {x : x = n/n+1, where n is natural number and 1 ≤ n ≤ 6}
Q.28. Is set C = {x : x – 5 = 0} and E = {x : x is an integral positive root of the equation x2 – 2x – 15 = 0} are equal?
Ans. C= {5}
x2 - 2x - 15 = 0
x2 - 5x + 3x - 15 = 0
x(x - 5) +3(x - 5) = 0
(x - 5) (x + 3) = 0
x = 5
x = -3 [x = -3 reject]
∴ x = 5
E = {5}
Hence, C = E
Q.29. In a survey it is found that 21 people like product A, 26 people like product B and 29 like product C. If 14 people like product A and B, 14 people like product B and C, 12 people like product C and A, and 8 people like all the three products. Find how many like product C only?
Ans. Let A, B, and C be the set of people who like product A, product B, and product C respectively.
Accordingly,
n(A)=21,n(B)=26,n(C)=29,n(A∩B)=14,n(C∩A)=12,
n(B∩C)=14,n(A∩B∩C)=8
The Venn diagram for the given problem can be drawn as above.
It can be seen that number of people who like product C only is
=29–(4+8+6)=11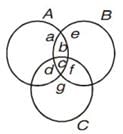 Q.30. A college awarded 38 medals in football, 15 in basketball and 20 in cricket. If these medals went to a total of 50 men and only five men got medals in all the three sports, how many received medals in exactly two of the three sports?
Q.30. A college awarded 38 medals in football, 15 in basketball and 20 in cricket. If these medals went to a total of 50 men and only five men got medals in all the three sports, how many received medals in exactly two of the three sports?
Ans. People who got medals in exactly two of the three sports.
Hint:
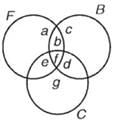 a, b, c, d, e, f, g – Number of elements in bounded region
a, b, c, d, e, f, g – Number of elements in bounded region
f = 5
a + b + f + e = 38
b + c + d + f = 15
e + d + f + g = 20
a + b + c + d + e + f + g = 50
we have to find b + d + e
Q.31. There are 200 individuals with a skin disorder, 120 had been exposed to the chemical C1, 50 to chemical C2, and 30 to both the chemicals C1 and C2. Find the number of individuals exposed to
(1) chemical C1 but not chemical C2
(2) chemical C2 but not chemical C1
(3) chemical C1 or chemical C2
Ans. A denote the set of individuals exposed to the chemical C1 and B denote the set of individuals exposed to the chemical C2
n(U) = 200, n(A) = 120, n(B) = 50, n(A∩B) = 30
(i) n(A-B) = n(A) – n(A∩B)
= 120 - 30 = 90
(ii) n(B-A) = n(B) – n(A B)
= 50 - 30 = 20
(iii) n(A∪B) = n(A)+ n(B)-n(A∩B)
= 120 + 50 - 30
= 140
Q.32. In a survey it was found that 21 peoples liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people like C and A, 15 people like B and C and 8 liked all the three products. Find now many liked product C only.
Ans. a + b + c + d = 21
b + c + e + f = 26
c + d + f + g = 29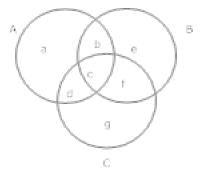 b + c = 14,c + f = 15, c + d = 12
b + c = 14,c + f = 15, c + d = 12
c = 8
d = 4, c = 8, f = 7, b = 6, g = 10, e = 5, a = 3
People who like product c only = g = 10
Q.33. A college awarded 38 medals in football, 15 in basketball and 20 in cricket. If these medals went to a total of 58 men and only three men got medal in all the three sports, how many received medals in exactly two of the three sports?
Ans. Let A, B and C denotes the set of men who received medals in football, basketball and cricket respectively.
n (A) = 38, n (B) = 15, n (C) = 20
n (A ∪ B ∪ C) = 58 and n (A ∩ B ∩ C) = 3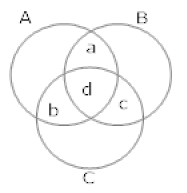 n (A ∪ B ∪ C) = n (A) + n (B) + n(C) – n (A ∩ B) – n (B ∩ C) – n (C ∩ A) + n (A ∩ B ∩ C)
n (A ∪ B ∪ C) = n (A) + n (B) + n(C) – n (A ∩ B) – n (B ∩ C) – n (C ∩ A) + n (A ∩ B ∩ C)
58 = 38 + 15 + 20 – (a + d ) – (d + c) – (b + d) + 3
18 = a + d + c + b + d
18 = a + b + c + 3d
18 = a + b + c + 3 * 3
9 = a + b + c
Q.34. In a survey of 60 people, it was found that 25 people read news paper H, 26 read newspaper T, 26 read newspaper I, 9 read both H and I, 11 read both H and T, 8 read both T and I, 3 read all three newspaper. Find
(i) The no. of people who read at least one of the newspapers.
(ii) The no. of people who read exactly one news paper.
Ans. a + b + c + d = 25
b + c + e + f = 26
c + d + f +g = 26
c + d = 9
b + c = 11
c + f = 8
c = 3
f = 5, b = 8, d = 6, c = 3, g = 12
e = 10, a = 8
(i) a + b + c + d + e + f + g = 52
(ii) a + e + g = 30
Q.35. These are 20 students in a chemistry class and 30 students in a physics class. Find the number of students which are either in physics class or chemistry class in the following cases.
(i) Two classes meet at the same hour
(ii) The two classes met at different hours and ten students are enrolled in both the courses.
Ans. Let C be the set of students in chemistry class and P be the set of students in physics class.
n (C) = 20, n (P) = 30
(i) C ∩ P = ϕ ⇒ n(C∩P) = 0
n (C ∪ P) = n (C) + n (P) + n (C ∩ P)
= 20 + 30 + 0
= 50
(ii) n (C ∩ P) = 10
n (C ∪ F) = n (C) + n (F) - n (C ∩ P)
= 20 + 30 - 10
= 40
Q.36. In a survey of 25 students, it was found that 15 had taken mathematics, 12 had taken physics and 11 had taken chemistry, 5 had taken mathematics and chemistry, 9 had taken mathematics and physics, 4 had taken physics and chemistry and 3 had taken all three subjects.
Find the no. of students that had taken
(i) only chemistry
(ii) only mathematics
(iii) only physics
(iv) physics and chemistry but mathematics
(v) mathematics and physics but not chemistry
(vi) only one of the subjects
(vii) at least one of three subjects
(viii) None of three subjects.
Ans. n(M) = a + b + d + e = 15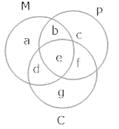 n (P) = b + c + e + f = 1 2
n (P) = b + c + e + f = 1 2
n(C) = d + e + f + g = 11
n (M ∩ P) = b + e =9
n (M ∩ C) = d + e = 5
n (P ∩ C) = e + f = 4
e = 3
so b = 6, d = 2, f = 1
a = 4, g = 5, c = 2
(i) g = 5
(ii) a = 4
(iii) c = 2
(iv) f = 1
(v) b = 6
(vi) g + a + c = 11
(vii) a + b + c + d + e + f + g + = 23
(viii) 25 - (a + b + c + d + e + f + g) = 25 - 23 = 2
Q.37. In a survey of 100 students, the no. of students studying the various languages were found to be English only 18, English but not Hindi 23, English and Sanskrit 8, English 26, Sanskrit 48, Sanskrit and Hindi 8, no language 24. Find
(i) How many students were studying Hindi?
(ii) How many students were studying English and Hindi?
Ans. ∪ = 100, a = 18
a + e = 23, e + g = 8
a + e + g + d = 26
e + g + f + c = 48
g + f = 8
so, e = 5, g = 3, d = 0, f = 5, c = 35
(i) d + g + f + b = 0 + 3 + 5 + 10 = 18
(ii) d + g = 0 + 3 = 3
|
209 videos|447 docs|187 tests
|
FAQs on Solved Examples for JEE: Sets - Mathematics (Maths) for JEE Main & Advanced
| 1. What is a set in mathematics? |  |
| 2. What is the cardinality of a set? |  |
| 3. What is the difference between a subset and a proper subset? |  |
| 4. What is the intersection of two sets? |  |
| 5. What is the union of two sets? |  |

















