GMAT Exam > GMAT Notes > Quantitative for GMAT > Solved Examples - Beyond Equations: Inequalities & Absolute Value
Solved Examples - Beyond Equations: Inequalities & Absolute Value | Quantitative for GMAT PDF Download
Section - 1
Draw the following inequalities on the number line provided:
Ques 1: 
Ans:
Ques 2: 
Ans:
Ques 3: 
Ans:
Ques 4: 
Ans:
Ques 5: 
Ans:
Section - 2
Ques 6: a is less than b.
Ans: a is less than b.
a < b
Ques 7: Five times x is greater than 10.
Ans: Five times x is greater than 10.
5x > 10
Ques 8: Six is less than or equal to 4x.
Ans: Six is less than or equal to 4x.
6 < 4x
Ques 9: The price of an apple is greater than the price of an orange.
Ans: The price of an apple is greater than the price of an orange.
Let a = the price of an apple
Let o = the price of an orange
a > o
Note: In this problem, we set up our variables to refer to prices— not the number of apples and oranges.
Ques 10: The total number of members is at least 19.
Ans: The total number of members is at least 19.
Let m — the number of members
m > 19
Section - 3
Solve the following inequalities.
Ques 11: x + 3 ≤- 2
Ans:
Ques 12: f - 4 ≤ 13
Ans:
Ques 13: 3b≥ 12
Ans:
Ques 14: -5x > 25
Ans:
Ques 15: -8<-4y
Ans:
Section - 4
Solve the following equations.
Ques 16: 2z + 4 ≥-18
Ans:
Ques 17: 7y - 3 ≤ 4y + 9
Ans:
Ques 18: b/5 ≤ 4
Ans:
Ques 19: d + 3/2<8
Ans:
Ques 20: 4x/ 7 ≤ 15 + x
Ans:
Section - 5
Solve the following inequalities.
Ques 21: 3 ( x - 7 ) ≥ 9
Ans:
Ques 22: 
Ans:
Ques 23: 2x - 1.5 > 7
Ans: 
Ques 24: 
Ans:
Ques 25: 
Ans:
The document Solved Examples - Beyond Equations: Inequalities & Absolute Value | Quantitative for GMAT is a part of the GMAT Course Quantitative for GMAT.
All you need of GMAT at this link: GMAT
|
115 videos|106 docs|113 tests
|
FAQs on Solved Examples - Beyond Equations: Inequalities & Absolute Value - Quantitative for GMAT
| 1. What is an inequality? |  |
Ans. An inequality is a mathematical statement that compares two quantities and expresses that one quantity is greater than, less than, or not equal to the other quantity. It uses symbols such as < (less than), > (greater than), ≤ (less than or equal to), ≥ (greater than or equal to), or ≠ (not equal to) to represent the relationship between the two quantities.
| 2. How do you solve an inequality? | |
Ans. To solve an inequality, you follow similar principles as solving equations. However, there are some differences depending on the type of inequality. For example, if there is a variable on both sides of the inequality, you need to isolate the variable on one side. When multiplying or dividing both sides by a negative number, you also need to reverse the inequality sign. It's important to carefully apply the rules and solve for the variable to find the range of values that satisfy the inequality.
| 3. What is absolute value? | |
Ans. Absolute value is a measure of the distance between a number and zero on a number line. It is always positive or zero. The absolute value of a number is represented by two vertical bars surrounding the number. For example, the absolute value of -5 is written as |-5|, which equals 5. The absolute value of a positive number is the number itself, while the absolute value of a negative number is the opposite of that number.
| 4. How do you solve absolute value inequalities? | |
Ans. To solve absolute value inequalities, you need to consider two cases. First, if the absolute value expression is greater than a positive number, you can remove the absolute value bars and write two separate inequalities, one without the absolute value and one with the opposite sign. Solve both inequalities separately to find the range of values that satisfy the inequality. Second, if the absolute value expression is less than a positive number, you can remove the absolute value bars and write a single inequality. Solve it to find the range of values that satisfy the inequality.
| 5. What are some real-life applications of inequalities and absolute value? | |
Ans. Inequalities and absolute value have numerous real-life applications. For instance, they are used in financial planning to determine spending limits or investment returns. In physics, inequalities are used to analyze motion and determine the range of possible values for variables. In computer science, inequalities are used in algorithms and optimization problems. Absolute value is often used in distance calculations, error analysis, or determining the magnitude of a vector. These concepts play a crucial role in various fields where comparing quantities or measuring distances is important.
Related Exams
About this Document
|
4.98/5 Rating |
|
Dec 22, 2024 Last updated |
Document Description: Solved Examples - Beyond Equations: Inequalities & Absolute Value for GMAT 2024 is part of Quantitative for GMAT preparation.
The notes and questions for Solved Examples - Beyond Equations: Inequalities & Absolute Value have been prepared according to the GMAT exam syllabus. Information about Solved Examples - Beyond Equations: Inequalities & Absolute Value covers topics
like and Solved Examples - Beyond Equations: Inequalities & Absolute Value Example, for GMAT 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Solved Examples - Beyond Equations: Inequalities & Absolute Value.
Introduction of Solved Examples - Beyond Equations: Inequalities & Absolute Value in English is available as part of our Quantitative for GMAT
for GMAT & Solved Examples - Beyond Equations: Inequalities & Absolute Value in Hindi for Quantitative for GMAT course.
Download more important topics related with notes, lectures and mock test series for GMAT
Exam by signing up for free. GMAT: Solved Examples - Beyond Equations: Inequalities & Absolute Value | Quantitative for GMAT
Description
Full syllabus notes, lecture & questions for Solved Examples - Beyond Equations: Inequalities & Absolute Value | Quantitative for GMAT - GMAT | Plus excerises question with solution to help you revise complete syllabus for Quantitative for GMAT | Best notes, free PDF download
Information about Solved Examples - Beyond Equations: Inequalities & Absolute Value
In this doc you can find the meaning of Solved Examples - Beyond Equations: Inequalities & Absolute Value defined & explained in the simplest way possible. Besides explaining types of
Solved Examples - Beyond Equations: Inequalities & Absolute Value theory, EduRev gives you an ample number of questions to practice Solved Examples - Beyond Equations: Inequalities & Absolute Value tests, examples and also practice GMAT
tests
|
Explore Courses for GMAT exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
practice quizzes
,Free
,Previous Year Questions with Solutions
,MCQs
,Summary
,Important questions
,Sample Paper
,mock tests for examination
,Solved Examples - Beyond Equations: Inequalities & Absolute Value | Quantitative for GMAT
,Exam
,Objective type Questions
,Solved Examples - Beyond Equations: Inequalities & Absolute Value | Quantitative for GMAT
,Viva Questions
,Solved Examples - Beyond Equations: Inequalities & Absolute Value | Quantitative for GMAT
,video lectures
,study material
,shortcuts and tricks
,ppt
,past year papers
,Extra Questions
,Semester Notes
;
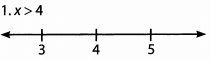
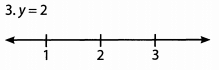
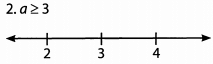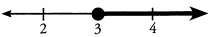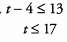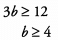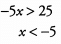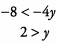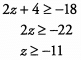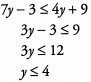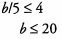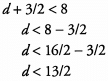Additional Information about Solved Examples - Beyond Equations: Inequalities & Absolute Value for GMAT Preparation
Solved Examples - Beyond Equations: Inequalities & Absolute Value Free PDF Download
The Solved Examples - Beyond Equations: Inequalities & Absolute Value is an invaluable resource that delves deep into the core of the GMAT exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Solved Examples - Beyond Equations: Inequalities & Absolute Value now and kickstart your journey towards success in the GMAT exam.
Importance of Solved Examples - Beyond Equations: Inequalities & Absolute Value
The importance of Solved Examples - Beyond Equations: Inequalities & Absolute Value cannot be overstated, especially for GMAT aspirants.
This document holds the key to success in the GMAT exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Solved Examples - Beyond Equations: Inequalities & Absolute Value Notes
Solved Examples - Beyond Equations: Inequalities & Absolute Value Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Solved Examples - Beyond Equations: Inequalities & Absolute Value.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Solved Examples - Beyond Equations: Inequalities & Absolute Value Notes on EduRev are your ultimate resource for success.
Solved Examples - Beyond Equations: Inequalities & Absolute Value GMAT Questions
The "Solved Examples - Beyond Equations: Inequalities & Absolute Value GMAT Questions" guide is a valuable resource for all aspiring students preparing for the
GMAT exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Solved Examples - Beyond Equations: Inequalities & Absolute Value on the App
Students of GMAT can study Solved Examples - Beyond Equations: Inequalities & Absolute Value alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Solved Examples - Beyond Equations: Inequalities & Absolute Value,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Solved Examples - Beyond Equations: Inequalities & Absolute Value is prepared as per the latest GMAT syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup