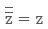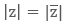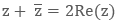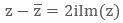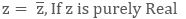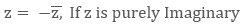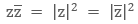Algebra of Complex Numbers | Basic Physics for IIT JAM PDF Download
What is Complex Number?
Complex Number is an algebraic expression including the factor i = √-1. These numbers have two parts, one is called as the real part and is denoted by Re(z) and other is called as the Imaginary Part. Imaginary part is denoted by Im(z) for the complex number represented by ‘z’.
Either of the part, real part or imaginary part, can be positive, negative, integer, fraction, decimal, rational, irrational or even zero. If only real part of any complex number ‘z’ is zero, i.e. Re(z) = 0, then these types of complex numbers are termed as ‘Purely Imaginary Number’. While if only imaginary part of any complex number ‘z’ is zero, that is. Im(z) = 0, then these are called as ‘Purely Real Numbers”.
Complex Number in its Cartesian form is expressed as z = a + ib or z = Re(z) + iIm(z).
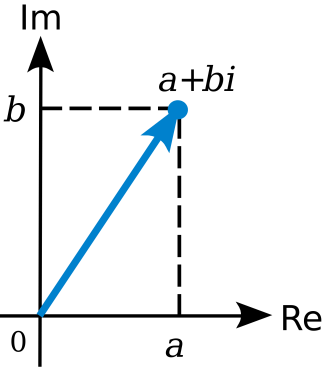
For Example, for a complex number, z = 2 + 3i, a = Re(z) = 2 and b = Im(z) = 3.
Complex Number in its Cartesian form is expressed as z = a + ib or z = Re(z) + iIm(z).
What are Imaginary Numbers in Math?
Imaginary Numbers are the real numbers multiplied with the imaginary unit ‘i’. ‘i’ (or ‘j’ in some books) in math is used to denote the imaginary part of any complex number. It helps us to clearly distinguish the real and imaginary parts of any complex number. Moreover, i is just not to distinguish but also has got some value.
i = √-1
Main application of complex numbers is in the field of electronics. In electronics, already the letter ‘i’ is reserved for current and thus they started using ‘j’ in place of i for the imaginary part.
Explain Algebra of Complex Numbers?
Let’s understand the different algebras of complex numbers one by one below:
- Equality of Complex Numbers
Two Complex numbers z1 and z2 are equal iff,
Condition 1) Re (z1) = Re (z2)
Condition 2) Im (Z1) = Im(z2)
So If, z1 = x + 3i and z2 = -2 + yi are equal, then as per above conditions,
Re(z1) = x and Re(z2) = -2, so x = -2
And Similarly
Im(z1) = 3 and Im(z2) = y, so y = 3 - Addition of Complex Numbers
Let z1 = a + ib and z2 = c + id, then the sum of this two complex numbers that is z1+ z2 calculated as:
z1+ z2 = (a + ib) + (c + id)
=(a + c) + i(b + d)
Therefore,
z1 + z2 = Re (z1+ z2) + Im(z1+ z2)
Addition of complex numbers can be another complex number.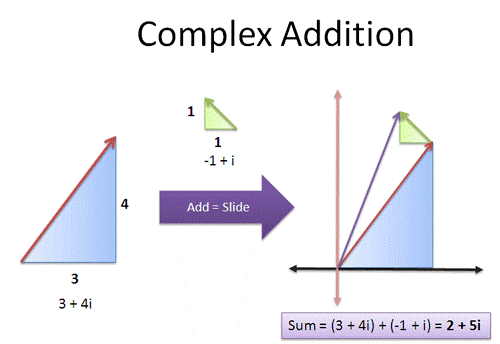
Example
Let z1= -1 + 4i and z2 = 8 + 2i,
Then z1+ z2 = (-1 + 8) + i(4 + 2) =7+ i6
ExampleAddition of complex numbers satisfy the following properties
- Closure Law: The sum of two complex numbers is another complex number, that is. if z1 + z2 where z1 and z2 are complex numbers, then z will also be a complex number
- Commutative Law: As per commutative law, for any two complex numbers z1 and z2, z1 + z2 = z2 + z1.
- Associative Law: For any three complex numbers say (z1+ z2 )+ z3 = z1+ (z2+ z3).
- Existence of Additive Identity: Additive identity also called as zero complex number is denoted as 0 (or 0 + i0), such that, for every complex number z, z + 0 = z.
- Existence of Additive Inverse: Additive inverse or negative of any complex number z, is a complex number whose both real and imaginary parts have the opposite sign. It is represented by –z and z + (-z) = 0
Difference of two Complex Numbers
- Let z1= a + ib and z2 = c + id, then the difference of this two complex numbers that is. z1 - z2 is calculated as:
z1- z2= (a + ib) - (c + id)
= (a – c) + i (b – d)
Therefore,
z1 - z2 = Re(z1 - z2 ) + Im(z1 - z2)
Difference of complex numbers can be another complex number
Example: Let z1= -1 + 4i and z2 = 8 + 2i,
Then z1- z2 =(-1 -8) + i(4 – 2) = -9 + i2
Difference of two complex numbers also satisfies the same properties as the addition of the two follows.
Multiplication of two Complex Numbers
- Let z1= a + ib and z2 = c + id, then the multiplication of this two complex numbers that is. z1× z2 is calculated as:
z1× z2 = (a + ib) ×(c + id)
z1×z2= (ac – bd) + i(ad + bc)
Therefore,
z1 × z2 = [Re(z1) Re(z2) – Im(z1) Im(z2)]+ i[Re(Z1) Im(z2) + Im(z2) Re(z2)]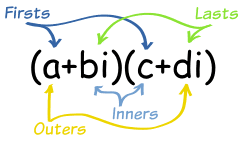 - Example: Let z1= -1 + 4i and z2 = 8 + 2i,
Then, z1 × z2 = (-8 -8) + i(-2 + 32) =-16 + i30
If k is any constant, then
kz = k(a + ib) = ka + ikb
Also, if k1 and k2 are any real constant, then
k(z1 + z2 )= kz1+ kz2
k1 (k2 z)=(k1 k2 )z
(k1+ k2 )z=k1 z+k2z
Multiplication of two complex numbers also possesses a few properties, let’s list them all here below:
- Closure Law: The product of any two complex numbers is another complex number, that is. if z = z1- z2 where z1 and z2 are complex numbers, then z will also be a complex number
- Commutative Law: As per commutative law, for any two complex numbers z1 and z2, z1 – z2 = z2 z1.
- Associative Law: For any three complex numbers say z1, z2 and z3. (z1 z2 ) z3 = z1 (z2 z3).
- Multiplicative Identity: Multiplicative Identity is denoted as 1 (or 1 + i0), such that, for every complex number z, z .1 = z.
- Multiplicative Inverse: For any non- zero complex number z,1/z or z-1 is called as ssthe multiplicative inverse as z,1/z = 1 If z = x + iy, then
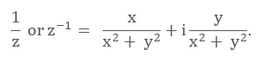
- Distributive Law: For any three complex numbers z1, z2 and z3 we have
z1 (z2+ z3 )= z1 z2+ z1 z3
(z1+ z2 ) z3 = z1 z3 + z2 z3
Division of two Complex Numbers
- Let z1 = a + ib and z2 = c + id, then the division of this two complex numbers that is z1/z2 is calculated as:
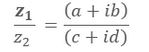
- On Rationalization:
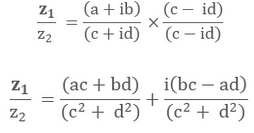
- Example:
Let z1 = -1 + 4i and z2 = 8 + 2i,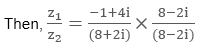
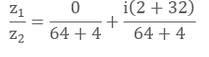
Power of i
Since i = √-1 or i = -1 which means i can be assumed as the solution of the equation x2 + 1 = 0 .i is called as Iota in complex numbers.
We can further formulate as,
So we can say now, i4n where n is any positive integer.
Also,
Also note that i + i2 + i3 + i4 = 0 or i4n+1 + i4n+2 + i4n+3 = 0 for any integer n.
Square root of a Complex Number
Let z1 = (a + ib) then the square root of a complex number z1, that is √z1 can be calculated as follows:
Assume, √z1 = x + iy
that is √(a + ib) = x + iy, Now squaring both the sides,
On simplification we get
(a + ib) = (x2- y2 )+ 2xyi
Now comparing both sides real and imaginary parts, we get
a = (x2- y2 ) and b = 2xy
Now using the below identity:
(x2- y2) = (x2 + y2) - 4xy, find the value of x2 + y2,
And then finally find the values of x2 and y2,we get
On further simplification, get the value of x and y by taking square root both sides,
Finally we get,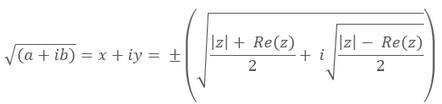
Example: Let’s find the square root of 8 – 6i.
Assume, √(8 – 6i) = x + iy On squaring and simplifying, we get
x2- y2 = 8 and 2xy = – 6
And finally we get, √(z1) = x+ iy = ± (3 – i)
What does the asterisk in Complex Numbers mean?
Asterisk (symbolically *) in complex number means the complex conjugate of any complex number.
Let z1 = x + iy is any complex number, then its complex conjugate is represented by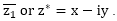 
We can also define the complex conjugate of any complex number as the complex number with same real part and same magnitude of imaginary part but with opposite sign as of given complex number.
Refer to the below table to understand it more clearly: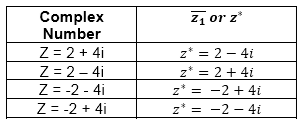
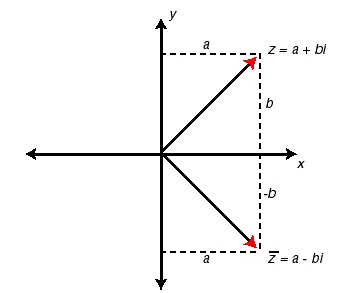
Also, note a few important properties of conjugate:
|
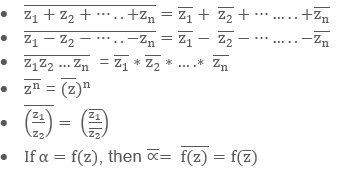
210 videos|156 docs|94 tests
|
FAQs on Algebra of Complex Numbers - Basic Physics for IIT JAM
| 1. What is a complex number? |  |
| 2. How are complex numbers used in algebra? | |
| 3. What is the algebra of complex numbers? | |
| 4. How are complex numbers used in physics? | |
| 5. What are some applications of complex numbers in physics? | |
|
4.78/5 Rating |
|
Dec 22, 2024 Last updated |
|
Explore Courses for Physics exam
|
|
shortcuts and tricks
,MCQs
,Algebra of Complex Numbers | Basic Physics for IIT JAM
,ppt
,Sample Paper
,study material
,Extra Questions
,Objective type Questions
,mock tests for examination
,practice quizzes
,Viva Questions
,Important questions
,Exam
,video lectures
,Free
,past year papers
,Summary
,Algebra of Complex Numbers | Basic Physics for IIT JAM
,Algebra of Complex Numbers | Basic Physics for IIT JAM
,Semester Notes
,Previous Year Questions with Solutions
;
Algebra of Complex Numbers Free PDF Download
Importance of Algebra of Complex Numbers
Algebra of Complex Numbers Notes
Algebra of Complex Numbers Physics Questions
Study Algebra of Complex Numbers on the App
|
© EduRev
|
Education Revolution
|
|
