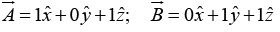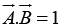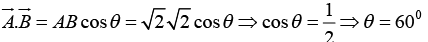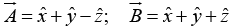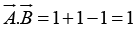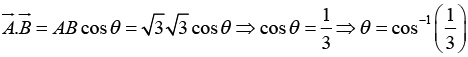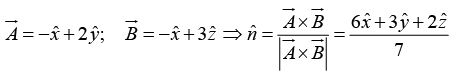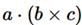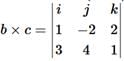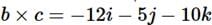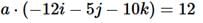Vector Algebra | Basic Physics for IIT JAM PDF Download
| Table of contents |

|
| Introduction |

|
| Vector Operations |

|
| Vector Algebra: Component Form |

|
| Triple Products |

|
 Vectors
Vectors
Introduction
Vector quantities have both direction as well as magnitude such as velocity, acceleration, force and momentum etc. We will use 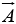 for any general vector and its magnitude by |
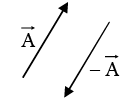
for any general vector and its magnitude by | |. In diagrams vectors are denoted by arrows: the length of the arrow is proportional to the magnitude of the vector, and the arrowhead indicates its direction. Minus
|. In diagrams vectors are denoted by arrows: the length of the arrow is proportional to the magnitude of the vector, and the arrowhead indicates its direction. Minus 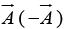 is a vector with the same magnitude as
is a vector with the same magnitude as 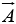 but of opposite direction.
but of opposite direction.
Vector Operations
We define four vector operations: addition and three kinds of multiplication.
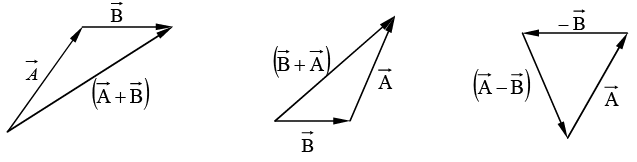
(i) Addition of two vectors
Place the tail of 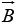 at the head of
at the head of 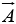 ; the sum,
; the sum,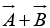 , is the vector from the tail of
, is the vector from the tail of 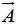 to the head of
to the head of 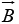 .
.
Addition is commutative: 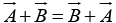
Addition is associative: 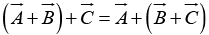
To subtract a vector, add its opposite: 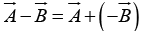
(ii) Multiplication by scalar
Multiplication of a vector by a positive scalar a, multiplies the magnitude but leaves the direction unchanged. (If a is negative, the direction is reversed.) Scalar multiplication is distributive: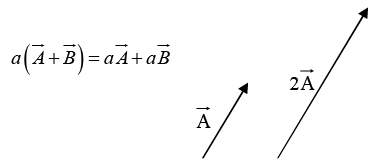
(iii) Dot product of two vectors
The dot product of two vectors is define by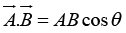
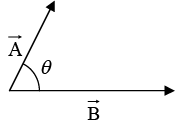
where θ is the angle they form when placed tail to tail. Note that 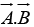 is itself a scalar. The dot product is commutative,
is itself a scalar. The dot product is commutative,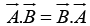
and distributive, 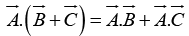
Geometrically 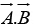 is the product of A times the projection of
is the product of A times the projection of 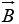 along
along 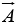 (or the product of B times the project ion of
(or the product of B times the project ion of 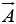 along
along 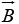 ).
).
If the two vectors are parallel, 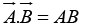
If two vectors are perpendicular, then 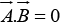
Law of cosines
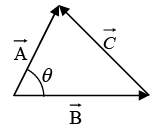
Let 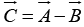 and then calculate dot product of
and then calculate dot product of 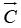 with itself.
with itself.
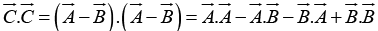
C2 = A2 + B2 - 2AB cosθ
(iv) Cross product of two vectors
The cross product of two vectors is define by
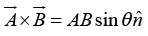
 where
where 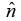 is a unit vector(vector of length 1) point ing perpendicular to the plane of
is a unit vector(vector of length 1) point ing perpendicular to the plane of  and
and 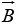 . Of course there are two directions perpendicular to any plane “in” and “out.” The ambiguity is resolved by the right-hand rule: let your fingers point in the direction of first vector and curl around (via the smaller angle) toward the second; then your thumb indicates the direction of
. Of course there are two directions perpendicular to any plane “in” and “out.” The ambiguity is resolved by the right-hand rule: let your fingers point in the direction of first vector and curl around (via the smaller angle) toward the second; then your thumb indicates the direction of 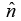 . (In figure
. (In figure 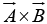 points into the page;
points into the page; 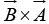 points out of the page)
points out of the page)
The cross product is distributive,
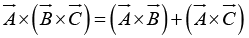
but not commutative.
In fact, 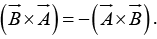
Geometrically, |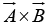 | is the area of the parallelogram generated by
| is the area of the parallelogram generated by 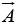 and
and 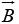 . If two vectors are parallel, their cross product is zero.
. If two vectors are parallel, their cross product is zero.
In particular 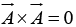 for any vector
for any vector  .
.
Vector Algebra: Component Form
Let 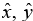 and
and 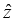 be unit vectors parallel to the x, y and z axis, respectively. An arbitrary vector
be unit vectors parallel to the x, y and z axis, respectively. An arbitrary vector 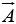 can be expanded in terms of these basis vectors
can be expanded in terms of these basis vectors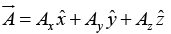
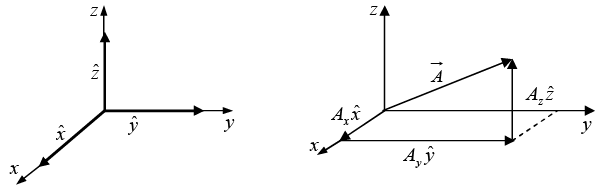
The numbers Ax , Ay , and Az are called component of 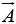 ; geometrically, they are the projections of
; geometrically, they are the projections of 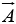 along the three coordinate axes.
along the three coordinate axes.
(i) Rule: To add vectors, add like components.
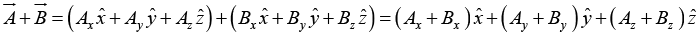
(ii) Rule: To multiply by a scalar, multiply each component.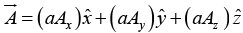
Because 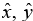 and
and 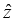 are mutually perpendicular unit vectors
are mutually perpendicular unit vectors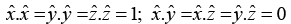
Accordingly, 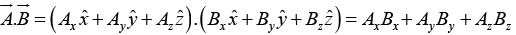
(iii) Rule: To calculate the dot product, multiply like components, and add.
In particular, 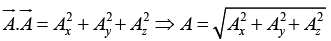
Similarly,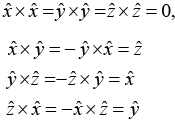
(iv) Rule: To calculate the cross product, form the determinant whose first row is  ,
, , whose second row is
, whose second row is 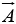 (in component form), and whose third row is
(in component form), and whose third row is 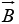 .
.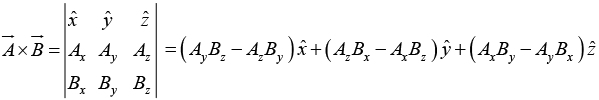
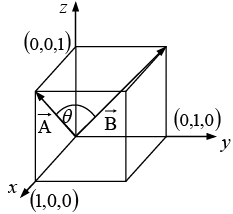
Example 1: Find the angle between the face diagonals of a cube.
Solution: The face diagonals
and
are
So, ⇒
Also, ⇒
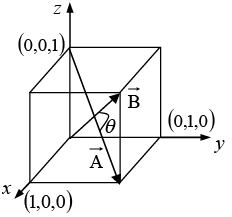
Example 2: Find the angle between the body diagonals of a cube.
Solution: The body diagonals
and
are
So, ⇒
Also,
⇒
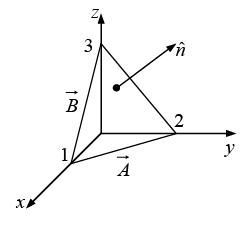
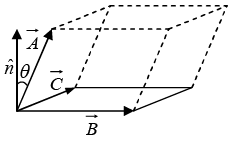
Example 3: Find the components of the unit vector nˆ perpendicular to the plane shown in the figure.
Solution: The vectors
and
can be defined as
Triple Products
Since the cross product of two vectors is itself a vector, it can be dotted or crossed with a third vector to form a triple product.(i) Scalar triple product:
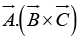
Geometrically 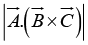 is the volume of the parallelepiped generated by
is the volume of the parallelepiped generated by 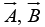 and
and 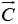 , since
, since 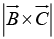 is the area of the base, and
is the area of the base, and 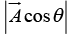 is the altitude. Evidently,
is the altitude. Evidently,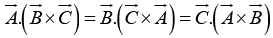 In component form
In component form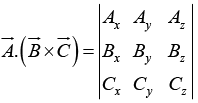 Note that the dot and cross can be interchanged:
Note that the dot and cross can be interchanged: 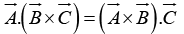
(ii) Vector triple product: 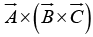
The vector triple product can be simplified by the so-called BAC-CAB rule:
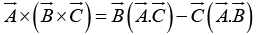
|
217 videos|156 docs|94 tests
|
FAQs on Vector Algebra - Basic Physics for IIT JAM
| 1. What are the basic operations that can be performed on vectors? |  |
| 2. How do you express vectors in component form? |  |
| 3. What is the significance of the triple product in vector algebra? |  |
| 4. How can vector operations be applied in physics? |  |
| 5. What is the difference between scalar and vector quantities? |  |