Stokes's theorem - IIT JAM PDF Download

For ω a differential (k-1)-form with compact support on an oriented K-dimensional manifold with boundary M,

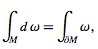(1)

where dω is the exterior derivative of the differential form ω. When M is a compact manifold without boundary, then the formula holds with the right hand side zero.

Stokes' theorem connects to the "standard" gradient, curl, and divergence theorems by the following relations. If f is a function on R³, 

grad(f)=c^-1df,    (2)

where c:R³ →R³ (the dual space) is the duality isomorphism between a vector space and its dual, given by the Euclidean inner product on R³. If f is a vector field on a R³,

div (f) = *d* c(f),    (3)

where * is the Hodge star operator. If f is a vector field on R³, 

curl(f)=c^-1*dc(f).     (4)

With these three identities in mind, the above Stokes' theorem in the three instances is transformed into the gradient, curl, and divergence theorems respectively as follows. If f is a function on R³ and ϒ is a curve in R³, then

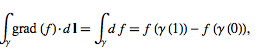(5)

which is the gradient theorem. If f:R³→R³ is a vector field and M an embedded compact 3-manifold with boundary in R³, then

   (6)

which is the divergence theorem. If f is a vector field and M is an oriented, embedded, compact 2-manifold with boundary in R³, then 

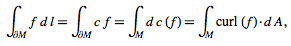  (7) 

which is the curl theorem.

de Rham cohomology is defined using differential k-forms. When N is a submanifold (without boundary), it represents a homology class. Two closed forms represent the same cohomology class if they differ by an exact form, ω₁, ω₂ =dn. Hence,

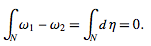 (8)

Therefore, the evaluation of a cohomology class on a homology class is well-defined. Physicists generally refer to the curl theorem 

 (9)

as Stokes' theorem.

A special case of Stokes' theorem in which F is a vector field and M is an oriented, compact embedded 2-manifold with boundary in R³, and a generalization of Green's theorem from the plane into three-dimensional space. The curl theorem states

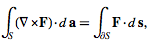 (10)

where the left side is a surface integral and the right side is a line integral.
There are also alternate forms of the theorem. If 

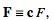 (11)

then 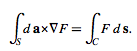 (12)

and if 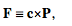 (13)

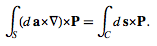then  (14)