Operations on Complex Numbers | Algebra - Mathematics PDF Download
The Complex Algebra
In basic algebra of numbers, we have four operations namely – addition, subtraction, multiplication and division. As we will see in a bit, we can combine complex numbers with them. Let z1 and z2 be any two complex numbers and let, z1 = a+ib and z2 = c+id.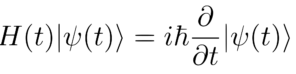
Example: Schrodinger Equation which governs atoms is written using complex numbers
Addition and Subtraction of Imaginary Numbers
The addition of two complex numbers is defined as:
z1+z2 = (a+ib) ± (c+id) = (a+c) ± i(b+d)
Which gives another complex number whose real part is Re(z1) + Re(z2) = a + c and imaginary part of the new complex number = Im(z1) + Im(z2) = b + d. For example, on adding 2 and 3 + 4i, we can write 2 as 2 + 0*i and therefore, 2 + (3+4i) = (2+3) + i(0+4) = 5 + i.4
Properties of Addition and Subtraction
The addition or subtraction of complex numbers always results in a complex number. This operation follows the following rules *:
• The Closure law or the closure property: Addition or subtraction of complex numbers yields a complex number.
• The Commutative Law: Any two complex numbers commute with respect to addition or subtraction i.e. z1+z2=z2+z1,
• The Associative Law: If z1, z2, z3 are any three complex numbers then we have (z1+z2)+z3 = z1+(z2+z3)
• Additive Identity: Additive identity is such a complex number that will return the original number upon addition. For example for real numbers, 0 is the additive identity. Similarly, we see for complex numbers 0 + i.0 is the additive identity (We will just denote it by 0).
• Additive Inverse: For each operation involving the combination of complex numbers through addition or subtraction, there exists an inverse such that the addition or subtraction of a complex number with it, yields the additive identity. For every complex number z = a + ib, there exists a complex number – z = -a + i(-b) such that z + (-z) = 0 or the additive identity.
*These properties are very important. Any collection of mathematical objects (set) that follows the above-mentioned properties under an operation (here ‘+’ and ‘-‘) is said to be a Group. You will learn about Groups and Fields in higher algebra. Groups are used in the development of almost all modern scientific theories.
Complex Numbers are used to study the shapes of atoms and molecules
Multiplication and Division of Imaginary Numbers
The multiplication of two complex numbers is defined as:
(z1×z2) = (a+ib) × (c+id) = (ac–bd)+i(ad + bc)
Similar z1/z2 = z1 × 1/z2; we can use cross multiplication and the multiplication of complex numbers for division. The multiplication and division also form a group i.e. they have similar properties as addition and subtraction.
Properties of Multiplication And Addition
• The Closure law or the closure property: (z1×z2) is always a complex number.
• The Commutative Law: If z1 and z2 are two complex numbers the, (z,×z2) = (z2×z1)
• The Associative Law: If z1, z2, z3 are any three complex numbers then we have (z1×z2) × z3 = z1 × (z2×z3).
• Multiplicative Identity: For each complex number there exists a number 1 + i.0 such that z×( 1 + i.0) = z ; where z is a complex number.
• Multiplicative Inverse: For each complex number z there exists a number 1/z such that z×(1/z) = 1 + i.0. This is known as the Multiplicative Inverse.
• The Distributive Law: If z1, z2, z3 are any three complex numbers then we have z1 × (z2 + z3) = z1 z2 + z1 z3 (Left distributive law) and ( z1 + z2 ) × z3 = z1 z3 + z1 z2
The division also follows the same properties.
Solved Examples For You
Question: Find the smallest integer n such that 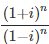 is
is
A) 16
B) 12
C) 8
D) 4
Solution:(D). Here we use a little trick. We have 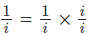
Remember that i×i = -1 and therefore we have, 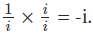 . Hence using it in the denominator of the given equation, we have:
. Hence using it in the denominator of the given equation, we have: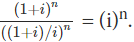 Hence, for (i)n = 1, n should be atleast 4.
Hence, for (i)n = 1, n should be atleast 4.
|
181 videos|58 docs
|
FAQs on Operations on Complex Numbers - Algebra - Mathematics
| 1. What are complex numbers? |  |
| 2. How do you add complex numbers? |  |
| 3. Can you subtract complex numbers? |  |
| 4. How do you multiply complex numbers? |  |
| 5. How do you divide complex numbers? |  |
















