Problems for Practice - 1 | Algebra - Mathematics PDF Download
For each of the following power series determine the interval and radius of convergence.
1. For the following power series determine the interval and radius of convergence.
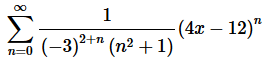
Solution. Okay, let’s start off with the Ratio Test to get our hands on L.
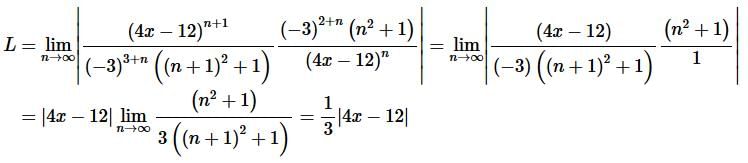
Step 2. So, we know that the series will converge if,
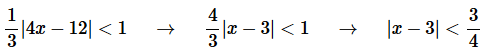
Step 3. So, from the previous step we see that the radius of convergence is 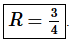
Step 4. Now, let’s start working on the interval of convergence. Let’s break up the inequality we got in Step 2.
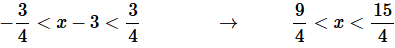
Step 5. To finalize the interval of convergence we need to check the end points of the inequality from Step 4.
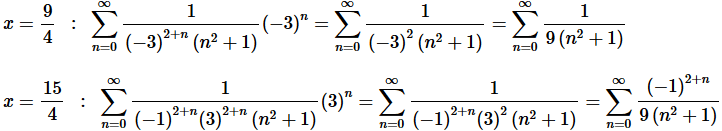
Now, we can do a quick Comparison Test on the first series to see that it converges and we can do a quick Alternating Series Test on the second series to see that is also converges. We’ll leave it to you to verify both of these statements.
Step 6. The interval of convergence is below and for summary purposes the radius of convergence is also shown.
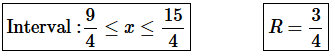
2. For the following power series determine the interval and radius of convergence.
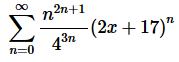
Solution. Okay, let’s start off with the Root Test to get our hands on L.
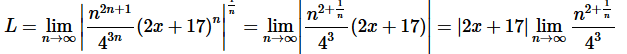
Okay, we can see that , in this case, L will be infinite provided 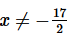 and so the series will diverge for
and so the series will diverge for 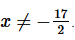 We also know that the power series will converge for
We also know that the power series will converge for 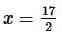 (this is the value of a for this series!).
(this is the value of a for this series!).
Step 2. Therefore, we know that the interval of convergence is 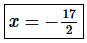 and the radius of convergence is
and the radius of convergence is 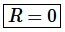
3. For the following power series determine the interval and radius of convergence.
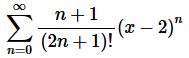
Solution. Okay, let’s start off with the Ratio Test to get our hands on L.
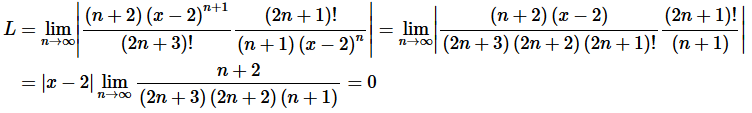 Okay, we can see that , in this case, L=0 for every x.
Okay, we can see that , in this case, L=0 for every x.
Step 2. Therefore, we know that the interval of convergence is 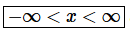 and the radius of convergence is
and the radius of convergence is 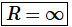
4. For the following power series determine the interval and radius of convergence.
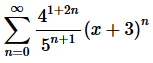
Solution. Okay, let’s start off with the Ratio Test to get our hands on L.
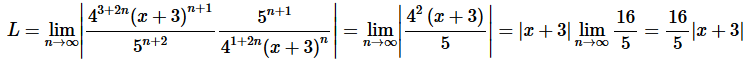
Step 2. So, we know that the series will converge if,
Step 3. So, from the previous step we see that the radius of convergence is 
Step 4. Now, let’s start working on the interval of convergence. Let’s break up the inequality we got in Step 2.
Step 5. To finalize the interval of convergence we need to check the end points of the inequality from Step 4.
Now,
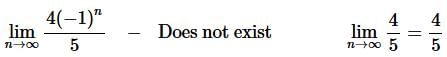
Therefore, each of these two series diverge by the Divergence Test.
Step 6. The interval of convergence is below and for summary purposes the radius of convergence is also shown.
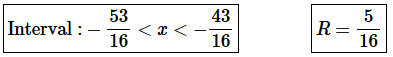
5. For the following power series determine the interval and radius of convergence.
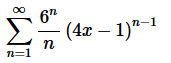
Solution. Okay, let’s start off with the Ratio Test to get our hands on L.
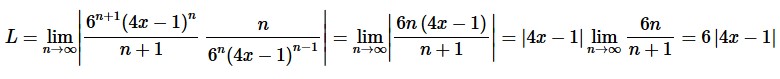
Step 2. So, we know that the series will converge if,
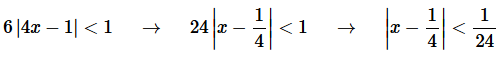
Step 3. So, from the previous step we see that the radius of convergence is 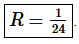
Step 4. Now, let’s start working on the interval of convergence. Let’s break up the inequality we got in Step 2.

Step 5. To finalize the interval of convergence we need to check the end points of the inequality from Step 4.
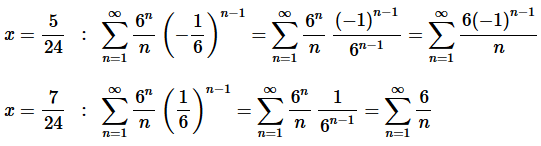
Now, the first series is an alternating harmonic series which we know converges (or you could just do a quick Alternating Series Test to verify this) and the second series diverges by the p-series test.
Step 6. The interval of convergence is below and for summary purposes the radius of convergence is also shown.
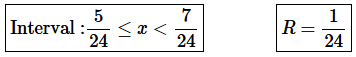
|
161 videos|58 docs
|
FAQs on Problems for Practice - 1 - Algebra - Mathematics
| 1. What are the different branches of mathematics? |  |
| 2. How can I improve my problem-solving skills in mathematics? |  |
| 3. What is the importance of mathematics in everyday life? |  |
| 4. How can I overcome math anxiety? |  |
| 5. How can I prepare effectively for a mathematics exam? |  |






















