Doc- Review: Sequence & Series of complex numbers | Topic-wise Tests & Solved Examples for Mathematics PDF Download
Review
Sequence & Series of complex numbers
First consider the useful facts
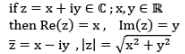

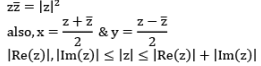
The △ in-equality : If z1 & z2 are arbitrary complex no., then
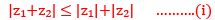
Proof: 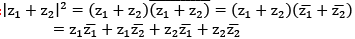
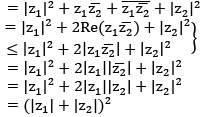
Taking positive sq. root yields the desired inequality.
Note: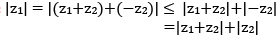
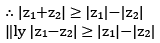
Note equality occur in (i)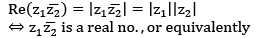
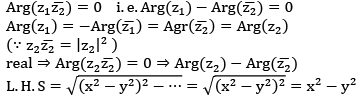
Note
Defn A seq. {zn} of complex no. is said to converge to a complex no. z if the seq. {|zn- z|} of real no. converge to 0
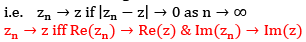
Proof forward Part :
Assume that zn → z then |zn- z|→ 0
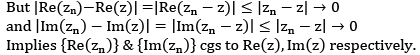
Converse Part : Assume that Re(zn) → Re(z) & Im(zn) → Im(z)
consider,
|zn - z|= |(xn + iyn )- (x+ iy)| where, zn = xn + iyn & z = x + iy
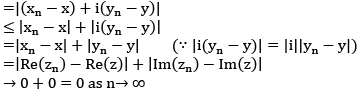
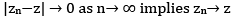
Note: {zn} can’t converge to more than one limit.
If exists is unique.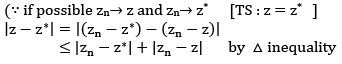
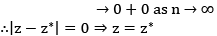
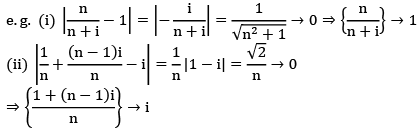
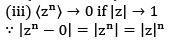
→ 0 as n→∞ (∵0 ≤|z|≤ 1)
Defn A seq. {zn} of complex no. is called a Cauchy seq. if for each 𝜖 > 0, there exists (N=N(𝜖)) an integer N s.t.
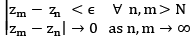
Cauchy Criteria for convergence in complex plane {zn} converges iff {zn} is a Cauchy seq.
Forward part: Assume that zn → z then
Re(zn) → Re(z) & Im(zn) → Im(z)
Proved before
Here {Re(zn)} & {Im(zn)} both are Cauchy seq. being convergent seq. of real no.
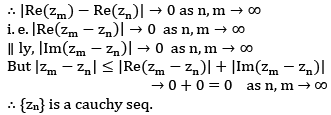
Converse part: suppose {zm} is a Cauchy seq. , then using
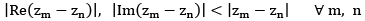
implies both {Re(zn) & Im(zn)} are cauchy seq. of real no. hence both converges,
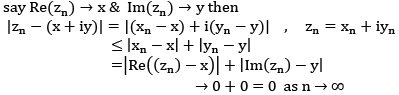
implies {zn} converges
Defn The infinite series 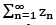 of complex nos. is said to be converge if the seq. {Sn},
of complex nos. is said to be converge if the seq. {Sn},
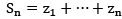 of paritial sum S is convergent.
of paritial sum S is convergent.
from the Cauchy criterion, i.e. “a seq. is conv. iff it is a Cauchy seq”, we see that 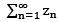 converges iff {Sn}is a cauchy seq.
converges iff {Sn}is a cauchy seq.
For each 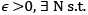
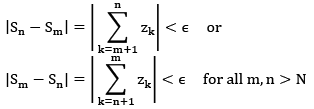
from this 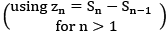 it follows that convergence of
it follows that convergence of 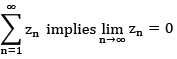 (i. e. a neccessary cond for the series
(i. e. a neccessary cond for the series 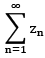 to converge is that zn →0 as n→ ∞
to converge is that zn →0 as n→ ∞
Remark's in the case of sequence we have,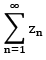 converges to z iff
converges to z iff
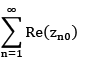
converges to Re(z) 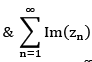 converge to Im(z).
converge to Im(z).
A sufficient condn for cgces of 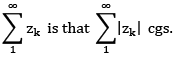
i.e. absolutely convergent series is cgt.
also, as with real series, we say a series 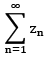 is said to be absolutely convergent if the series
is said to be absolutely convergent if the series 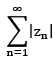 +ve real no. is convergent. Futher using the fact that
+ve real no. is convergent. Futher using the fact that
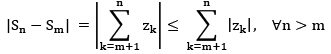
Implies that “every absolutely convergent series is convergent.” Converse is not true e.g.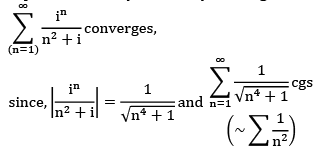
 absolutely and hence cgt.
absolutely and hence cgt.
Generalized Cauchy’s nth root test: let 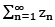 be a series of complex term such that
be a series of complex term such that
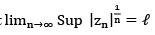
(a) if ℓ < 1 then series 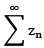 cgs abs.
cgs abs.
(b) if ℓ >1 then series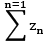 div.
div.
(c) if ℓ = 1 the series may or may not conv.
Generalised D’ lembert Ratio test: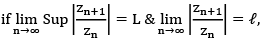 then
then
(a) if L < 1, then the series cgs absolutely
(b) if l > 1, the series div.
(c)if l≤1≤ L, no conclusion.
complex analysis ( Bak & Newmann)
Topology of the complex plane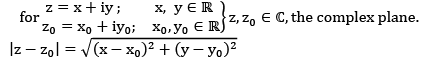
1.5 Definition
(i)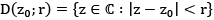 is called an open disc of radius r centered at z0 , also called nbhd of z0.
is called an open disc of radius r centered at z0 , also called nbhd of z0.
(ii) circle 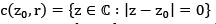
= circle with center z0 , radius r.
(iii) subset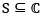 is called
is called 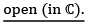 If for every
If for every 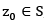 , there exists r > 0 . It means that some disc arround z lies entirely in S. for instance, the interior of a circle
, there exists r > 0 . It means that some disc arround z lies entirely in S. for instance, the interior of a circle 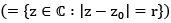 the entire complex plane
the entire complex plane 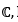 half plane (Re(z) , Im(z) <0 , Re(z) ) ect. are open sets. An open disc is an open set.
half plane (Re(z) , Im(z) <0 , Re(z) ) ect. are open sets. An open disc is an open set.
(iv) A set 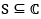 is s. t. b open iff for each
is s. t. b open iff for each 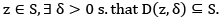
Note: 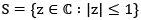 is not open
is not open
Note: 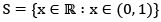 is open in
is open in 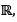 but not in
but not in 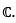
(v) set S is called closed if its complement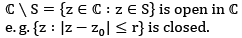
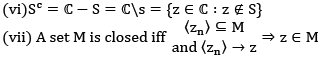
= Coll of points whose neighbourhood have a non empty intersection with both S and 
(ix) 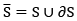 = closure of S
= closure of S
(x) S is bdry iff 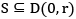 for some r > 0.
for some r > 0.
(xi) S is compact iff S is closed bdd 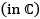
(xii) set S is said to be disconneced if there exists two disjoint open set s. t.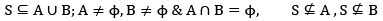
(xiii) S is s. t. b. disconnected iff S is a union of two non empty disjoit open subsets.
(xiv) S is called connected if it is not disconnected. in other words, S is connected if and only if, each pair of points z1, z1 of S can be connected by an arc lying in S
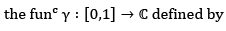
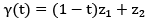 is calle the line segment with and points z1 & z2 and denoted by [z1,z2]
is calle the line segment with and points z1 & z2 and denoted by [z1,z2]
∴ if 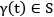 for each
for each 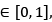 then the line segment [z1, z2] , (where z1 , z2 ∈S ) is said to be containe in S.
then the line segment [z1, z2] , (where z1 , z2 ∈S ) is said to be containe in S.
→ by a polygonal line from z1 to zn … . a finite union of line segments of the form 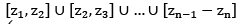
(z1 and zn are said to be polygonally connected)
→ A set S is said to be polygonally connected if any two points of S can be connected by a polygonal line (basically horizonal or verticaly) contained in S.
|
27 docs|150 tests
|
FAQs on Doc- Review: Sequence & Series of complex numbers - Topic-wise Tests & Solved Examples for Mathematics
| 1. What is a sequence of complex numbers? |  |
| 2. How is the nth term of a sequence of complex numbers determined? |  |
| 3. What is a series of complex numbers? |  |
| 4. How can we determine the sum of an infinite series of complex numbers? |  |
| 5. Can a sequence or series of complex numbers be divergent? |  |






















