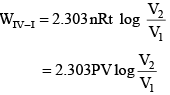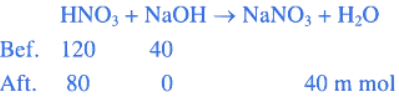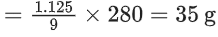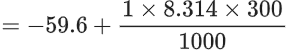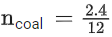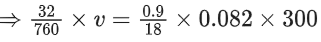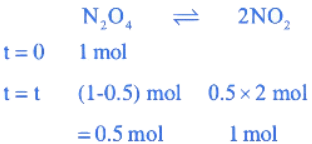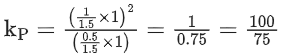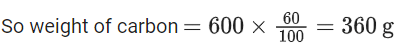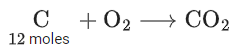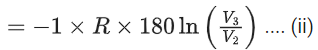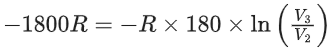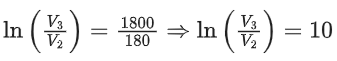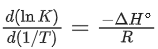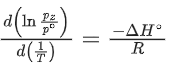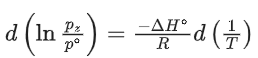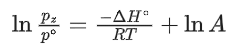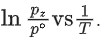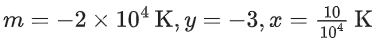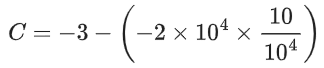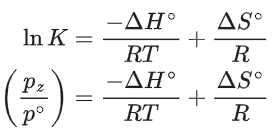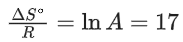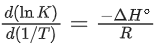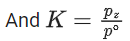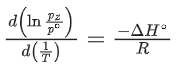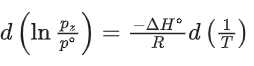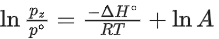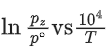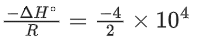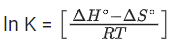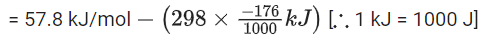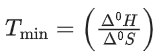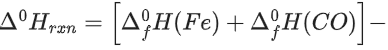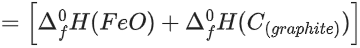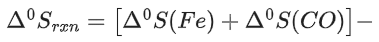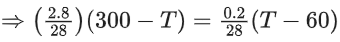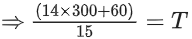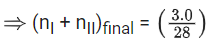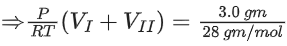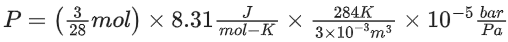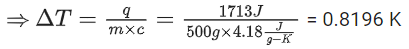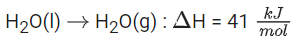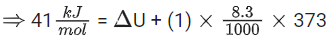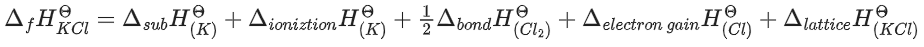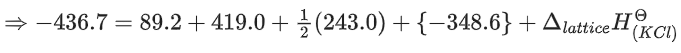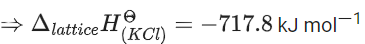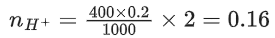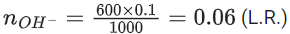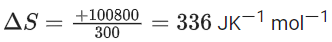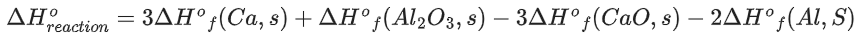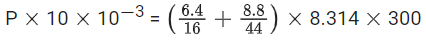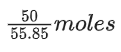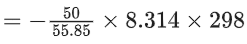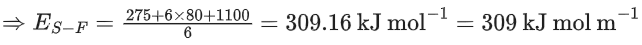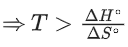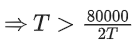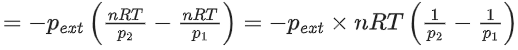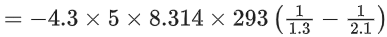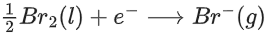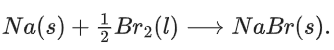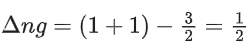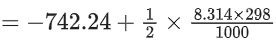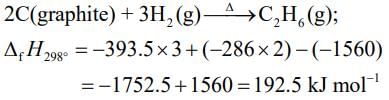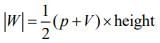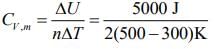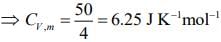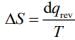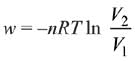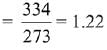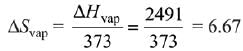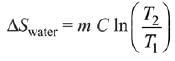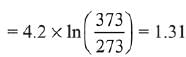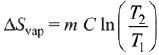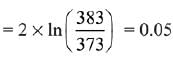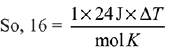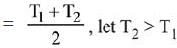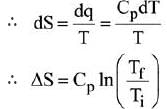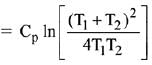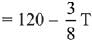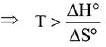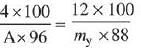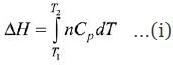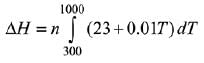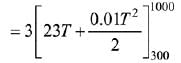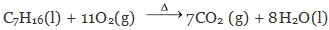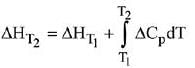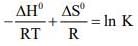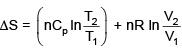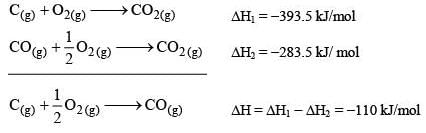JEE Main Previous Year Questions (2016- 2025): Thermodynamics PDF Download

Q.1. For independent processes at 300 K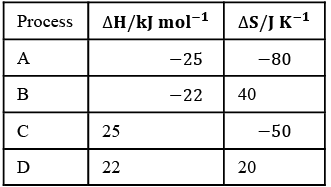

The number of non-spontaneous processes from the following is           (JEE Main 2023)

Ans. 2
For process A
ΔG = -25×10³-300(-80)
= –25000+24000
= –1000 ⇒ ΔG<0 spontaneous
For process B
ΔG = -22×10³-300(40)
= –22000–12000 ⇒ ΔG<0 spontaneous
For process C
ΔG = 25×10³-300 (-50)
= 25000+15000=40000 J
ΔG>0 ⇒ Non-spontaneous
For process D
ΔG = 22×10³-300(20)
ΔG>0 ⇒ Non-spontaneous.

Q.2. One mole of an ideal monoatomic gas is subjected to changes as shown in the graph. The magnitude of the work done (by the system or on the system) is_________ J (nearest integer)          (JEE Main 2023)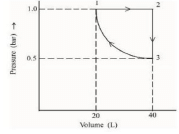

Ans. 6
I→II → Isobaric
II → III → Isochoric
III → I → Isothermal

W_I–II = 0

= 2.303(1x 20) log 2
= 2.303 x 20 x0.3010 = 13.818
W total = – 20 + 13.818 =  (– 6.182 lit alm) = 6.182 lit alm

Q.3. 2 mol of Hg(g) is combusted in a fixed volume bomb calorimeter with excess of O₂ at 298 K and 1 atm into HgO(s). During the reaction, temperature increases from 298.0 K to 312.8 K. If heat capacity of the bomb calorimeter and enthalpy of formation of Hg(g) are 20.00 kJ K⁻¹ and 61.32 kJ mol⁻¹ at 298 K, respectively, the calculated standard molar enthalpy of formation of HgO(s) at 298 K is XkJmol⁻¹. The value of |X| is _________ .

[Given: Gas constant R = 8.3 J K⁻¹ mol⁻¹]           (JEE Advanced 2022)

Ans. Between 89.00 and 91.00

Q.4. The correct option(s) about entropy (S) is(are)
[R= gas constant, F= Faraday constant, T= Temperature]          (JEE Advanced 2022)
(a) For the reaction, M(s) + 2H⁺(aq) → H₂(g) + M²⁺(aq), if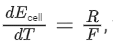then the entropy change of the reaction is R (assume that entropy and internal energy changes are temperature independent).
(b) The cell reaction, Pt(s)∣H₂(g, 1 bar )|H⁺(aq, 0.01M)‖H⁺(aq, 0.1M)|H²(g, 1bar)∣Pt(s), is an entropy driven process.
(c) For racemization of an optically active compound, ΔS > 0.
(d) ΔS > 0, for [Ni(H₂O)₆]²⁺ + 3 en → [Ni(en)₃]²⁺ + 6H₂O (where en = ethylenediamine).

Ans. b, c, d

Q.5. When 600 mL of 0.2 M HNO₃ is mixed with 400 mL of 0.1 M NaOH solution in a flask, the rise in temperature of the flask is ___________ × 10^−2∘C.

(Enthalpy of neutralisation = 57 kJ mol⁻¹ and Specific heat of water = 4.2JK⁻¹ g⁻¹) (Neglect heat capacity of flask)          (JEE Main 2022)

Ans. 54
HNO₃
600 mL × 0.2 M = 120 m mol
NaOH
400 mL × 0.1 M = 40 m mol 

Heat liberated from reaction
= 40 × 10⁻³ × 57 × 10³ J
Heat gained by solution = mCΔT
m = mass of solution = V × d = 1000 × 1 = 1000 g
Heat gained by solution = 1000 × 4.2 × ΔT…(2)
From (1) and (2)
Heat liberated = Heat gained
40 × 10⁻³ × 57 × 10³ = 1000 × 4.2 × ΔT
ΔT = 54 × 10^−2∘C
(Rounded off to the nearest integer) 

Q.6. Among the following the number of state variables is __________.
Internal energy (U)
Volume (V)
Heat (q)
Enthalpy (H)          (JEE Main 2022)

Ans. 3
State variables are internal energy (U), Volume (V) and Enthalpy (H). 

Q.7. A gas (Molar mass = 280  g mol⁻¹) was burnt in excess O₂ in a constant volume calorimeter and during combustion the temperature of calorimeter increased from 298.0 K to 298.45 K. If the heat capacity of calorimeter is 2.5 kJ K⁻¹ and enthalpy of combustion of gas is 9 kJ mol⁻¹ then amount of gas burnt is _____________ g. (Nearest Integer)           (JEE Main 2022)

Ans. 35
ΔU = CΔT
= 2.5 × 10³ × 0.45 = 1.125 kJ
Considering ΔH ≃ ΔU
ΔH = 9 kJ/mol ≃ ΔU
∴ Mass of gas burnt

Q.8. For the reaction
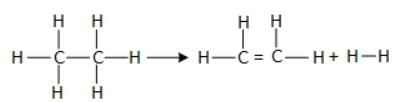
H₂F₂( g) → H₂(g) + F₂(g)
ΔU = −59.6 kJ mol⁻¹ at 27^∘C.
The enthalpy change for the above reaction is (−) __________ kJmol⁻¹ [nearest integer]
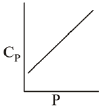
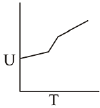
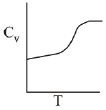
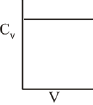
Given: R = 8.314 J K⁻¹ mol⁻¹.           (JEE Main 2022)

Ans. 57
H₂F₂( g) ⟶ H₂(g) + F₂(g)
ΔU = −59.6 kJ mol⁻¹ at 27^∘C
ΔH = ΔU + Δn_gRT

=−57.10 kJ mol⁻¹

Q.9. 2.4 g coal is burnt in a bomb calorimeter in excess of oxygen at 298 K and 1 atm pressure. The temperature of the calorimeter rises from 298 K to 300 K. The enthalpy change during the combustion of coal is −x kJ mol⁻¹. The value of x is ___________. (Nearest Integer)
(Given: Heat capacity of bomb calorimeter 20.0 kJ K⁻¹. Assume coal to be pure carbon)           (JEE Main 2022)

Ans. 200



Q = −200 kJ/mol
x = 200

Q.10. While performing a thermodynamics experiment, a student made the following observations.
HCl + NaOH → NaCl + H₂O ΔH = −57.3 kJ mol⁻¹
CH₃COOH + NaOH → CH₃COONa + H₂O ΔH = −55.3 kJ mol⁻¹
The enthalpy of ionization of CH₃COOH as calculated by the student is _____________ kJ mol⁻¹. (nearest integer)           (JEE Main 2022)

Ans. 2
(I) HCl + NaOH → NaCl + H₂O
ΔH₁ = −57.3KJmol⁻¹ 
(II) CH₃COOH + NaOH → CH₃COONa + H₂O
ΔH₂ = −55.3KJmol⁻¹
Reaction (I) can be written as
(III) NaCl + H₂O → HCl + NaOH
ΔH₃ = 57.3KJmol⁻¹ 
By adding (II) and (III)
CH₃COOH + NaCl → CH₃COONa + HCl ΔHr
ΔH_r = ΔH₃ + ΔH₂ = 57.3 − 55.3
= 2 kJ mol⁻¹

Q.11. 2.2 g of nitrous oxide (N₂O) gas is cooled at a constant pressure of 1 atm from 310 K to 270 K causing the compression of the gas from 217.1 mL to 167.75 mL. The change in internal energy of the process, ΔU is '−x' J. The value of 'x' is ________. [nearest integer]
(Given: atomic mass of N = 14 g mol⁻¹ and of O = 16 g mol⁻¹. Molar heat capacity of N₂O is 100 J K⁻¹ mol⁻¹)          (JEE Main 2022)

Ans. 195

Q.12. A box contains 0.90 g of liquid water in equilibrium with water vapour at 27^∘C. The equilibrium vapour pressure of water at 27^∘C is 32.0 Torr. When the volume of the box is increased, some of the liquid water evaporates to maintain the equilibrium pressure. If all the liquid water evaporates, then the volume of the box must be __________ litre. [nearest integer]

(Given: R = 0.082 L atm K⁻¹ mol⁻¹)
(Ignore the volume of the liquid water and assume water vapours behave as an ideal gas.)          (JEE Main 2022)

Ans. 29
We know, 760 Torr = 1 atm
∴ 32 Torr = 32/760 atm
As all the liquid water evaporates so entire water is in gaseous state.
∴ Weight of water vapour = 0.9 g
∴ Moles of water vapour (n) = 0.9/18
Pressure (P) = 32/760 atm
Temperature (T) = (27 + 273) K = 300 K
R = 0.082 L atm K⁻¹ mol⁻¹
Given water vapour act as an ideal gas, so we can apply ideal gas equation.
From ideal gas equation,
PV = nRT

⇒ v = 29 L

Q.13. 17.0 g of NH₃ completely vapourises at −33.42^∘C and 1 bar pressure and the enthalpy change in the process is 23.4 kJ mol⁻¹. The enthalpy change for the vapourisation of 85 g of NH₃ under the same conditions is _________ kJ.           (JEE Main 2022)

Ans. 117

Q.14. For combustion of one mole of magnesium in an open container at 300 K and 1 bar pressure, Δ_CH^Θ = −601.70 kJ mol⁻¹, the magnitude of change in internal energy for the reaction is __________ kJ. (Nearest integer)
(Given: R = 8.3 J K⁻¹ mol⁻¹)         (JEE Main 2022)

Ans. 600

Q.15. 4.0 L of an ideal gas is allowed to expand isothermally into vacuum until the total volume is 2.0 L. The amount of heat absorbed in this expansion is ____________ L atm.        (JEE Main 2022)

Ans. 0 

Q.16. When 5 moles of He gas expand isothermally and reversibly at 300 K from 10 litre to 20 litre, the magnitude of the maximum work obtained is __________ J. [nearest integer] 
(Given: R = 8.3 J K⁻¹ mol⁻¹ and log 2 = 0.3010)         (JEE Main 2022)

Ans. 8630

Q.17. A fish swimming in water body when taken out from the water body is covered with a film of water of weight 36 g. When it is subjected to cooking at 100∘C, then the internal energy for vaporization in kJ mol⁻¹ is ___________. [nearest integer]
[Assume steam to be an ideal gas. Given Δ_vapHΘ for water at 373 K and 1 bar is 41.1 kJ mol⁻¹ ; R = 8.31 J K⁻¹ mol⁻¹]         (JEE Main 2022)

Ans. 38

Q.18. 2.0 g of H₂ gas is adsorbed on 2.5 g of platinum powder at 300 K and 1 bar pressure. The volume of the gas adsorbed per gram of the adsorbent is __________ mL.
(Given: R = 0.083 L bar K⁻¹ mol⁻¹)        (JEE Main 2022)

Ans. 9960

Q.19. For complete combustion of methanol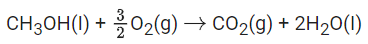 

the amount of heat produced as measured by bomb calorimeter is 726 kJ mol⁻¹ at 27∘C. The enthalpy of combustion for the reaction is −x kJ mol⁻¹, where x is ___________. (Nearest integer)
(Given: R = 8.3 JK⁻¹ mol⁻¹)        (JEE Main 2022)

Ans. 727

Q.20. The standard free energy change (ΔG^∘) for 50% dissociation of N₂O₄ into NO₂ at 27^∘C and 1 atm pressure is − x J mol⁻¹. The value of x is ___________. (Nearest Integer)
[Given: R = 8.31 J K⁻¹ mol⁻¹, log 1.33 = 0.1239 ln 10 = 2.3]        (JEE Main 2022)

Ans. 720


= 1.33 
ΔG° = −RTℓnkP 
= −8.31 × 300 × ln⁡(1.33)
= −710.45 J/mol

Q.21. The standard entropy change for the reaction
4Fe(s) + 3O₂(g) → 2Fe₂O₃(s) is −550 J K⁻¹ at 298 K.
[Given: The standard enthalpy change for the reaction is −165 kJ mol⁻¹]. The temperature in K at which the reaction attains equilibrium is _____________. (Nearest Integer)        (JEE Main 2022)

Ans. 300
ΔG = ΔH − TΔS = 0 at equilibrium
⇒ −165 × 10³ − T × (−505) = 0
⇒ T = 300 K

Q.22.  C(s) + O₂(g) → CO₂(g) + 400 kJ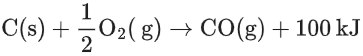

When coal of purity 60% is allowed to burn in presence of insufficient oxygen, 60% of carbon is converted into 'CO' and the remaining is converted into 'CO₂'. The heat generated when 0.6 kg of coal is burnt is _________.        (JEE Main 2022)
(a) 1600 kJ 
(b) 3200 kJ 
(c) 4400 kJ 
(d) 6600 kJ

Ans. d
Weight of coal = 0.6 kg = 600gm
∴ 60% of it is carbon 

∴ moles of carbon = 360/12 = 30 moles

∴ Heat generated = 12 × 400 + 18 × 100 = 6600 kJ

Q.23. Given below are two statements: One is labelled as Assertion A and the other is labelled as Reason R
Assertion A: The reduction of a metal oxide is easier if the metal formed is in liquid state than solid state.
Reason R: The value of ΔGΘ becomes more on negative side as entropy is higher in liquid state than solid state.
In the light of the above statements, choose the most appropriate answer from the options given below:         (JEE Main 2022)
(a) Both A and R are correct and R is the correct explanation of A
(b) Both A and R are correct but R is NOT the correct explanation of A
(c) A is correct but R is not correct
(d) A is not correct but R is correct

Ans. a
Reduction of a metal oxide is easier if the metal is formed in a liquid state at the temperature of reduction because the entropy is higher if the metal is in a liquid state.

Q.24. Which of the following relation is not correct?         (JEE Main 2022)
(a) ΔH = ΔU − PΔV
(b) ΔU = q + W
(c) ΔS_sys  + ΔS_surr ⩾ 0
(d) ΔG = ΔH − TΔS

Ans. a
If U + Pv (By definition)
Δ14 = ΔU + Δ(Pr) at constant pressure
ΔH = ΔU + PΔV

Q.25. For micelle formation, which of the following statements are correct?
A. Micelle formation is an exothermic process.
B. Micelle formation is an endothermic process.
C. The entropy change is positive.
D. The entropy change is negative.         (JEE Main 2022)
(a) A and D only
(b) A and C only
(c) B and C only
(d) B and D only

Ans. a
Micelle formation is an endothermic process with positive entropy change. 

Q.26. Match List-I with List-II.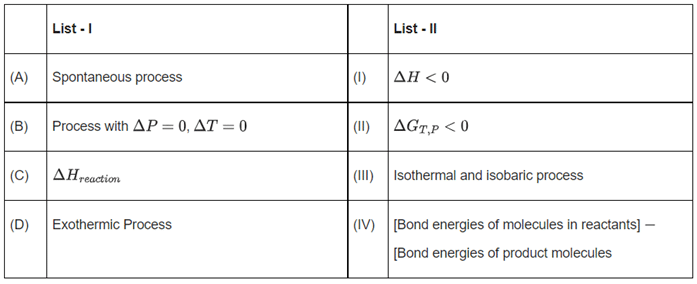
Choose the correct answer from the options given below:         (JEE Main 2022)
(a) (A) - (III), (B) - (II), (C) - (IV), (D) - (I)
(b) (A) - (II), (B) - (III), (C) - (IV), (D) - (I)
(c) (A) - (II), (B) - (III), (C) - (I), (D) - (IV)
(d) (A) - (II), (B) - (I), (C) - (III), (D) - (IV)

Ans. b
(A) For a spontaneous process ΔG_T,P < 0
(B) ΔP = 0 → Isobaric process, ΔT = 0 → Isothermal process
(C) ΔH_reaction = (Σ Bond energies of reactants) - (Σ bond energies of products)
(D) ΔH < 0 is for exothermic reaction 

Q.27. At 25^∘C and 1 atm pressure, the enthalpy of combustion of benzene (I) and acetylene (g) are − 3268 kJ mol⁻¹ and −1300 kJ mol⁻¹, respectively. The change in enthalpy for the reaction 3 C₂H₂(g) → C₆H₆ (I), is         (JEE Main 2022)
(a) + 324 kJ mol⁻¹ 
(b) + 632 kJ mol⁻¹ 
(c) − 632 kJ mol⁻¹ 
(d) − 732 kJ mol⁻¹

Ans. c

Q.28. At 25^∘C and 1 atm pressure, the enthalpies of combustion are as given below: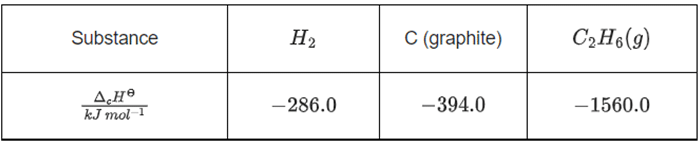 
The enthalpy of formation of ethane is        (JEE Main 2022)
(a) +54.0 kJ mol⁻¹
(b) −68.0 kJ mol⁻¹
(c) −86.0 kJ mol⁻¹
(d) +97.0 kJ mol⁻¹

Ans. c
2C (graphite) + 3H₂(g) → C₂H₆(g)
ΔH_r = +1560 + 2(−394) + 3(−286)
= −86.0 kJ mol⁻¹
Enthalpy of formation of C₂H₆(g) = –86.0 kJ mol^–1 

Q.29. One mole of an ideal gas at 900 K, undergoes two reversible processes, I followed by II, as shown below. If the work done by the gas in the two processes are same, the value of ln ⁡V₃ / V₂ is _________.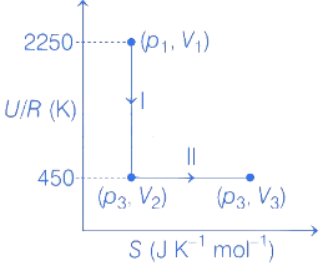 
(U : internal energy, S : entropy, p : pressure, V : volume, R : gas constant)
(Given: molar heat capacity at constant volume, C_V,m of the gas is 5/2R)      (JEE Advanced 2021)

Ans. 10
For process 1, entropy is constant thus, q is constant
∴ WI = ΔU = nC_V,_mΔT
= −(2250 − 450)R = −1800R .... (i)
ΔU = nC_V,mΔT
−1800R = 1 × 5R/2 × ΔT
⇒ ΔT = −720K
T₂ − T₁ = −720K
T2 = −720K + 900K = 180K
For process II,


As, both work done for process I and II are equal,
Therefore, W_I = W_II

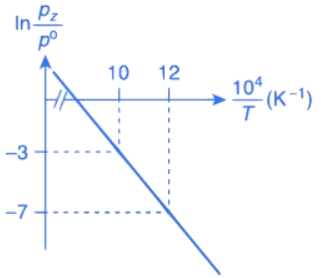
Q.30. For the reaction, X(s) ⇌ Y(s) + Z(g), the plot of ln ⁡p^z/p^θ versus 10⁴/T is given below (in solid line), where p_z is the pressure (in bar) of the gas Z at temperature T and p^θ = 1 bar.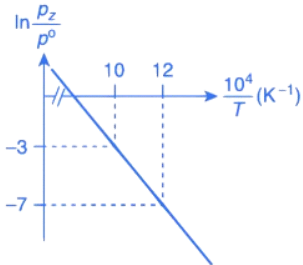 
(Given, 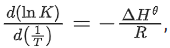where the equilibrium constant, K = p^z/p^θ and the gas constant, R = 8.314 J K⁻¹ mol⁻¹)
The value of ΔS^θ (in J K⁻¹ mol⁻¹) for the given reaction, at 1000 K is _________.     (JEE Advanced 2021)

Ans. 141.34
For the given reaction,
X(s) ⇌ X(s) + Z(g)
We have

And K = p^z/p^∘
Substituting the value of K in Eq. (1), we get

Or

Integrating both sides of Eq. (2), we get

Where ln⁡ A = Integration constant
We can also calculate the intercept (ln⁡A) from the plot of
Now, from the equation of straight line, we have
or
y = mx + C
C = y − mx
From the plot, we have

Now, substituting the above values in Eq. (4), we get

= −3 + 20C
= 17
⇒ C = 17
This intercept is equal to ln⁡ A in Eq. (3), so we have
ln⁡ A = C = 17
From the thermodynamic equations, we have
ΔG^∘ = ΔH^∘ − 7ΔS^∘
For any equilibrium reaction, the Gibb's energy is,
ΔG^∘ = −RT ln⁡ K
On comparing both the equations, we get
−RT ln⁡ K = ΔH^∘ − TΔS^∘
Or

On comparing Eq. (3) and (6), we have

Or
ΔS^∘ = 17R
= 17 × 8.314
= 141.34JK⁻¹

Q.31. For the reaction, X(s) ⇌ Y(s) + Z(g), the plot of ln ⁡p^z/p^θ versus 10⁴/T is given below (in solid line), where pz is the pressure (in bar) of the gas Z at temperature T and pθ = 1 bar.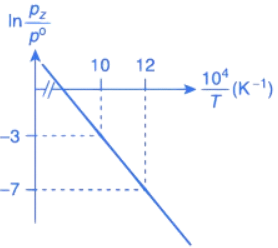

(Given,where the equilibrium  constant, K = p^z/p^θ and the gas constant, R = 8.314 J K⁻¹ mol⁻¹)
The value of standard enthalpy, ΔHo (in kJ mol−1) for the given reaction is _______.     (JEE Advanced 2021)

Ans. 166.28
For the given reaction,
X(s) ⇌ X(s) + Z(g)
We have


Substituting the value of K in Eq. (1), we get

Or

Integrating both sides of Eq. (2), we get

Where ln⁡ A = Integration constant
From the given plot of

The slope of the plot is


ΔH^∘ = −2 × 10⁴ × R
ΔH^∘ = 2 × 8.314 × 10⁴ 
ΔH^∘ = 16.628 × 10⁴ J mol⁻¹ 
ΔH^∘ = 166.28 kJ mol⁻¹

Q.32. An ideal gas undergoes a reversible isothermal expansion from state I to state II followed by a reversible adiabatic expansion from state II to state III. The correct plot(s) representing the changes from state I to state III is (are)
(p : pressure, V : volume, T : temperature, H : enthalpy, S : entropy)     (JEE Advanced 2021) 

(a)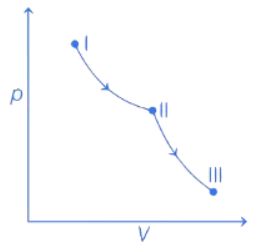
(b)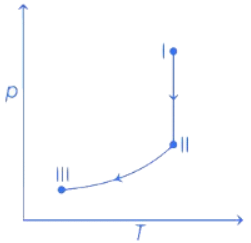
(c)
(d)

Ans. d
From state I to II Reversible isothermal expansion takes place. So, following changes take place,

• pressure decreases.
• Volume increases.
• Temperature remains constant.
• Enthalpy, H remains constant.
• Entropy, S for expansion increases.

So, all options follows the above mentioned conditions, so all graphs are correct for state I and II.

From state II to III Reversible adiabatic expansion takes place. So, following changes take place.

• pressure decreases.
• Volume increases.
• Temperature decreases.
• Enthalpy, H decreases.
• Entropy, S remains constant.
• H increases instead of decreasing, so only option (c) is incorrect.

All other options, i.e., (a), (b) and (d) follows the above mentioned conditions.
Therefore, correct graphical representations are (a), (b) and (d).

Q.33. The incorrect expression among the following is:     (JEE Main 2021)
(a)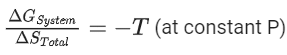

(b)
(c)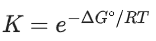

(d) For isothermal process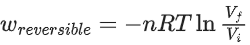

Ans. b
Option (b) is incorrect.
ΔG^∘ = −RT ln K
ΔH^∘ − TΔS^∘ = −RT ln K 

Q.34. During which of the following processes, does entropy decrease?
(A) Freezing of water to ice at 0^∘C
(B) Freezing of water to ice at −10^∘C
(C) N₂(g) + 3H₂(g) → 2NH₃(g)
(D) Adsorption of CO(g) on lead surface
(E) Dissolution of NaCl in water
Choose the correct answer from the options given below:    (JEE Main 2021)
(a) (A), (C) and (E) only
(b) (B) and (C) only 
(c) (A), (B), (C) and (D) only 
(d) (A) and (E) only

Ans. c
A, B → Freezing of water will decrease entropy as particles will move closer and forces of attraction will increase. This leads to decrease in randomness. So entropy decrease.
C → No. of molecules decreasing
D → Adsorption will lead to decrease in randomness of gaseous particles.
E → NaCl(s) → Na⁺(aq) + Cl^–(aq) ΔS > 0
So, (A, B, C, D) decreases entropy. 

Q.35. For the reaction, 2NO₂(g) ⇌ N₂O₄(g), when ΔS = −176.0 JK⁻¹ and ΔH = −57.8 kJ mol⁻¹, the magnitude of ΔG at 298 K for the reaction is ___________ kJ mol⁻¹. (Nearest integer)     (JEE Main 2021)

Ans. 5
Given, ΔH = − 57.8 kJ mol⁻¹
ΔS = − 176 JK⁻¹ mol⁻¹
T = 298 K
Using Gibb's free energy relation
ΔG = ΔH − TΔS
where, ΔG = change in Gibb's free energy
ΔH = change in enthalpy
T = temperature
ΔS = change in entropy
ΔG = 57.8 kJ/mol − [298 K × (− 176 Jk⁻¹ mol⁻¹)]

= − 5.352 kJ/mol
| ΔG | = 5.352
Hence, answer is 5.

Q.36. Data given for the following reaction is as follows:
FeO_(s) + C_(graphite) → Fe_(s) + CO_(g) 

The minimum temperature in K at which the reaction becomes spontaneous is ___________. (Integer answer)      (JEE Main 2021)

Ans. 964



= [0 − 110.5] − [−266.3 + 0] = 155.8 kJ/mol


= [27.28 + 197.6] − [57.49 + 5.74] 
= 161.65 J/mol-K

≃ 964 k (nearest integer)

Q.37. Two flasks I and II shown below are connected by a valve of negligible volume.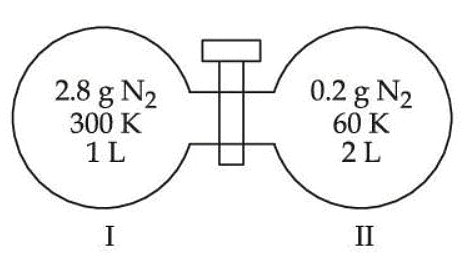 
When the valve is opened, the final pressure of the system in bar is x × 10⁻². The value of x is __________. (Integer answer)
[Assume - Ideal gas; 1 bar = 10⁵ Pa; Molar mass of N₂ = 28.0 g mol⁻¹; R = 8.31 J mol⁻¹ K⁻¹]       (JEE Main 2021)

Ans. 84
Applying; (n_I + n_II)_initial = (n_I + n_II)_final
⇒ Assuming the system attains a final temperature of T (such that 300 < T < 60) 

⇒ n₁C_m(300 − T) = n_IIC_m(T − 60) 

⇒ 14(300 − T) = T − 60 

⇒ T = 284 K (final temperature)
⇒ If the final pressure = P 



⇒ 0.84287 bar
⇒ 84.28 × 10⁻² bar
⇒ 84 

Q.38. 200 mL of 0.2 M HCl is mixed with 300 mL of 0.1 M NaOH. The molar heat of neutralization of this reaction is −57.1 kJ. The increase in temperature in ^∘C of the system on mixing is x × 10⁻². The value of x is ___________. (Nearest integer)
[Given: Specific heat of water = 4.18 J g⁻¹ K⁻¹, Density of water = 1.00 g cm⁻³]
[Assume no volume change on mixing)        (JEE Main 2021)

Ans. 82
⇒ Millimoles of HCl = 200 × 0.2 = 40
⇒ Millimoles of NaOH = 300 × 0.1 = 30 
⇒ Heat released = (30/1000 × 57.1 × 1000) = 1713 J
⇒ Mass of solution = 500 ml × 1 gm/ml = 500 gm 

= 81.96 × 10⁻² K

Q.39. For water Δ_vap H = 41 kJ mol⁻¹ at 373 K and 1 bar pressure. Assuming that water vapour is an ideal gas that occupies a much larger volume than liquid water, the internal energy change during evaporation of water is ___________ kJ mol⁻¹
[Use: R = 8.3 J mol⁻¹ K⁻¹]         (JEE Main 2021)

Ans. 38

⇒ From the relation : ΔH = ΔU + Δn_gRT 

Δ DU = 41 − 3.0959 = 38 kJ/mol

Q.40. The Born-Haber cycle for KCl is evaluated with the following data:
Δ_fH^Θ for KCl = −436.7 kJ mol⁻¹ ;
Δ_subH^Θ for K = 89.2 kJ mol⁻¹ ;
Δ_ionizationH^Θ for K = 419.0 kJ mol⁻¹ ;
Δ_electrongainH^Θ for Cl_(g) = −348.6 kJ mol⁻¹ ;
Δ_bondH^Θ for Cl₂ = 243.0 kJ mol⁻¹
The magnitude of lattice enthalpy of KCl in kJ mol⁻¹ is _____________ (Nearest integer)         (JEE Main 2021)

Ans. 718



The magnitude of lattice enthalpy of KCl in kJ mol⁻¹ is 718 (Nearest integer). 

Q.41. When 400 mL of 0.2 M H₂SO₄ solution is mixed with 600 mL of 0.1 M NaOH solution, the increase in temperature of the final solution is __________ × 10⁻² K. (Round off to the nearest integer).
[Use : H⁺ (aq) + OH⁻ (aq) → H₂O : Δ_γH = −57.1 kJ mol⁻¹]
Specific heat of H₂O = 4.18 J K⁻¹ g⁻¹
density of H₂O = 1.0 g cm⁻³
Assume no change in volume of solution on mixing.          (JEE Main 2021)

Ans. 82


Now, heat liberated from reaction = heat gained by solutions
or, 0.06 × 57.1 × 10³
= (1000 × 1.0) × 4.18 × ΔT
∴ ΔT = 0.8196K
= 81.96 × 10⁻² K ≈ 82 × 10⁻² K

Q.42. For water at 100^∘ C and 1 bar,
Δ_vap H − Δ_vap U = _____________ × 10² J mol⁻¹. (Round off to the Nearest Integer)
[Use : R = 8.31 J mol⁻¹ K⁻¹]
[Assume volume of H₂O(l) is much smaller than volume of H₂O(g). Assume H₂O(g) treated as an ideal gas]         (JEE Main 2021)

Ans. 31
H₂O_(l) ⇌ H₂O_(v)
ΔH = ΔU + Δn_gRT
For 1 mole waters;
Δn_g = 1
∴ Δn_gRT = 1 mol × 8.31 J/mol-k × 373 K
= 3099.63 J ≅ 31 × 10² J 

Q.43. A system does 200 J of work and at the same time absorbs 150 J of heat. The magnitude of the change in internal energy is ____________ J. (Nearest integer)          (JEE Main 2021)

Ans. 50
w = −200 J, q = +150 : ΔU = q + w
ΔU = 150 − 200 = −50 J
Magnitude = 50 J = |ΔU | 

Q.44. At 298 K, the enthalpy of fusion of a solid (X) is 2.8 kJ mol⁻¹ and the enthalpy of vaporisation of the liquid (X) is 98.2 kJ mol⁻¹. The enthalpy of sublimation of the substance (X) in kJ mol⁻¹ is _____________. (in nearest integer)           (JEE Main 2021)

Ans. 101
ΔH_sub = ΔH_fus. + ΔH_vap.
= 2.8 + 98.2
= 101 kJ/mol

Q.45. If the standard molar enthalpy change for combustion of graphite powder is −2.48 × 10² kJ mol⁻¹, the amount of heat generated on combustion of 1 g of graphite powder is ___________ kJ. (Nearest integer)           (JEE Main 2021)

Ans. 21
1 mol graphite = 12 gm C
For 1 g of graphite = 248/12 = 20.67 kJ/gm heat evolved.  

Q.46. For a given chemical reaction A → B at 300 K the free energy change is −49.4 kJ mol⁻¹ and the enthalpy of reaction is 51.4 kJ mol⁻¹. The entropy change of the reaction is _____________ JK⁻¹ mol⁻¹.            (JEE Main 2021)

Ans. 336
ΔG = −49.4 kJ/mol
ΔH = 51.4 kJ/mol
ΔG = ΔH − TΔS
−49400 = 51400 − 300ΔS 

Q.47. For the reaction C₂H₆ → C₂H₄ + H₂
the reaction enthalpy Δ_rH = __________ kJ mol⁻¹. (Round off to the Nearest Integer).
[Given: Bond enthalpies in kJ mol⁻¹ : C-C : 347, C = C : 611; C-H : 414, H-H : 436]             (JEE Main 2021)

Ans. 128

ΔH = E_C−C + 6E_C−H − E_C=C − 4E_C−H − E_H−H
= 347 + 6(414) − 611 − 4 × 414 − 436
= 347 + 828 − 1047
= 128 KJ/ mol 

Q.48. The standard enthalpies of formation of Al₂O₃ and CaO are −1675 kJ mol^-1 and −635 kJ mol⁻¹ respectively.
For the reaction
3CaO + 2Al → 3Ca + Al₂O₃ the standard reaction enthalpy Δ_rH⁰ = _________ kJ.
(Round off to the Nearest Integer)              (JEE Main 2021)

Ans. 230
3CaO + 2Al ⟶ 3Ca + Al₂O₃

= 0 + (−1675) − 3(−635) − 0
= −1675 + 1905
= 230 KJ

Q.49. The pressure exerted by a non-reactive gaseous mixture of 6.4g of methane and 8.8 g of carbon dioxide in a 10L vessel at 27^∘C is __________ kPa. (Round off to the Nearest Integer).
[Assume gases are ideal, R = 8.314 J mol⁻¹ K⁻¹
Atomic masses : C : 12.0 u, H : 1.0 u, O : 16.0 u]              (JEE Main 2021)

Ans. 150
V = 10 L, T = 27∘ C = 300 K
(m)_methane = 6.4 g, (m)_CO2 = 8.8 g
PV = n_totalRT

P × 10⁻² = (0.4 + 0.2) × 8.314 × 300
P = 149652 Pa
P = 149.652 KPa ≈ 150 kPa  

Q.50. At 25^∘C, 50 g of iron reacts with HCl to form FeCl₂. The evolved hydrogen gas expands against a constant pressure of 1 bar. The work done by the gas during this expansion is _________ J. (Round off to the Nearest Integer).
[Given: R = 8.314 J mol⁻¹ K⁻¹. Assume, hydrogen is an ideal gas] [Atomic mass of Fe is 55.85 u]              (JEE Main 2021)

Ans. 2218
Fe + 2HCl → FeCl₂ + H₂

Moles of Fe =  = Moles of H₂
No. of H₂ produced =
Work done = −P_ext . ΔV
= −Δn_gRT

= -2218.05 J
Nearest integer = 2218  

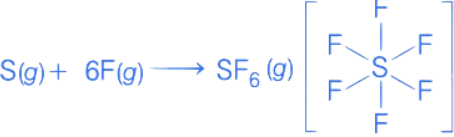
Q.51. The average S-F bond energy in kJ mol⁻¹ of SF₆ is __________. (Rounded off to the nearest integer)
[Given: The values of standard enthalpy of formation of SF₆(g), S(g) and F(g) are - 1100, 275 and 80 kJ mol⁻¹ respectively.]              (JEE Main 2021)

Ans. 309


So, Δ_fH^∘[S, g] + 6 × Δ_fH^∘[F, g] = Δ_fH^∘[SF₆, g] + 6 × E_S−F
[∴ E_S−F = Average S − F bond energy in SF₆]
275 + 6 × 80 = −1100 + 6 × E_S−F

Q.52. An exothermic reaction X → Y has an activation energy 30 kJ mol⁻¹. If energy change ΔE during the reaction is −20 kJ, then the activation energy for the reverse reaction in kJ is ___________. (Integer answer)               (JEE Main 2021)

Ans. 50
X → Y
ΔE = (E_a)_f – (E_a)_b
⇒ – 20 = 30 – (E_a)_b
⇒ (E_a)_b = 50 kJ 

Q.53. For a chemical reaction A + B ⇌ C + D
(Δ_rH^Θ = 80 kJ mol⁻¹) the entropy change Δ_rS^Θ depends on the temperature T (in K) as Δ_rS^Θ = 2T (J K⁻¹mol⁻¹).
Minimum temperature at which it will become spontaneous is ___________ K. (Integer)               (JEE Main 2021) 

Ans. 200
We know, ΔG^∘ = ΔH^∘ − TΔS^∘
For a reaction to be spontaneous
ΔG^∘ < 0
⇒ ΔH^∘ − TΔS^∘ < 0


⇒ 2T² > 80000
⇒ T² > 40000
⇒ T > 200
The minimum temperature to make it spontaneous is 200 K. 

Q.54. Five moles of an ideal gas at 293 K is expanded isothermally from an initial pressure of 2.1 MPa to 1.3 MPa against at constant external pressure 4.3 MPa. The heat transferred in this process is _________ kJ mol⁻¹. (Rounded off to the nearest integer) [Use R = 8.314 J mol⁻¹K⁻¹]               (JEE Main 2021) 

Ans. 15
The gas performs isothermal irreversible work (W).
where, ΔU = 0 (change in internal energy)
From, 1st law of thermodynamics,
⇒ ΔU = ΔQ + W
⇒ 0 = ΔQ + W
⇒ ΔQ = −W
Now, W = −p_ext(V₂ − V₁)

Given, p_ext = 4.3 MPa, p₁ = 2.1 MPa, p₂ = 1.3 MPa, n = 5 mol, T = 293 K and R = 8.314 J mol⁻¹ K⁻¹

= − 15347.70 J mol⁻¹

= − 15.347 kJ mol⁻¹ ≃ − 15 kJ mol⁻¹

⇒ ΔQ = 15 kJ mol⁻¹

Q.55. The ionization enthalpy of Na⁺ formation from Na_(g) is 495.8 kJ mol⁻¹, while the electron gain enthalpy of Br is −325.0 kJ mol⁻¹. Given the lattice enthalpy of NaBr is −728.4 kJ mol⁻¹. The energy for the formation of NaBr ionic solid is (−) ____________ × 10⁻¹ kJ mol⁻¹.               (JEE Main 2021)  

Ans. 5576
Na(s) ⟶ Na ⁺ (g)
ΔH = 495.8

ΔH = 325
Na⁺(g) + Br⁻(g) ⟶ NaBr(s)
ΔH = −728.4

ΔH = ?
ΔH = 495.8 − 325 − 728.4 − 557.6 kJ
= −5576 × 10⁻¹ kJ

 Q.56. The reaction of cyanamide, NH₂CN_(s) with oxygen was run in a bomb calorimeter and ΔU was found to be −742.24 kJ mol⁻¹. The magnitude of ΔH₂₉₈ for the reaction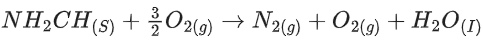

is _________ kJ. (Rounded off to the nearest integer) [Assume ideal gases and R = 8.314 J mol⁻¹ K⁻¹]              (JEE Main 2021)  

Ans. 741
 

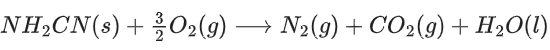
ΔH = ΔU + ΔngRT

= −742.24 + 1.24
= −741 kJ/mol 

Q.57. For the reaction
A(l) → 2B(g)

ΔU = 2.1 kcal, ΔS = 20 cal K⁻¹ at 300 K.
Hence ΔG in kcal is ______.    (2020)

Ans. -2.70

 For the reaction

A(l) → 2B(g)

Δn_g = 2 − 0 = 2

From the relation

ΔH = ΔU + Δn_gRT ...(1)

Substituting the values in Eq. (1), we get

ΔH = 2.1 × 10^-3 + 2 × 2 × 300 = 3300 cal

We know

ΔG = ΔH − T ΔS ...(2)

Substituting the values in Eq. (2), we get

ΔG = 3300 - 300 × 20

= -2700 cal = - 2.7 kcal

Q.58. The standard heat of formation (Δ_fH⁰₂₉₈) of ethane (in kJ mol^–1), if the heat of combustion of ethane, hydrogen and graphite are −1560, −393.5 and −286 kJ mol^–1, respectively is ______.    (2020)

Ans. 192.5

We know,

Standard heat of formation of ethane is Δ_fH

Given:

 ...(1)

 ...(2)

 ...(3)

On applying algebraic operations on equation, that is, 2 × Eq. (3) + 3 × Eq. (2) – Eq. (1), We get,

Q.59. The magnitude of work done by a gas that undergoes a reversible expansion along the path ABC shown in the figure is ________.    (2020)

Ans. 48

The magnitude of word done undergo a reversible expansion along the path ABC is the are of the trapezium ABC.

Thus, the word done is

Q.60. At constant volume, 4 mol of an ideal gas when heated from 300 K to 500 K changes its internal energy by 5000 J. The molar heat capacity at constant volume is _____.    (2020)

Ans. 6.25

We know

ΔU = nC_V,mΔT ...(1)

Substituting the given values in Eq. (1), we get

Q.61. If enthalpy of atomization for Br₂(l) is x kJ mol^–1 and bond enthalpy for Br₂ is y kJ mol^–1, the relation between them    (2020)
(a) is x = y
(b) Does not exist
(c)  is x > y
(d) is x < y

Ans. c

Given, enthalpy of atomization of B₂(l) is x kJ mol^–1 and bond enthalpy of B₂(l) is y kJ mol^–1

From the above two reactions

x = Δ_vap H + y

⇒ x > y.

Q.62. The true statement amongst the following is    (2020)
(a) Both ΔS and S are functions of temperature.
(b) Both S and ΔS are not functions of temperature.
(c) S is not a function of temperature but ΔS is a function of temperature.
(d) S is a function of temperature but ΔS is not a function of temperature.

Ans. a

Both entropy (S) and change in entropy (ΔS) is the function of temperature.

 

Q.63. Consider the reversible isothermal expansion of an ideal gas in a closed system at two different temperatures T₁ and T₂ (T₁ < T₂). The correct graphical depiction of the dependence of work done (w) on the final volume (V) is:    (2019)
(a) 

(b) 

(c) 

(d) |

Ans. b

⇒

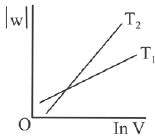
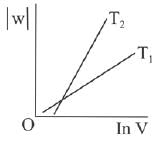
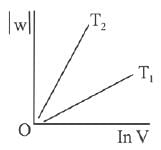
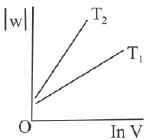
|w| = nRT (InV₂ - InV₁)

|w| = nRT In V₂ - nRT V₁

y = mx + c

So, slope of curve 2 is more than curve 1 and intercept of curve 2 is more negative than curve 1.

Q.64. The entropy change associated with the conversion of 1 kg of ice at 273 K to water vapours at 383 K is: (Specific heat of water liquid and water vapour are 4.2 kJ K^-1 kg^-1 and 2.0 kJ K^-1 kg^-1; heat of liquid fusion and vapourisation of water are 334 kJ kg^-1 and 2491 kJ kg^-1, respectively).
(log 273 = 2.436, log 373 = 2.572, log 383 = 2.583)    (2019)
(a) 7.90 kJ kg^-1 K^-1
(b) 2.64 kJ kg^-1 K^-1
(c) 8.49 kJ kg^-1 K^-1
(d) 9.26 kJ kg^-1 K^-1

Ans. d

As we know,

Also,

Also,

Now,

 

∴ Total entropy change

ΔS = 9.26 kJ kg^-1 K^-1

Q.65. A process has ΔH = 200 J mol^-1 and ΔS = 40 JK^-1 mol^-1. Out of the values given below, choose the minimum temperature above which the process will be spontaneous:    (2019)
(a) 20 K
(b) 12 K
(c) 5 K
(d) 4 K

Ans. c

ΔH = 200 J mol^-1

ΔS = 40 JK^-1 mol^-1

For spontaneous reaction,

ΔG < 0

ΔH - TΔS < 0; ΔH < TΔS

5 < T

So, minimum temperature is 5 K.

Q.66. The process with negative entropy change is:    (2019)
(a) Dissociation of CaSO₄(s) to CaO(s) and SO₃(g)
(b) Sublimation of dry ice
(c) Dissolution of iodine in water
(d) Synthesis of ammonia from N₂ and H₂

Ans. d

In the process of synthesis of ammonia from N₂ and H₂, number of moles decreases which implies that the change in entropy will be negative.

N₂(g) + 3H₂(g) → 2NH₃(g)

Q.67. An ideal gas undergoes isothermal compression from 5 m³ to 1 m³ against a constant external pressure of 4 Nm^-2. Heat released in this process is used to increase the temperature of 1 mole of Al. If molar heat capacity of Al is 24 J mol^-1 K^-1, the temperature of Al increases by:    (2019)
(a) 3/2 K
(b) 2 K
(c) 2/3 K
(d) 1 K

Ans. c

We know that,

w = -P_ext(V_f - V_i)

w = -4 Nm^-2(1 - 5)m³

w = 16 Nm ⇒ 16 J

For isothermal compression,

ΔU = q + w

⇒ q = -w = -16 J (∵ ΔU = 0 for isothermal process)

From calorimetry,

Heat given = n C ΔT

∴ Change in temperature, ΔT = 2/3 K

Q.68. Two blocks of the same metal having same mass and at temperature T₁, and T₂, respectively, are brought in contact with each other and allowed to attain thermal equilibrium at constant pressure. The change in entropy, ΔS, for this process is:    (2019)
(a) 

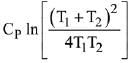
(b) 

(c) 

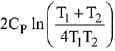
(d) 

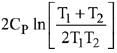
Ans. a

Final temperature

Q.69. For the chemical reaction X ⇌ Y, the standard reaction Gibbs energy depends on temperature T (in K) as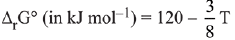

The major component of the reaction mixture at T is:    (2019)
(a) Y if T= 300 K
(b) Y if T= 280 K
(c) X if T = 350 K
(d) X if T = 315 K

Ans. d

At 315 K; ΔGº

ΔG° = 120 - 118.125 = positive

Since ΔG° is positive then K_eq < 1.

Q.70. The standard reaction Gibbs energy for a chemical reaction at an absolute temperature T is given by ΔG° = A - BT where A and B are non-zero constants. Which of the following is true about this reaction?    (2019)
(a) Exothermic if B < 0
(b) Endothermic if A > 0
(c) Endothermic if A < 0 and B > 0
(d) Exothermic if A > 0 and B < 0

Ans. c

MgO (s) + C(s) → Mg (s) + CO (g)

For a reaction to be spontaneous

ΔG < 0

ΔH° - TΔS° < 0

T > 2480.3 K

Q.71. For a diatomic ideal gas in a closed system, which of the following plots does not correctly describe the relation between various thermodynamic quantities?    (2019)
(a) 

(b) 

(c) 

(d) 

Ans. b

ΔG° = A - BT

A and B are non-zero constants

∴ ΔG° = ΔH° - TΔS° = A - BT

∴ Reaction will be endothermic if ΔG° > 0.

Hence, A > O and B < O.

Q.72. Given: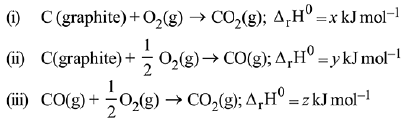

Based on the above thermochemical equations, find out which one of the following algebraic relationships is correct?    (2019)
(a) x = y + z
(b) z = x + y
(c) y = 2z - x
(d) x = y - z

Ans. a

(ΔT_f)x = (ΔT_f)_y

K_f.m_x = K_f.m_y

m_y = 3.27 A; y ≈ 3A

Q.73. For silver, C_p(JK^-1 mol^-1) = 23 + 0.01T. If the temperature (T) of 3 moles of silver is raised from 300 K to 1000 K at 1 atm pressure, the value of ΔH will be close to:    (2019)
(a) 62 kJ
(b) 16 kJ
(c) 21 kJ
(d) 13 kJ

Ans. a

Given: n = 3

T₁ = 300; T₂ = 1000

C_p =23 + o.01T

The relation between ΔH and C is

After putting all variable values in eq. (i)

= 3[16100 + 4550] = 3 × 20650 = 61950 J

= 61.95 kJ

= 62 kJ

Q.74. Which one of the following equations does not correctly represent the first law of thermodynamics for the given processes involving an ideal gas ? (Assume non-expansion work is zero)    (2019)
(a) Cyclic process : q = -w
(b) Adiabatic process: ΔU= -w
(c) Isochoric process: ΔU = q
(d) Isothermal process: q = -w

Ans. b

From first law of thermodynamics, ΔU = q + w

For adiabatic process, q = 0

∴ ΔU = w

For isothermal process, ΔU = 0

For cyclic process, ΔU = 0

For isochoric process, w = 0

Q.75. 5 moles of an ideal gas at 100 K are allowed to undergo reversible compression till its temperature becomes 200 K. If C_v = 28 J K^-1 mol^-1, calculate ΔU and ΔPV for this process. (R = 8.0 J K^-1 mol^-1)    (2019)

(a) ΔU = 14 kJ; Δ(PV) = 18 kJ

(b) ΔU = 14 kJ; Δ(PV) = 0.8 kJ

(c) ΔU = 14 kJ; Δ(PV) = 4 kJ

(d) ΔU = 14 kJ; Δ(PV) = 8.0 kJ

Ans. c

ΔU = nCv ΔT = 5 × 28 × 100 = 14 KJ

Δ(PV) = nR (T₂ - T₁) = 5 × 8 × 100 = 4 KJ

Q.76. Among the following, the set of parameters that represents path functions, is:    (2019)
(A) q + w
(B) q
(C) w
(D) H-TS
(a) (B) and (C)
(b) (B), (C) and (D)
(c)(A) and (D)
(d) (A), (B) and (C)

Ans. a

We know that heat and work are not state functions but q + w = ΔU is a state function. H -TS (i.e. G) is also a state function.

Q.77. Consider the given plot of enthalpy of the following reaction between A and B, A + B → C + D.
Identify the incorrect statement.    (2019)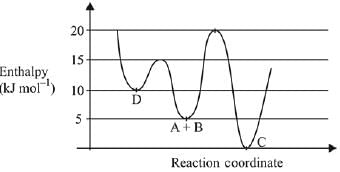

(a) Activation enthalpy to form C is 5kJ mol^-1 less than that to form D.
(b) C is the thermodynamically stable product.
(c) D is kinetically stable product.
(d) Formation of A and B from C has highest enthalpy of activation.

Ans. a

As we can see from the graph that activation enthalpy to form D from A+B is 15 - 5 = 10 kJ mol^-1, whereas, to form C from A + B is 20 - 5 = 15 kJ mol^-1. Therefore, activation enthalpy to form C is 5 kJ more than that to form D.

Q.78. During compression of a spring the work done is 10 kJ and 2 kJ escaped to the surroundings as heat. The change in internal energy, ΔU (in kJ) is:    (2019)
(a) -12
(b) -8
(c) 8
(d) 12

Ans. c

w= 10 kJ

q = -2 kJ

ΔU = q + w = -2 + 10 = 8 kJ

Q.79. A process will be spontaneous at all temperatures if:    (2019)
(a) ΔH < 0 and ΔS < 0
(b) ΔH > 0 and ΔS < 0
(c) ΔH < 0 and ΔS > 0
(d) ΔH > 0 and ΔS > 0

Ans. c

A reaction is spontaneous if ΔG_sys is negative.

ΔG_sys = ΔH_sys -TΔS_sys

A reaction will be spontaneous at all temperatures if ΔH_sys is negative and ΔS_sys is positive.

Q.80. The difference between ΔH and ΔU (ΔH-ΔU), when the combustion of one mole of heptane (I) is carried out at a temperature T, is equal to:    (2019)
(a) -4 RT
(b) -3RT
(c) 4RT
(d) 3 RT

Ans. a

ΔH - ΔU = Δn_gRT

Δn_g = no. of moles of product in gaseous state - no. of moles of reactant in gaseous state.

∵ Δn_g = -4

∴ ΔH - ΔU = -4RT

Q.81. An ideal gas is allowed to expand from 1 L to 10 L against a constant external pressure of 1 bar. The work done in kJ is:    (2019)
(a) -9.0
(b) +10.0
(c) -0.9
(d) -2.0

Ans. c

w = - PΔV

= -(1 bar) x (9 L)

= -(10⁵ Pa) x (9 x 10^-3) m³ 

= - 9 x 10² N.m

= - 900 J

= - 0.9 kJ

Q.82. Enthalpy of sublimation of iodine is 24 cal g^-1 at 200°C. If specific heat of I₂(s) and I₂(vap) are 0.055 and 0.031 cal g^-1K^-1 respectively, then enthalpy of sublimation of iodine at 250°C in cal g^-1 is:    (2019)
(a) 2.85
(b) 5.7 
(c) 22.8
(d) 11.4

Ans. c

I₂(s) → I₂(g).

Heat of reaction depend upon temperature i.e., it varies with temperature, as given by Kirchoff's equation,

where ΔC_p = C_p of product - C_p of reactant

∴ ΔC_p = 0.031 - 0.055 = - 0.024 cal/g

ΔH₍₂₅₀₎ - ΔH₍₂₀₀₎ = -0.024(523 - 473)

ΔH₍₂₅₀₎ = 24 - 50 x 0.024 = 22.8 cal/g

Q.83. The INCORRECT match in the following is:    (2019)
(a) ΔG° < 0, K > 1
(b) ΔG° = 0, K = 1
(c) ΔG° > 0, K < 1
(d) ΔG° < 0, K < 1

Ans. d

ΔGº = -RT Ink

∴ If K > 1 then ΔGº < 0

If K < 1 then ΔGº > 0

If K = 1 then ΔGº = 0

Q.84. Which of the following lines correctly show the temperature dependence of equilibrium constant K, for an exothermic reaction?    (2018)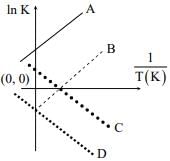

(a) A and B 
(b) B and C 
(c) C and D 
(d) A and D 

Ans. b

ΔGº = -RT In K

ΔHº - TΔSº = -RT In K

Therefore In K vs 1/T graph will be a straight line with slope equal to Since reaction is exothermic, therefore ΔH⁰ itself will be negative resulting in positive slope.

Q.85. The combustion of benzene (1) gives CO₂(g) and H₂O(I). Given that heat of combustion of benzene at constant volume is -3263.9 kJ mol^-1 at 25⁰ C; heat of combust ion (in kJ mol^-1) of benzene at constant pressure will be:    (2018)
(a) 4152.6 
(b) -452.46  
(c) 3260 
(d) -3267.6 

Ans. d

Δng = 6-7.5 = -1.5

ΔH  = ΔU + ΔngRT

= -3263.9 - 1.5 x 8.134 x 10^-3 x 298

= -3267.6

Q.86. An ideal gas undergoes a cyclic process as shown in Figure.

ΔU_BC = −5 KJ mol⁻¹, q_AB = 2KJ mol⁻¹
W_AB = −5KJ mol⁻¹, W_CA = 3KJ mol⁻¹
Heat absorbed by the system during process CA is:    (2018)
(a) -18 KJ mol^-1 
(b) -5 kJ mol^-1 
(c) +5 KJ mol^-1 
(d) 18 KJ  mol^-1 

Ans. c

AB → isobaric

BC → Isochoric

CA → not defined

ΔU_AB = q + W

= 2 − 5 = −3

ΔU_ABC=ΔU_AB+ΔU_BC

=− 3 − 5= − 8 kJ

ΔU_CBA = +8

= Q + W

8 = Q + 3

Q = +5 kJ

 

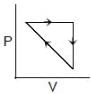
Q.87. For which of the following processes, ΔS is negative?    (2018)
(a) C(diamond) → C(graphite) 
(b) N₂(g, 1 atm) → N₂(g, 5 atm) 
(c) N₂(g, 273 K) → N₂(g, 300 K) 
(d) H₂(g) → 2H(g) 

Ans. b

N₂ (g, 1 atm) → N₂ (g, 5 atm)

for isothermal process

Therefore, ΔS < 0 

Q.88. ΔU is equal to    (2017)
(a) Isochoric work
(b) Isobaric work
(c) Adiabatic work
(d) Isothermal work

Ans. c

For adiabatic process, q = 0

∴ As per 1^st law of thermodynamics,

ΔU = W 

Q.89. For a reaction, A(g) → A(l); ΔH = –3RT.
The correct statement for the reaction is:    (2017)
(a) ΔH = ΔU = 0
(b) |ΔH| < |ΔU|
(c) |ΔH| > |ΔU|
(d) ΔH = ΔU ≠ 0

Ans. c

For the reaction A(g) → A(1)

The change in the number of moles of gaseous species Δn = 0 - 1 = -1

The enthalpy change ΔH = -3RT

ΔH = ΔU + ΔnRT

-3RT = ΔU + (-1)RT

The change in internal energy  ΔU = -2RT

Hence, |ΔH| > |ΔU|

Q.90. The enthalpy change on freezing of 1 mol of water at 5°C to ice at –5°C is:    (2017)

(Given Δ_fus H = 6 kJ mol^-1 at 0ºC,

C_p(H₂O, ℓ) = 75.3 J mol^-1 K^-1,

Cp (H₂O, S) = 36.8 J mol^-1 K^-1)
(a) 6.00 kJ mol^-1
(b) 5.81 kJ mol^-1
(c) 5.44 kJ mol^-1
(d) 6.56 kJ mol^-1

Ans. d

In order to calculate the enthalpy change for H₂O at 5ºC, we need to calculate the enthalpy change of all the transformation involved in the process.

(a) Energy change of 1 mol, H₂O(I), at 5ºC → 1 mol, H₂O(I), 0ºC

(b) Energy change of 1 mol, H₂O(I), at 0ºC → 1 mol, H₂O(s)(ice), 0ºC

(c) Energy change of 1 mol, Ice(s), at 0ºC → 1 mol, Ice(s), -5⁰C

Total ΔH = C_p(H₂O(l)]ΔT +ΔH freezing + C_p [H₂O (s)] ΔT

= (75.3 J mol^-1 K^-1)(-5)K + (-6 x 10³ J mol^-1) + (36.8 J mol^-1 K^-1) (-5) K

ΔH = -6.56 kJ mol^-1 (exothermic process)

So, ΔH = 6.56 kJ

Q.91. A gas undergoes change from state A to state B. In this process, the heat absorbed and work done by the gas is 5 J and 8 J, respectively. Now gas is brought back to A by another process during which 3 J of heat is evolved. In this reverse process of B to A:    (2017)
(a) 6J of the work will be done by the gas
(b) 6J of the work will be done by the surrounding on gas.
(c) 10 J of the work will be done by the surrounding on gas.
(d) 10 J of the work will be done by the gas

Ans. b

Q.92. The heats of combustion of carbon and carbon monoxide are - 393.5 and -283.5 kJ mol^-1, respectively.
The heat of formation (in kJ) of carbon monoxide per mole is:    (2016)
(a) 110.5
(b) 676.5
(c) -676.5
(d) -110.5

Ans. d

Q.93. A reaction at 1 bar is non-spontaneous at low temperature but becomes spontaneous at high temperature. Identify the correct statement about the reaction among the following:    (2016)
(a) Both ΔH and ΔS are negative.
(b) Both ΔH and ΔS are positive.
(c) ΔH is positive while ΔS is negative.
(d) ΔH is negative while ΔS is positive.

Ans. b

ΔG=ΔH−T. ΔS

If ΔH & ΔS are both positive, then ΔG may be negative at height temperature. Hence reaction becomes spontaneous at higher temperature.

Q.94. If 100 mole of H₂O₂ decompose at 1 bar and 300 K, the work done (kJ) by one mole of O₂(g) as it expands against 1 bar pressure is:
2H₂O₂(l) ⇌ 2H₂O(l) + O₂(g)  (R = 8.3 J K^–1 mol^–1)    (2016)
(a) 498.00
(b) 62.25
(c) 124.50
(d) 249.00

Ans. c

2H₂O₂(l) ⇌ 2H₂O(l) + O₂(g)

W = –P_ext (ΔV) = –(nO₂) RT

∵ 100 mol H₂O₂ on decomposition will give 50 mol O₂ 

⇒ W = –(50)(8.3)(300)J

= - 124500 J

W = – 124.5 kJ

⇒ Work done by O₂(g) = 124.5 kJ