Q 1. A particle is executing simple harmonic motion (SHM) of amplitude A, along the x axis, about x = 0. When its potential Energy (P.E.) equals kinetic energy (K.E.), the position of the particle will be (2019)
(1) A/2
(2) A / (2√2)
(3) A/√2
(4) A
Ans: (3)
Solution: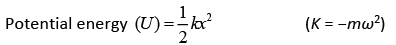
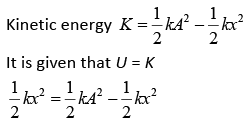
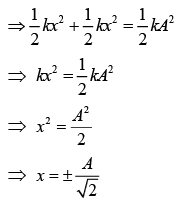
Q 2. A rod of mass M and length 2L is suspended at its middle by a wire. It exhibits torsional oscillations; If two masses each of m are attached at distance L/2 from its center on both sides, it reduces the oscillation frequency by 20%. The value of ratio m/M is close to (2019)
(1) 0.77
(2) 0.57
(3) 0.37
(4) 0.17
Ans: (3)
Solution:
Let ω be the frequency of torsional oscillation.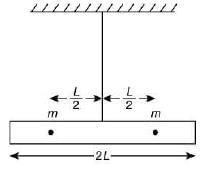
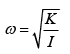
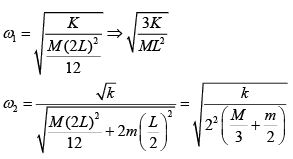
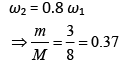
Q 3. A cylindrical plastic bottle of negligible mass is filled with 310 mL of water and left floating in a pond with still water. If pressed downward slightly and released, it starts performing simple harmonic motion at angular frequency ω. If the radius of the bottle is 2.5 cm, then ω is close to (density of water = 103 kg/m3) (2019)
(1) 3.75 rad s−1
(2) 1.25 rad s−1
(3) 2.50 rad s−1
(4) 5.00 rad s−1
Ans: (*)
*Disputed question – None of the options is correct.
Solution:
We know that,
BF = ρAhg
And according to second law of motion we have
ma = B – mg
⇒ −ma = ρA(h + Δh)g – ρAhg
⇒ −ma = ρAgΔh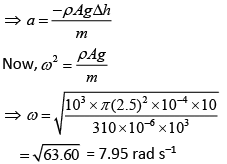
Q 4. A particle executes simple harmonic motion with an amplitude of 5 cm. When the particle is at 4 cm from the mean position, the magnitude of its velocity in SI units is equal to that of its acceleration. Then, its periodic time in seconds is (2019)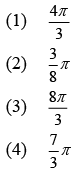
Ans: (3)
Solution:
We have,
a = −ω2x= −ω24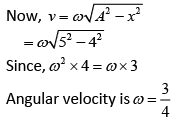
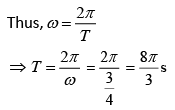
Q 5. A particle undergoing simple harmonic motion has time dependent displacement given by 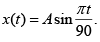 The ratio of kinetic to potential energy of this particle at t = 210 s will be (2019)
The ratio of kinetic to potential energy of this particle at t = 210 s will be (2019)
(1) 2
(2) 1/3
(3) 1
(4) 3
Ans: (2)
Solution: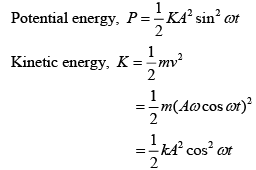
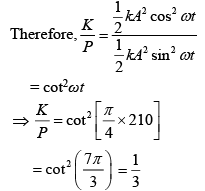
Q 6. A simple pendulum of length 1 m is oscillating with an angular frequency 10 rad/s. The support of the pendulum starts oscillating up and down with a small angular frequency of 1 rad/s and an amplitude of 10−2 m. The relative change in the angular frequency of the pendulum is best given by (2019)
(1) 10−3rad/s
(2) 1 rad/s
(3) 10−1 rad/s
(4) 10−5 rad/s
Ans: (1)
Solution:
Angular frequency of pendulum is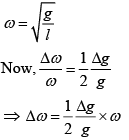
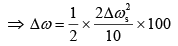 [Δg is due to oscillation of support]
[Δg is due to oscillation of support]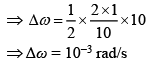
Q 7. A pendulum is executing simple harmonic motion and its maximum kinetic energy is K1. If the length of the pendulum is doubled and it performs simple harmonic motion with the same amplitude as in the first case, its maximum kinetic energy is K2. Then (2019)
(1) K2 = 2K1
(2) K2 = K1/2
(3) K2 = K1/4
(4) K2 = K1
Ans: (1)
Solution: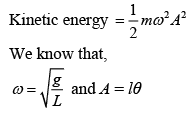
So, the above equation becomes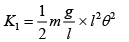
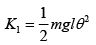 (1) [θ = angular amplitude]
(1) [θ = angular amplitude]
If length is doubled then KE will be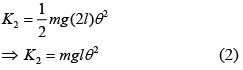
From Eq. (1) and Eq. (2), we get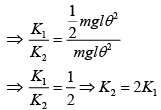
Q 8. The mass and the diameter of a planet are 3 times the respective values for the Earth. The period of oscillation of a simple pendulum on the Earth is 2 s. The period of oscillation of the same pendulum on the planet would be (2019)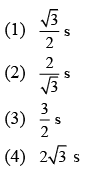
Ans: (4)
Solution:
According to the relation of G gravitational constant and g acceleration due to gravity, we have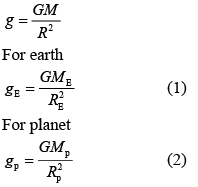
Dividing Eq. (2) by Eq. (1), we get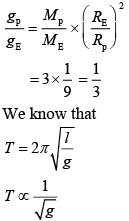
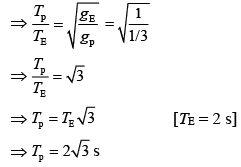
Q 9. A traveling harmonic wave is represented by the equation y(x, t) = 10−3sin(50t + 2x), where x and y are in meter and t is in seconds. Which of the following is a correct statement about the wave? (2019)
(1) The wave is propagating along the negative x-axis with speed 25 ms-1.
(2) The wave is propagating along the positive x-axis with, speed 100 ms−1.
(3) The wave is propagating along the positive x-axis with speed 25 ms−1.
(4) The wave is propagating along the negative x-axis with speed 100 ms−1.
Ans: (1)
Solution:
We know that
y = a sin (ωt + kx)
Given, y = 10−3sin(50t + 2x)
On comparing both the equations, we get
a = 10−3, ω = 50, k = 2
Thus, wave is propagating along negative x-axis with speed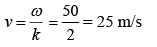
Q 10. Two light identical springs of spring constant k are attached horizontally at the two ends of a uniform horizontal rod AB of length l and mass m. The rod is pivoted at its center O and can rotate freely in horizontal plane. The other ends of the two springs are fixed to rigid supports as shown in figure. The rod is gently pushed through a small angle and released. The frequency of resulting oscillation is (2019)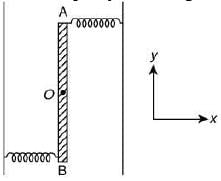
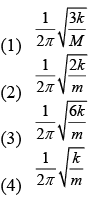
Ans: (3)
Solution: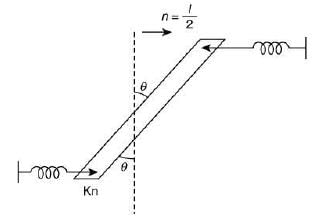
According the relation between Torque and Moment of Inertia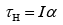
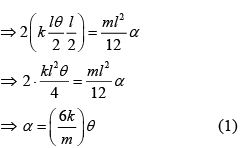
We know that, α = ω2θ (2)
On comparing Eq. (1) and Eq. (2), we get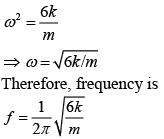
Q 11. A simple pendulum, made of a string of length l and a bob of mass m, is released from a small angle θ0. It strikes a block of mass M, kept on a horizontal surface at its lowest point of oscillations, elastically. It bounces back and goes up to an angle θ1. Then, M is given by (2019)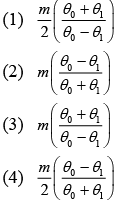
Ans: (3)
Solution:
Let velocity of bob at B is u, which is released by conservation of energy at Point A and B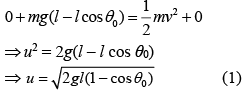
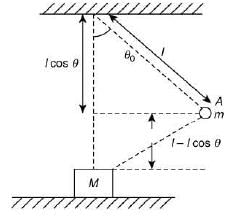
Let velocity of bob after the collision is v.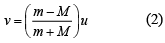
By conservation of energy at Point B and C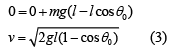
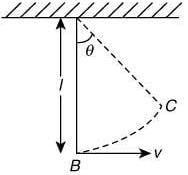
Substituting the value of v and u in Eq. (2), we get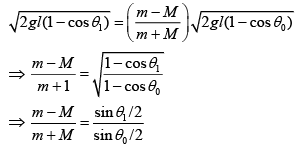
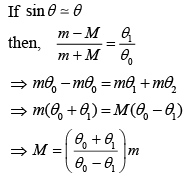
Q 12. A simple harmonic motion is represented by
y = 5(sin 3πt+ 3 cos 3πt) cm
The amplitude and time period of the motion are (2019)
Ans: (1)
Solution:
We have
y = 5(sin 3πt+ 3 cos 3πt)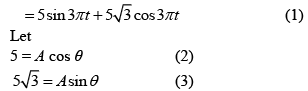
By squaring and adding Eq. (2) and Eq. (3), we get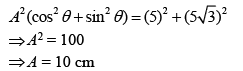
Substituting the value of Eq. (2) and Eq. (3) in Eq. (1), we have
y = A cos θ sin 3πt + A sin θ cos 3πt
⇒ y = A sin (3πt + θ) (4)
⇒ y = 10 sin (3πt + θ)
General wave equation is
y = a sin (ωt + kx)
On comparing with Eq. (4), we get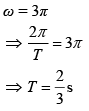
Q 13. A silver atom in a solid oscillates in simple harmonic motion in some direction with a frequency of 1012/sec. What is the force constant of the bonds connecting one atom with the other ? (Mole wt. of silver = 108 and Avagadro number = 6.02 x 1023 gm mole-1) (2018)
(1) 6.44 N/m
(2) 7.1 N/m
(3) 2.2 N/m
(4) 5.5 N/m
Ans: (2)
Solution: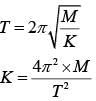
Q 14. An oscillator of mass M is at rest in the equilibrium position in a potential V = 1/2 k(x – X)2. A particle of mass m comes from right with speed u and collides completely inelastically with M and sticks to it. This process repeats every time the oscillator crosses its equilibrium position. The amplitude of oscillations after 13 collisions is : (M = 10, m = 5, u = 1, k = 1) (2018)
(1) 2/3
(2) 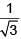
(3) 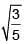
(4) 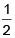
Ans: (2)
Solution:
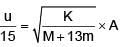
In first collision mu momentum will be imparted to system. In second collision when momentum of (M + m) is in opposite direction mu momentum of particle will make its momentum zero. on 13th collision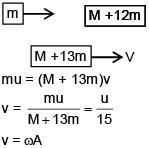
⇒ 
⇒ 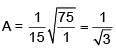
Q 15. A particle executes simple harmonic motion and is located at x = a, b and c at times t0, 2t0 and 3t0 respectively. The frequency of the oscillation is : (2018)
(1) 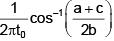
(2) 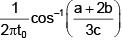
(3) 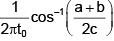
(4) 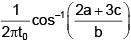
Ans: (1)
Solution:
a = Asinωt0
b = Asin2ωt0
c = Asin3ωt0
a + c = A[sinωt0 + sin3ωt0] = 2Asin2ωt0cosωt0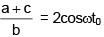
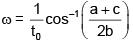
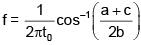
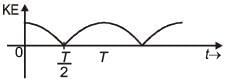
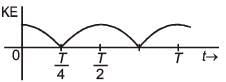
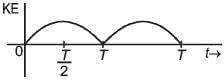
Q 16. A particle is executing simple harmonic motion with a time period T. At time t = 0, it is at its position of equilibrium. The kinetic energy-time graph of the particle will look like : (2017)
(1)
(2)
(3)
(4)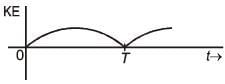
Ans: (2)
Solution: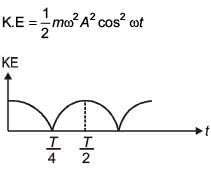
Q 17. A magnetic needle of magnetic moment 6.7 × 10-2 Am2 and moment of inertia 7.5 × 10-6 kg m2 is performing simple harmonic oscillations in a magnetic field of 0.01 T. Time taken for 10 complete oscillations is (2017)
(1) 6.98 s
(2) 8.76 s
(3) 6.65 s
(4) 8.89 s
Ans: (3)
Solution:
For 10 oscillations,
t = 10T = 2π × 1.06
= 6.6568 ≈ 6.65 s
Q 18. A steel rail of length 5 m and area of cross section 40 cm2 is prevented from expanding along its length while the temperature rises by 10°C. If coefficient of linear expansion and Young's modulus of steel are 1.2 × 10-5 K-1 and 2 × 1011 Nm-2 respectively, the force developed in the rail is approximately : (2017)
(1) 2 × 107 N
(2) 2 × 109 N
(3) 3 × 10-5 N
(4) 1 × 105 N
Ans: 4
Solution:
F = yA ∝ Δt
= 2 × 1011 × 40 × 10-4 × 1.2 × 10-5 × 10
= 9.6 × 104 = 1 × 105 N
Q 19. A car is standing 200 m behind a bus, which is also at rest. The two start moving at the same instant but with different forward accelerations. The bus has acceleration 2 m/s2 and teh car has acceleration 4 m/s2. The car will catch up with the bus after at time of - (2017)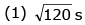
(2) 15 s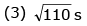
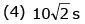
Ans: 4
Solution: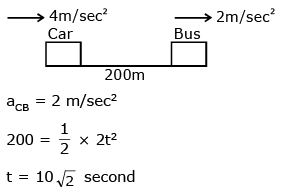
Q 20. A block of mass 0.1 kg is connected to an elastic spring of spring constant 640 Nm-1 and oscillates in a damping medium of damping constant 10–2 kg s-1. The system dissipates its energy gradually. The time taken for its mechanical energy of vibration to drop to half of its initial value, is closest to - (2017)
(1) 2 s
(2) 5 s
(3) 7 s
(4) 3.5 s
Ans: (4)
Solution: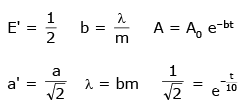
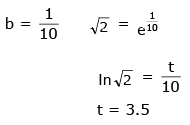
Q 21. In an experiment to determine the period of a simple pendulum of length 1m, it is attached to different spherical bobs of radii r1 and r2. The two spherical bobs have uniform mass distribution.
If the relative difference in the periods, is found to be 5 × 10-4 s, the difference in radii, |r1 – r2| is best given by - (2017)
(1) 0.01 cm
(2) 0.1 cm
(3) 0.5 cm
(4) 1 cm
Ans: 2
Solution: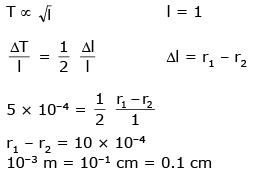
Q 22. A particle performs simple harmonic motion with amplitude A. Its speed is trebled at the instant that it is at a distance 2A/3 from equilibrium position. The new amplitude of the motion is: (2016)
(1) 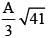
(2) 3A
(3) A√3
(4) 7A/3
Ans: D
Solution:
mω2 = k
Total initial energy = 1/2 kA2
at x = 2A/3, potential energy = 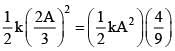
Kinetic energy at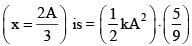
If speed is tripled, new Kinetic energy = 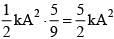
∴ New total energy = 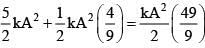
If next amplitude = A'; then 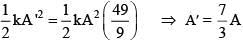
Q 23. In an engine the piston undergoes vertical simple harmonic motion with amplitude 7cm. A washer rests on top of the piston and moves with it. The motor speed is slowly increased. The frequency of the piston at which the washer longer stays in contact with the piston, is closed to: (2016)
(1) 0.7 Hz
(2) 1.2 Hz
(3) 1.9 Hz
(4) 0.1 Hz
Ans. (3)
Solution: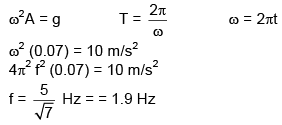
FAQs on Previous Year Questions (2016-2025): Simple Harmonic Motion (Oscillations) - JEE Main
| 1. What is simple harmonic motion? |  |
| 2. How can we mathematically describe simple harmonic motion? |  |
| 3. What is the relationship between the period and frequency of simple harmonic motion? |  |
| 4. How is the displacement, velocity, and acceleration related in simple harmonic motion? |  |
| 5. What is the relationship between the period and the mass of an object undergoing simple harmonic motion? |  |




















