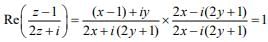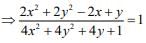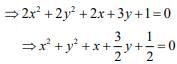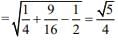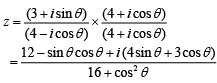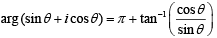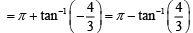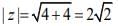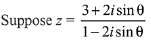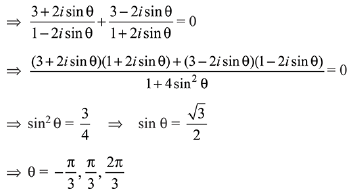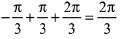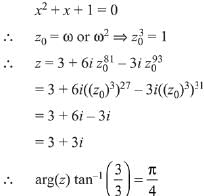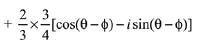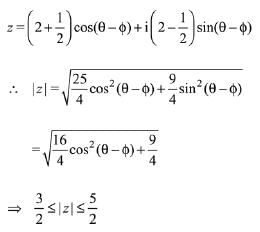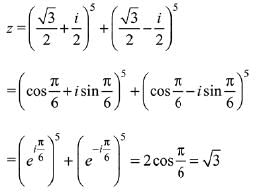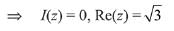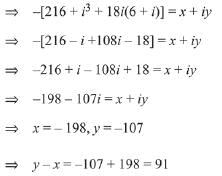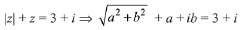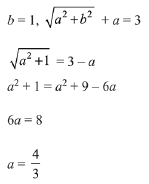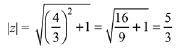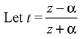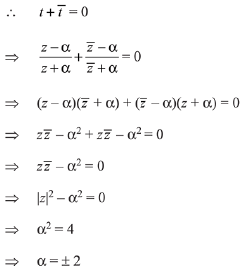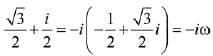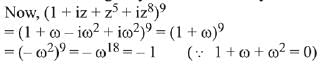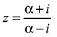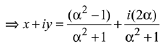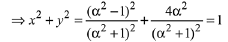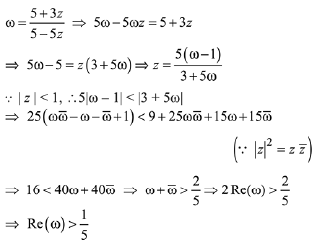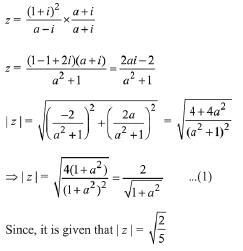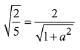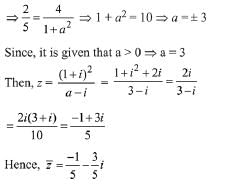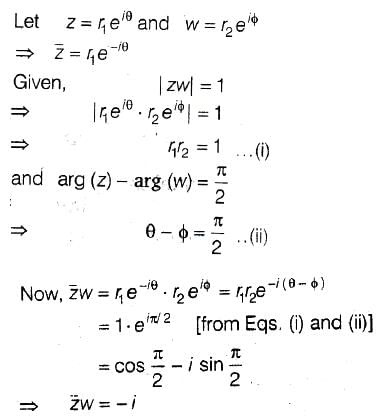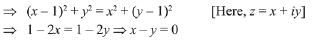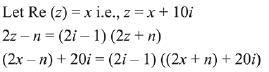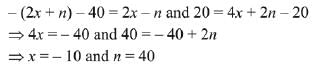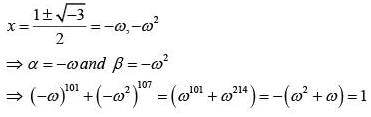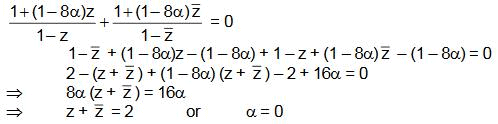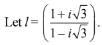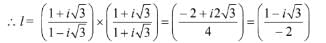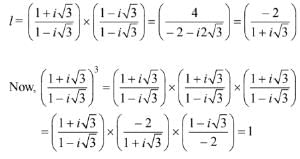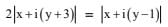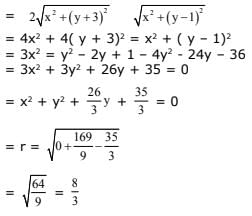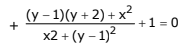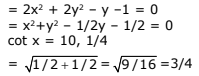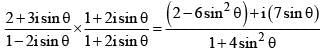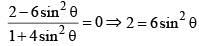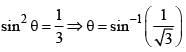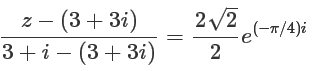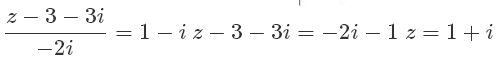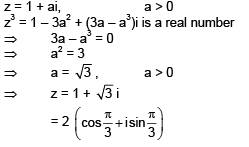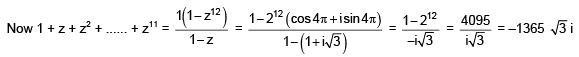JEE Main Previous Year Questions (2016- 2025): Complex Numbers PDF Download

Q.1. If 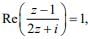 where z = x + iy, then the point (x, y) lies on a    (2020)
(a) Circle whose centre is at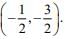
(b) Straight line whose slope is -2/3.
(c) Straight line whose slope is 3/2.
(d) Circle whose diameter is √5/2.

Ans. d
We have
 ...(1)



Therefore,
Center  and radius
Hence, the diameter of circle is √5/2.

Q.2. If 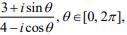is a real number, then an argument of sinθ + i cosθ is    (2020)
(a) π - tan^-1(4/3)
(b) π - tan^-1(3/4)
(c) - tan^-1(3/4)
(d) - tan^-1(4/3)

Ans. a
 We have

Given that the number is real, then
4 sinθ + 3 cosθ = 0 ⇒ tan θ = -3/4
Hence, the argument of sinθ + i cosθ is

Q.3. If z be a complex number satisfying |Re(z)| + |Im(z)| = 4, then |z| cannot be    (2020)
(a)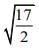
(b) √10
(c) √7
(d) √8

Ans. c
Let the complex number be z = x + iy. So,
|x|+|y| = 4   (1)
Now,

Minimum value of
Maximum value of |z| = 4
So, |z| ∈ (2√2, 4). 

Hence, the value of |z| cannot be √7.

Q.4. Let 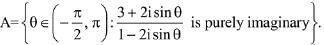 Then the sum of the elements in A is:   (2019)
(a) 5π/6
(b) π
(c) 3π/4
(d) 2π/3

Ans. d

Since, z is purely imaginary, then

Now, the sum of elements in A =

Q.5. Let z₀ be a root of the quadratic equation,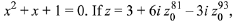 then arg z is equal    (2019)
(a) π/4
(b) π/6
(c) π/3
(d) 0

Ans. a
∵ z₀ is a root of quadratic equation

Q.6. Let z₁ and z₂ be any two non-zero complex numbers such that 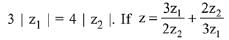 ,then:    (2019)
(a) Re(z) = 0
(b)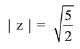
(c)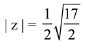
(d) Im(z) = 0

Ans. Bonus

Q.7. Let 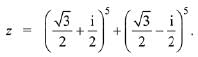 If R(z) and I(z) respectively denote the real and imaginary parts of z, then:    (2019)
(a) I(z) = 0
(b) R(z) > 0 and I(z) > 0
(c) R(z) < 0 and I(z) > 0
(d) R(z) = -(3)

Ans. a

Q.8. Let 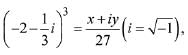 where x and y are real numbers then y - x equals:    (2019)
(a) 91    
(b) -85
(c) 85   
(d) -91

Ans. a

Q.9. Let z be a complex number such that |z| + z = 3 + i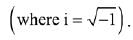
Then |z| is equal to:   (2019)
(a)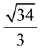
(b) 5/3
(c)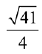
(d) 5/4

Ans. b
Since, |z| + z = 3 + i
Let z = a + ib, then

Compare real and imaginary coefficients on both sides

Then,

Q.10. 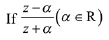 is a purely imaginary number and |z| = 2, then a value of α is:    (2019)
(a) 2
(b) 1
(c) 1/2
(d)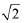

Ans. a

∵ t is purely imaginary number.

Q.11. Let z₁ and z₂ be two complex numbers satisfying |z₁| = 9 and |z₂- 3 - 4i|=4. Then the minimum value of |z₁ -z₂| is:    (2019)
(a) 0    
(b) √2
(c) 1    
(d) 2

Ans. a
|Z₁| = 9, |z₂ - 3 - 4i| = 4
z₁ lies on a circle with centre C₁(0, 0) and radius r₁ = 9
z₂ lies on a circle with centre C₂(3, 4) and radius r₂ = 4
So, minimum value of |z₁ -z₂| is zero at point of contact (i.e. A)

Q.12. If 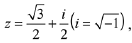 then (1 + iz + z⁵ + iz⁸)⁹ is equal to:
(a) 0    
(b) 1
(c) (-1 + 2i)⁹    
(d) -1

Ans. d
 
where ω is imaginary cube root of unity.

Q.13. All the points in the set 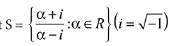 lie on a:    (2019)
(a) straight line whose slope is 1.
(b) circle whose radius is 1.
(c) circle whose radius is √2 .
(d) straight line whose slope is -1.

Ans. b
Let z∈S then
Since, z is a complex number and let z = x + iy
Then,  (by rationalisation)

Then compare both sides
    ...(1)
    ...(2)
Now squaring and adding equations (1) and (2)

Q.14. Let z ∈ C be such that |z| < 1. If ω = 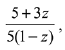 then:    (2019)
(a) 5 Re (ω) > 4    
(b) 4 Im (ω) > 5
(c) 5 Re (ω) >1    
(d) 5 Im (ω) < 1

Ans. c
 

Q.15. If a > 0 and z = 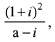 has magnitude  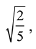then 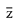 is equal to:    (2019)
(a)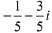
(b)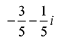
(c)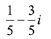
(d)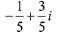

Ans. a

Then, from equation (1),

Now, square on both side; we get

Q.16. If z and ω are two complex numbers such that |zω| = 1 and arg(z) - arg(ω) = π/2, then:    (2019)

(a)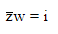
(b)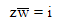
(c)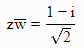
(d)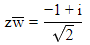

Ans. c

Q.17. The equation 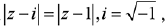 represents:    (2019)
(a) a circle of radius 1/2.
(b) the line through the origin with slope 1.
(c) a circle of radius 1.
(d) the line through the origin with slope -1.

Ans. b
Given equation is, |z - 1| = |z - i|

Hence, locus is straight line with slope 1.

Q.18. Let z ∈ C with Im(z) = 10 and it satisfies 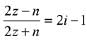 for some natural number n. Then:    (2019)
(a) n = 20 and Re(z) = -10
(b) n = 40 and Re(z) = 10
(c) n = 40 and Re(z) = -10
(d) n = 20 and Re(z) = 10

Ans. c
 
On comparing real and imaginary parts,

Hence, Re(z) = -10

Q.19. If α ,β ∈ c are the distinct roots, of the equation x² - x + 1 =0 , then α¹⁰¹ + β¹⁰⁷ is equal to:    (2018)
(a) -1
(b) 0
(c) 1
(d) 2

Ans. c
 x² - x+ 1 = 0

Q.20. The set of all α ∈ R, for which ω =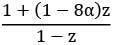is a purely imaginary number, for all z ∈ C Satifying |z| = 1 and Re z ≠ 1, is:    (2018)
(a) An empty set
(b)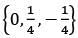
(c) equal to R
(d) {0}

Ans. d
As ω is purely imaginary

If Re(z) ≠ 1
then, α = 0

Q.21. The least positive integer n for which 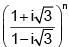 is:    (2018)
(a) 2
(b) 5
(c) 6
(d) 3

Ans. d


Also,

∴ Least positive integer n is 3.

Q.22. Let z ∈ C, the set of complex numbers. Then the equation, 2|z + 3i| – |z – i| = 0  represents a circle with radius    (2017)
(a) a cirlce with radius 8/3
(b) an ellipse with length of minor axis 16/9
(c) an ellipse with length of major axis 16/3
(d) a circle with diameter 10/3

Ans. a

Q.23. The equation 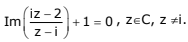represents a part of a circle having radius equal to:    (2017)
(a) 1
(b) 2
(c) 3/4
(d) 1/2

Ans. c
 Let = x + y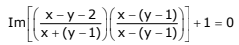
 

Q.24. A value of θ for which 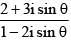is purely imaginary, is:    (2016)
(a) π/3
(b) π/6
(c) sin^-1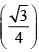
(d) sin^-1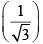

Ans. d

To be purely imaginary if

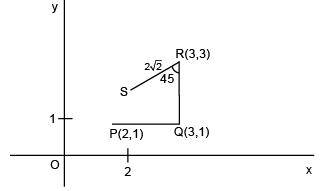
Q.25. The point represented by 2 + i in the Argand plane moves 1 unit eastwards, then 2 units northwards and finally from there 2√2 units in the south- westwards direction. Then its new position in the Argand plane is at the point represented by:    (2016)
(a) 2 + 2i
(b) – 2 – 2i
(c) 1 + i
(d) – 1 – i

Ans. c
Let P(2 + i)
By rotation theorem

Q.26. Let z = 1 + ai be a complex number, a > 0 such that z³ is a real number. Then the sum 1 + z + z² +....+ z¹¹ is equal to    (2016)

(a) -1250 √3 i
(b) 1250 √3 i
(c) -1365 √3 i
(d) 1365 √3 i

Ans. c