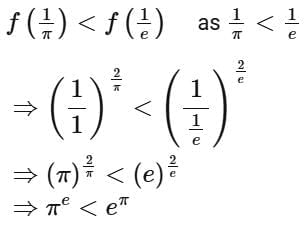JEE Main Previous Year Questions (2016- 2025): Functions | Mathematics (Maths) Class 12 PDF Download
2025
Q1. If the range of the function 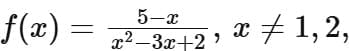 is
is 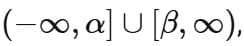 then
then 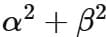 is equal to:
is equal to:
(a) 188
(b) 192
(c) 190
(d) 194
 View Answer
View Answer 
Ans. d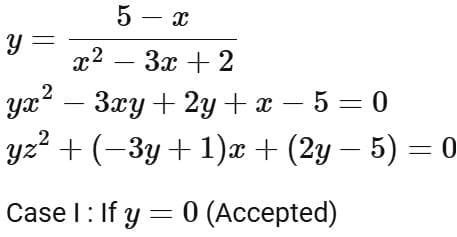
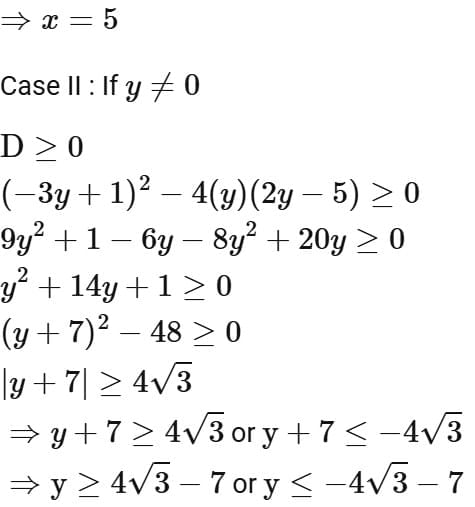
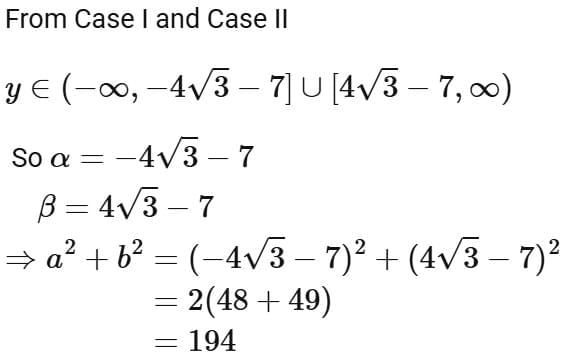
Q2. Let the domains of the functions f(x) = log4 log3 log7 (8 - log2 (x2 + 4x + 5)) and 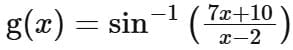 be (α, β) and [γ, δ], respectively. Then α2 + β2 + γ2 + δ2 is equal to:
be (α, β) and [γ, δ], respectively. Then α2 + β2 + γ2 + δ2 is equal to:
(a) 15
(b) 13
(c) 16
(d) 14
 View Answer
View Answer 
Ans. a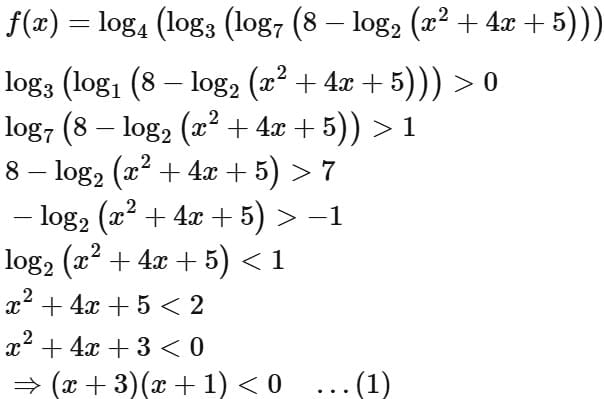
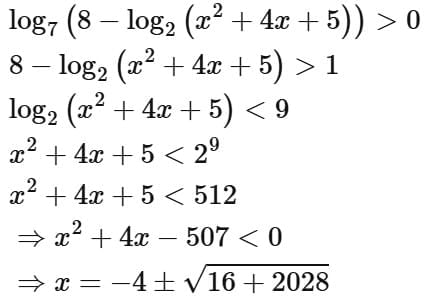
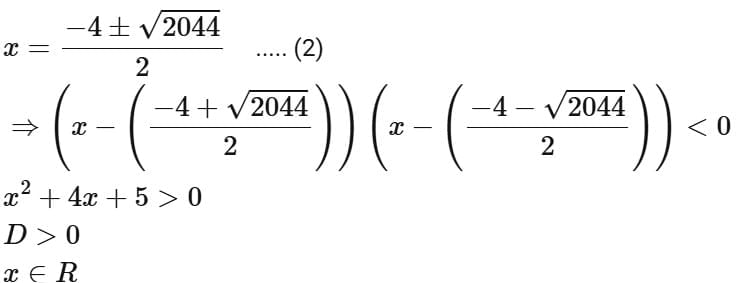
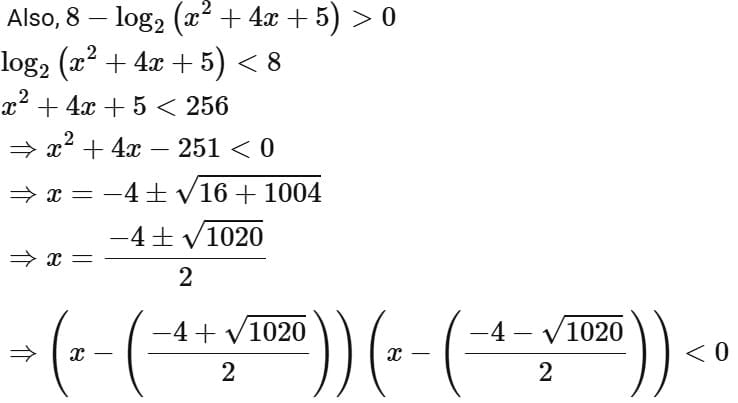
∴ Intersection of (1), (2) and (3)
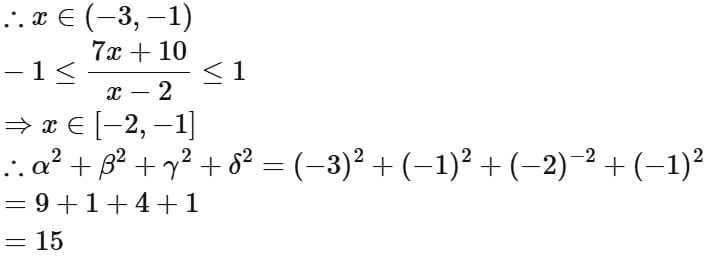
Q3. Let 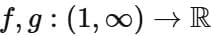 be defined as
be defined as  If the range of the function fog:
If the range of the function fog: 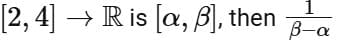 is equal to
is equal to
(a) 56
(b) 2
(c) 29
(d) 68
 View Answer
View Answer 
Ans. a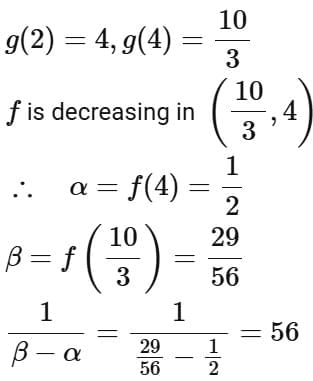
Q4. Let f be a function such that 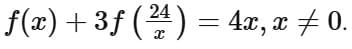 Then f (3) + f (8) is equal to
Then f (3) + f (8) is equal to
(a) 13
(b) 11
(c) 10
(d) 12
 View Answer
View Answer 
Ans. b
Q5. If the domain of the function 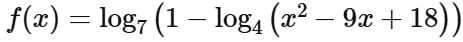 is
is 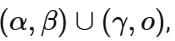 then
then 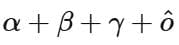 is equal to
is equal to
(a) 17
(b) 15
(c) 16
(d) 18
 View Answer
View Answer 
Ans. d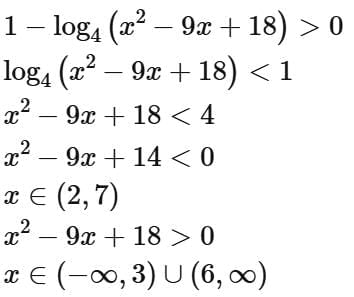

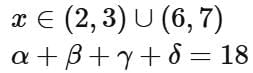
Q6. If the domain of the function 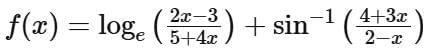 is [α, β) then α2 + 4β is equal to
is [α, β) then α2 + 4β is equal to
(a) 4
(b) 3
(c) 7
(d) 5
 View Answer
View Answer 
Ans. a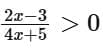
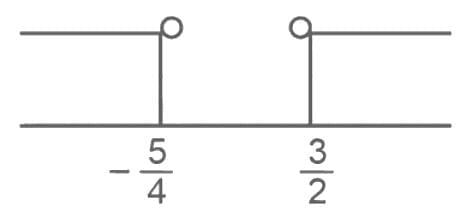
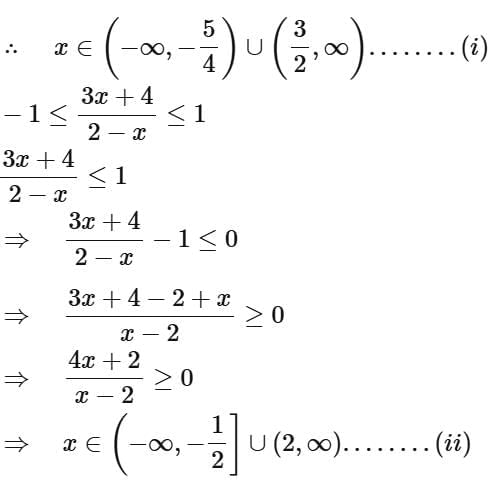
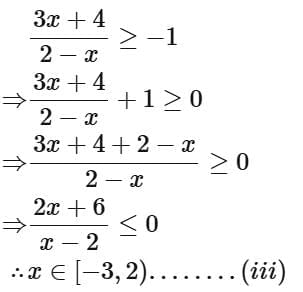
Taking intersection of (i), (ii) and (iii)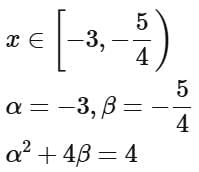
Q7. If the domain of the function 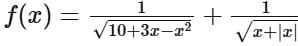 is, (a, b), then (1 + a)2 + b2 is equal to:
is, (a, b), then (1 + a)2 + b2 is equal to:
(a) 29
(b) 30
(c) 25
(d) 26
 View Answer
View Answer 
Ans. d
Similarly,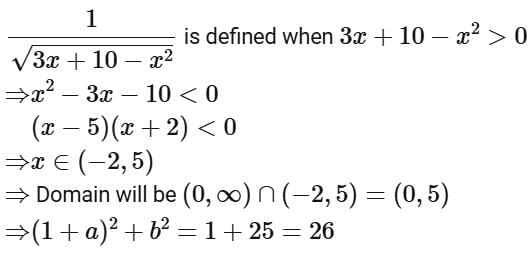
Q8. If the domain of the function log5(18x - x2 - 77) is (α, β) and the domain of the function 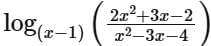 is (γ, δ), then α2 + β2 + γ2 is equal to:
is (γ, δ), then α2 + β2 + γ2 is equal to:
(a) 186
(b) 179
(c) 195
(d) 174
 View Answer
View Answer 
Ans. a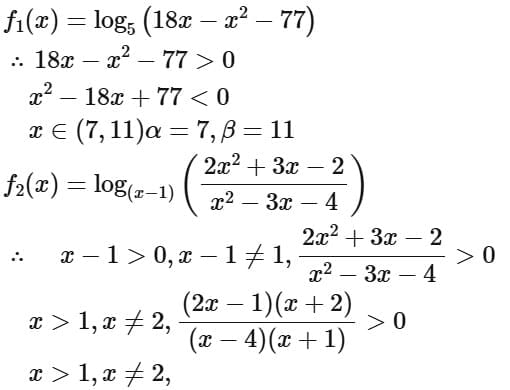
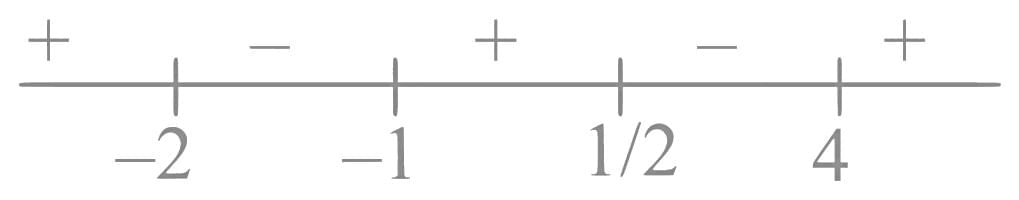
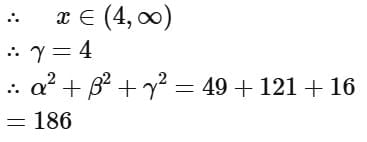
Q9. Let f : [0, 3] → A be defined by f(x) = 2x3 -15x2 +36x + 7 and g : [0,∞) → B be defined by 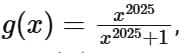 If both the functions are onto and S = {x ∈ Z; x ∈ A or x ∈ B}, then n(S) is equal to:
If both the functions are onto and S = {x ∈ Z; x ∈ A or x ∈ B}, then n(S) is equal to:
(a) 29
(b) 31
(c) 30
(d) 36
 View Answer
View Answer 
Ans. c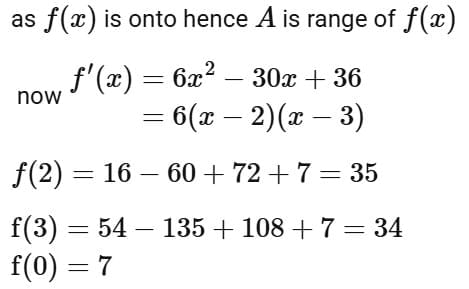
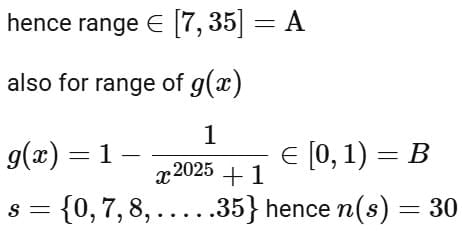
Q10. If 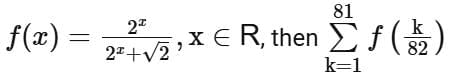 is equal to
is equal to
(a) 82
(b) 81√2
(c) 41
(d) 81/2
 View Answer
View Answer 
Ans. d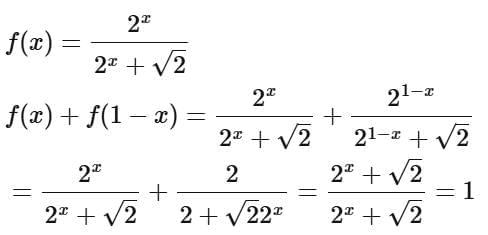
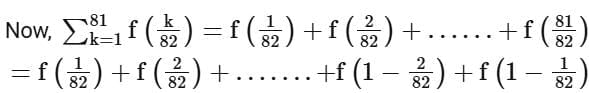
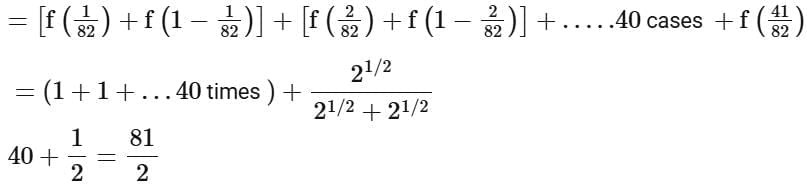
Q11. Let f : R → R be a function defined by 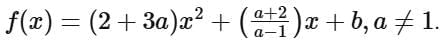 If
If 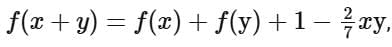 then the value of
then the value of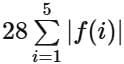 is
is
(a) 735
(b) 675
(c) 715
(d) 545
 View Answer
View Answer 
Ans. b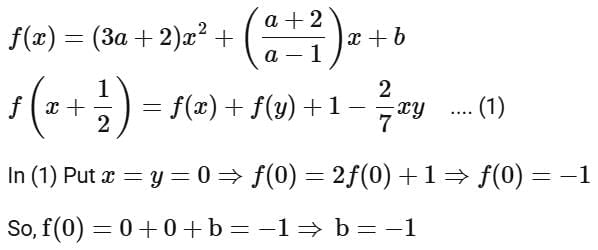
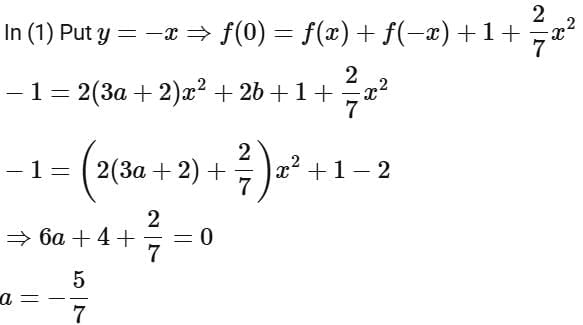
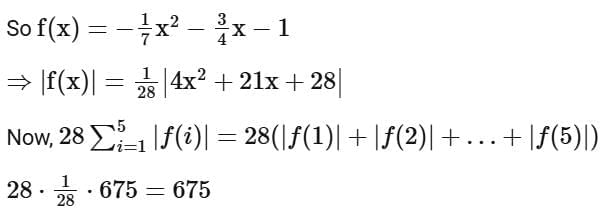
Q12. The function f : (-∞,∞) → (-∞,1) defined by 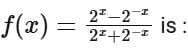
(a) One-one but not onto
(b) Onto but not one-one
(c) Both one-one and onto
(d) Neither one-one nor onto
 View Answer
View Answer 
Ans. a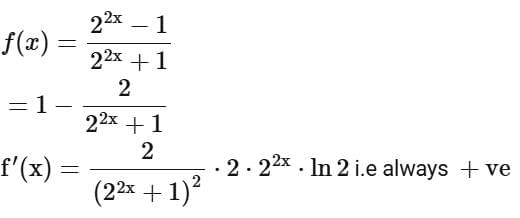
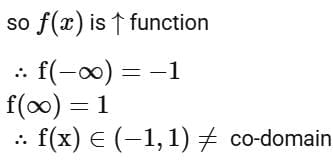
so function is one-one but not onto
Q13. Let 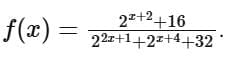 Then the value of
Then the value of 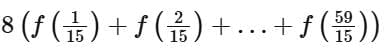 is equal to
is equal to
(a) 108
(b) 92
(c) 118
(d) 102
 View Answer
View Answer 
Ans. c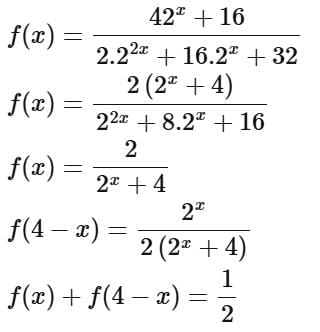
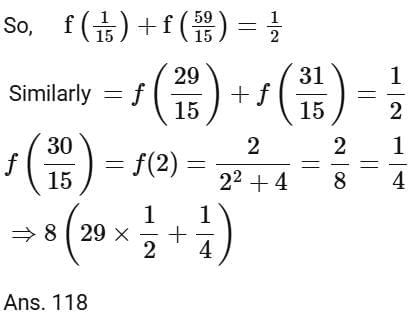
Q14. Let  Then the domain of f o g is
Then the domain of f o g is
(a) (0, ∞)
(b) [1, ∞]
(c) 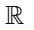
(d) [0, ∞]
 View Answer
View Answer 
Ans. c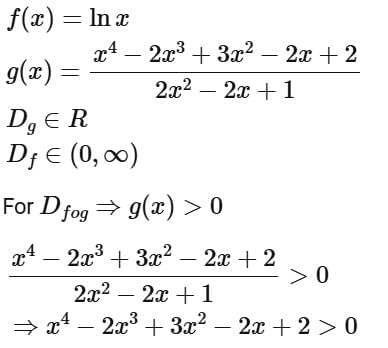
Clearly x < 0 satisfies which are included in option (1) only.
Q15. Let A = {1, 2, 3, 4} and B = {1, 4, 9, 16}. Then the number of many-one functions f : A → B such that 1 ∈ f (A) is equal to:
(a) 151
(b) 139
(c) 163
(d) 127
 View Answer
View Answer 
Ans. a
Step 1: Total Functions with 1 ∈ f (A)
Any function f : A → B where A = {1, 2, 3, 4} and B = {1,4, 9, 16} is defined by choosing one of the four elements of B for each element of A.
Thus, the total number of functions is 44 = 256.
To count those functions where 1 appears at least once in the set f(A), we can use the complementary counting method: subtract the functions that never use 1.
If 1 is excluded, each element of A has only 3 choices (namely, {4, 9, 16}), so the number of such functions is 34 = 81.
Thus, the number of functions such that 1 ∈ f(A) is 256 - 81 = 175.
Step 2: Counting Many-One Functions
In this context, "many-one functions" are understood to be non-injective functions. Since an injective (one-to-one) function from A to B must be a permutation (because both sets have 4 elements), the number of one-to-one functions is 4! = 24.
It is important to note that every injective function f : A → B has f(A) = B (a full permutation) which automatically means 1 ∈ f(A).
Thus, the number of many-one (non-injective) functions f : A → B with 1 ∈ f(A) is found by subtracting the one-to-one functions from the total functions that include 1: 175 - 24 = 151.
This detailed explanation shows that the number of many-one functions f : A → B such that 1 ∈ f(A) is indeed 151.
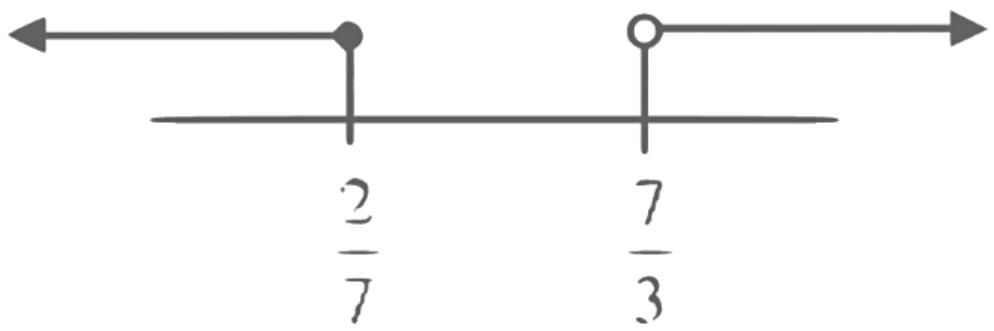
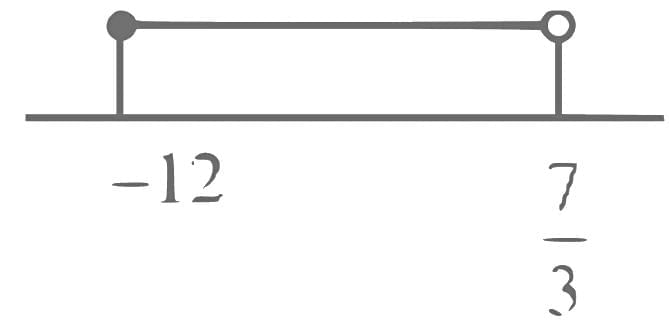
Q16. Let the domain of the function 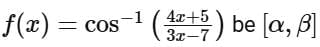 and the domain of
and the domain of 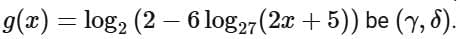
Then |7(α + β) + 4(γ + δ)| is equal to ____________________.
 View Answer
View Answer 
Ans. 96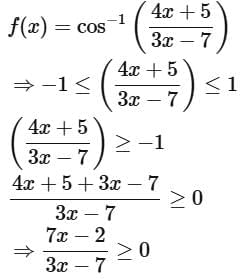
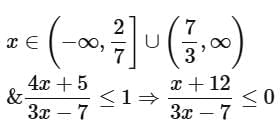

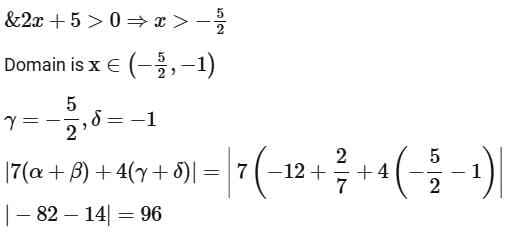
2024
Q1. Let the range of the function 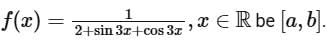 If α and β ar respectively the A.M. and the G.M. of a and b, then α/β is equal to
If α and β ar respectively the A.M. and the G.M. of a and b, then α/β is equal to
(a) π
(b) √π
(c) √2
(d) 2
 View Answer
View Answer 
Ans. c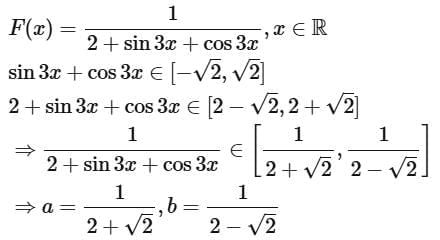
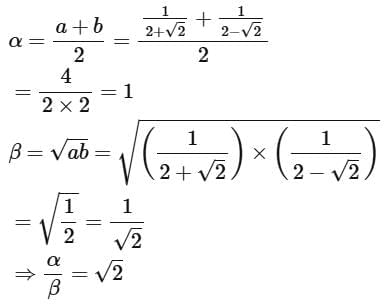
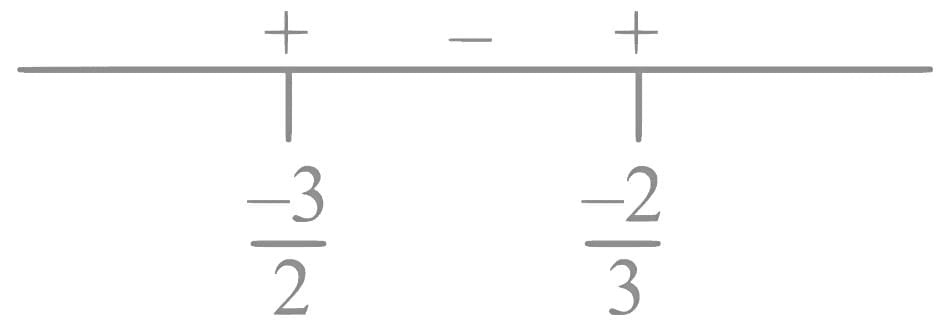
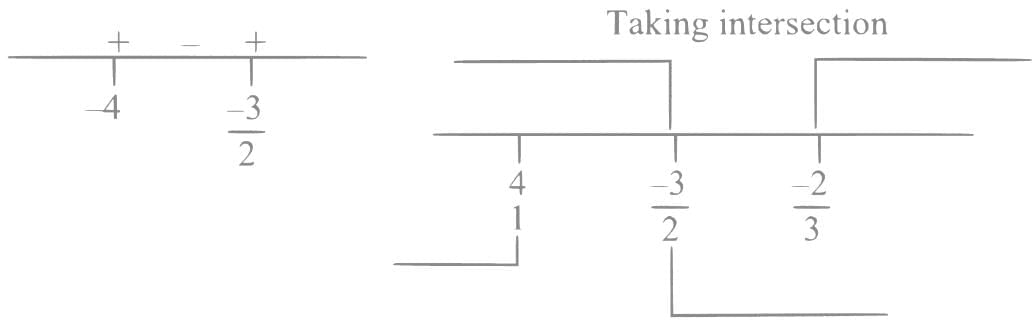
Q2. If the domain of the function 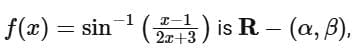 is R - (α, β), then 12 αβ is equal to:
is R - (α, β), then 12 αβ is equal to:
(a) 40
(b) 36
(c) 24
(d) 32
 View Answer
View Answer 
Ans. d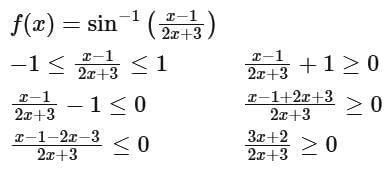
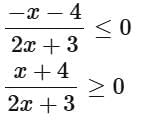
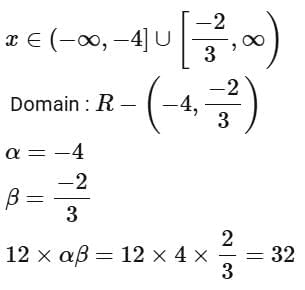
Q3. 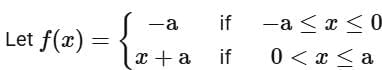 where a > 0 and g(x) = (f(|x|) - |f(x)|)/2. Then the function
where a > 0 and g(x) = (f(|x|) - |f(x)|)/2. Then the function 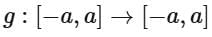 is
is
(a) neither one-one nor onto.
(b) both one-one and onto.
(c) one-one.
(d) onto
 View Answer
View Answer 
Ans. a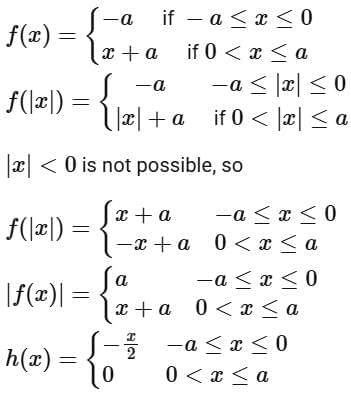
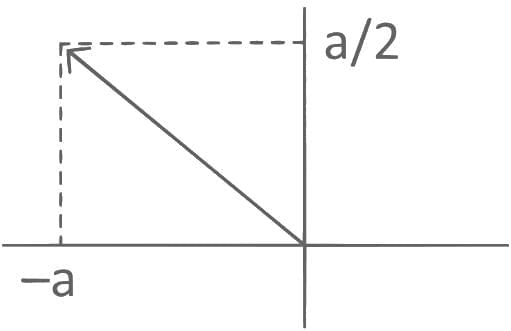 Neither one-one nor onto.
Neither one-one nor onto.
Q4. If the function 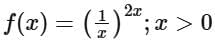 attains the maximum value at x = 1/e then:
attains the maximum value at x = 1/e then:
(a) 
(b) 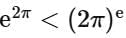
(c) 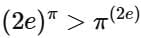
(d) 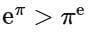
Ans. d
Q5. Let 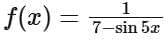 be a function defined on R. Then the range of the function f(x) is equal to:
be a function defined on R. Then the range of the function f(x) is equal to:
(a) 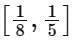
(b) 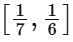
(c) 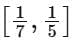
(d) 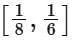
 View Answer
View Answer 
Ans. d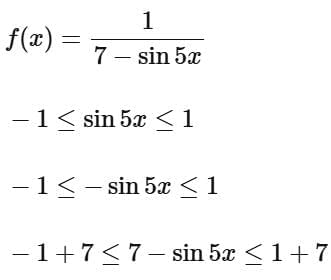
Q6. The function 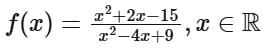 is
is
(a) both one-one and onto.
(b) onto but not one-one.
(c) neither one-one nor onto.
(d) one-one but not onto.
 View Answer
View Answer 
Ans. c
The function 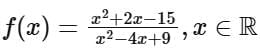 can be simplified to
can be simplified to 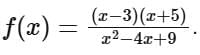
For x = 3 and x = -5, f(x) equals 0.
Therefore, f(x) is not one-one as it yields the same output for different input values.
The range of f(x) is [-2, 1.6], indicating that f(x) does not cover all possible real values.
Consequently, f(x) is not onto.
Thus, the function is neither one-one nor onto.
Q7. Let f, g : R → R be defined as: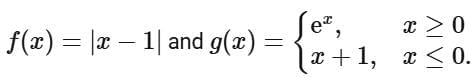
Then the function f(g(x)) is
(a) neither one-one nor onto.
(b) one-one but not onto.
(c) both one-one and onto.
(d) onto but not one-one.
 View Answer
View Answer 
Ans. a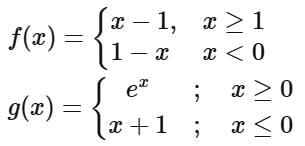
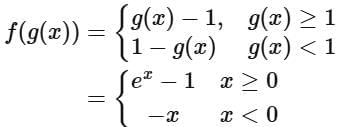
Q8. Let A = {1,3, 7, 9, 11} and B = {2,4,5, 7, 8, 10, 12}. Then the total number of one-one maps f : A → B, such that f(1)+ f(3) =14, is:
(a) 120
(b) 180
(c) 240
(d) 480
 View Answer
View Answer 
Ans. c
f(1)+f(3)=14
Case I
f(1)=2,f(3)=12
f(1)=12,f(3)=2
Total one-one function
=2 × 5 × 4 × 3
=120
Case II
f(1)=4,f(3)=10
f(1)=10,f(3)=4
Total one-one function
= 2 × 5 × 4 × 3
=120
Total cases = 120 + 120 = 240
Q9. If the domain of the function 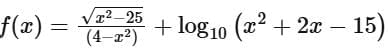 is
is 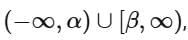 then α2 + β2 is equal to:
then α2 + β2 is equal to:
(a) 140
(b) 175
(c) 125
(d) 150
 View Answer
View Answer 
Ans. d
To find the domain of the function 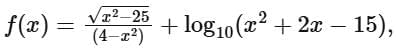 we need to consider the domain conditions for both the square root function and the logarithmic function.
we need to consider the domain conditions for both the square root function and the logarithmic function.
The square root function 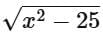 requires that the argument of the square root be non-negative, so x2 - 25 ≥ 0.
requires that the argument of the square root be non-negative, so x2 - 25 ≥ 0.
This inequality is satisfied when x ≤ -5 or x ≥ 5.
The denominator of the rational part of f(x), (4 - x2), cannot be zero, otherwise, the function will become undefined due to division by zero. Thus, we must have 4 - x2 ≠ 0. This inequality is violated when x = ±2.
Combining these conditions gives us the domain for the rational part of the function: x ∈ (-∞,-5] U (5,∞) and x ≠ 2,-2.
Moving on to the logarithmic function, log10(x2 +2x - 15), the argument must be positive: x2 + 2x - 15 > 0.
This is a quadratic inequality, which we can factor to find the solution: (x +5)(x - 3) > 0.
From this, we see that the inequality is satisfied for x < -5 or x > 3.
The overall domain of f(x) is the intersection of the domains for each piece.
Taking the intersection of the two sets gives us: x € (-∞,-5) U (5,∞),
Since the question states that the domain is of the form (-∞, α) U [β, ∞), we can infer that α =- 5 and β = 5.
We calculate α2 + β3 as follows: α2 + β3 = (-5)2 +53 =25 + 125 = 150.
So the correct answer, representing the sum of α2 and β3, is: Option D 150.
Q10. Let f : R → R and g : R → R be defined as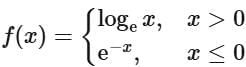 and
and 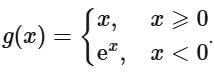
Then, gof : R → R is:
(a) one-one but not onto
(b) neither one-one nor onto
(c) onto but not one-one
(d) both one-one and onto
 View Answer
View Answer 
Ans. b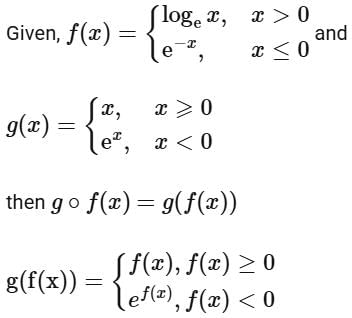
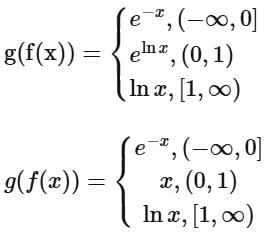
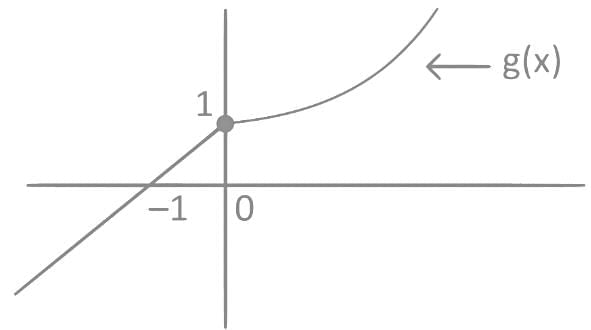
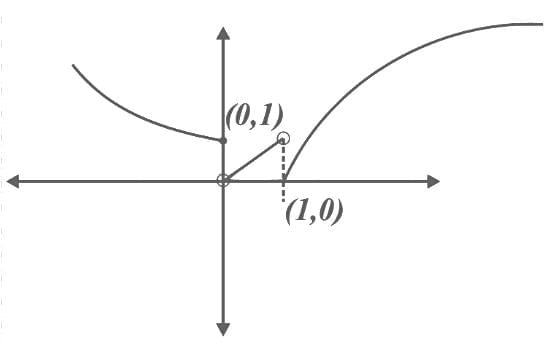 From the graph of g (f(x)), we can say
From the graph of g (f(x)), we can say
g (f(x)) ⇒ Many one into
Q11. If 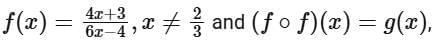 where
where 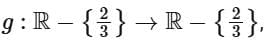 then
then 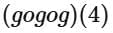 is equal to
is equal to
(a) -4
(b) 19/20
(c) -19/20
(d) 4
 View Answer
View Answer 
Ans. d
To find 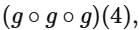 we first need to understand the composition of f with itself, i.e.,
we first need to understand the composition of f with itself, i.e.,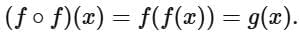 We can then repeatedly apply g to get the given expression.
We can then repeatedly apply g to get the given expression.
First, let's calculate 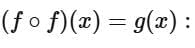
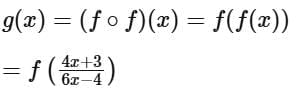
To evaluate this expression, we substitute 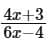 for x in the function f (x):
for x in the function f (x):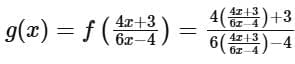
Now, we simplify the expression: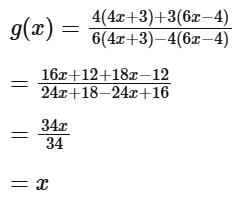
So, g(x) = x for all x in the domain of g, which is R - {2/3}.
It's important to note that the domain restriction is preserved through the composition because f{x} has a vertical asymptote at x = 2/3 which doesn't intersect the graph.
So, g (x) is the identity function on its domain, which means that applying g any number of times will result in the same input for x in the given domain.
Hence, we have: 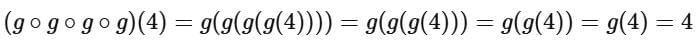
This corresponds to option D, which is 4 .
Q12. If the domain of the function 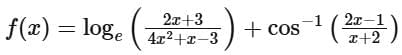 is (α, β), then the value of 5 β - 4α is equal to
is (α, β), then the value of 5 β - 4α is equal to
(a) 9
(b) 12
(c) 11
(d) 10
 View Answer
View Answer 
Ans. b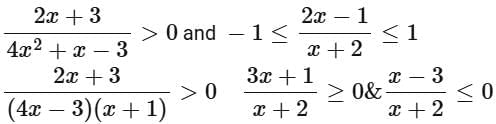
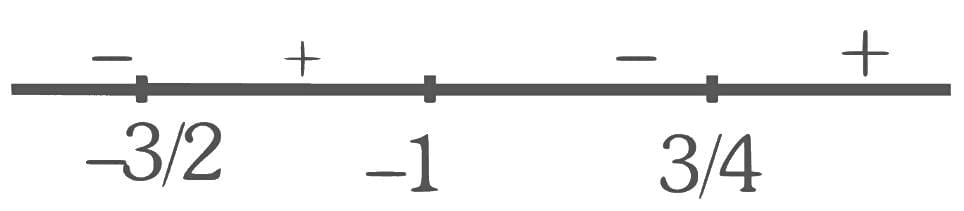
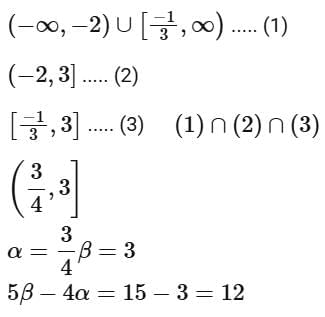
Q13. If the domain of the function 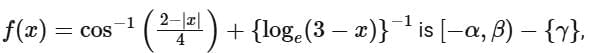 then α + β + γ is equal to:
then α + β + γ is equal to:
(a) 11
(b) 12
(c) 9
(d) 8
 View Answer
View Answer 
Ans. a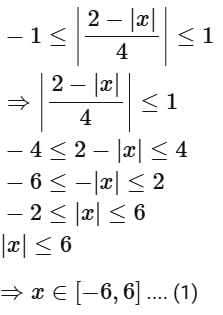
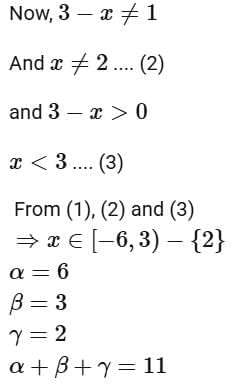
Q14. If 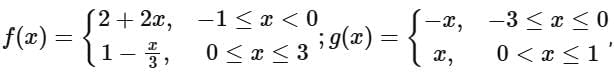 then range of
then range of 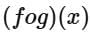 is
is
(a) [0, 1)
(b) [0, 3)
(c) (0, 1]
(d) [0, 1]
 View Answer
View Answer 
Ans. d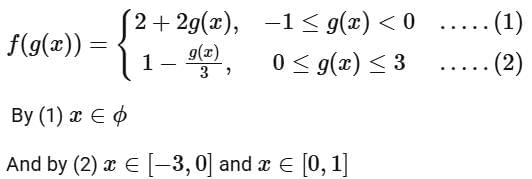
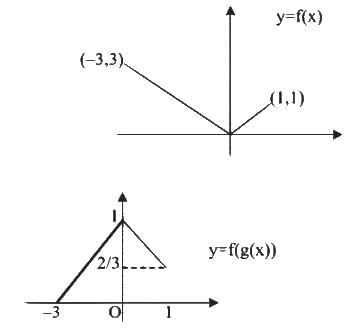
Range of f (g(x)) is [0, 1]
Q15. Let  be defined as
be defined as  Then, the domain of the function fog is:
Then, the domain of the function fog is:
(a) R - {-7/4}
(b) R
(c) 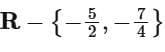
(d) R - {-5/2}
 View Answer
View Answer 
Ans. d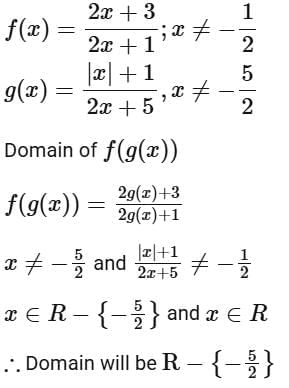
Q16. The function f : N - {1} → N; defined by f (n) = the highest prime factor of n, is:
(a) one-one only
(b) neither one-one nor onto
(c) onto only
(d) both one-one and onto
 View Answer
View Answer 
Ans. b
f : N - {1} → N
f(n) = The highest prime factor of n.
f(2) = 2
f(4) = 2
⇒ many one
4 is not image of any element
⇒ into
Hence many one and into
Neither one-one nor onto.
Q17. Let A = {(x, y) : 2x + 3y = 23, x, y ∈ N} and B = {x : (x, y) ∈ A}. Then the number of one-one functions from A to B is equal to __________.
 View Answer
View Answer 
Ans. 24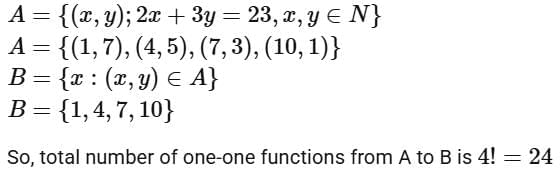
Q18. If a function f satisfies f(m + n) = f(m) + f(n) for all m, n ∈ N and f(1) = 1, then the largest natural number λ such that 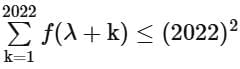 is equal to _________.
is equal to _________.
 View Answer
View Answer 
Ans. 1010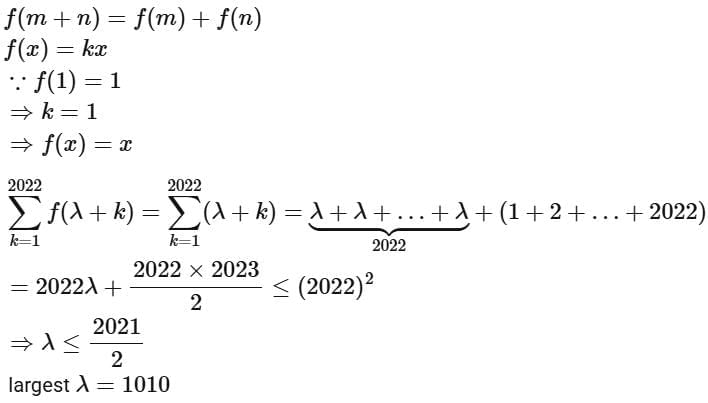
Q19. If the range of 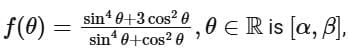 then the sum of the infinite G.P., whose first term is 64 and the common ratio is α/β, is equal to __________.
then the sum of the infinite G.P., whose first term is 64 and the common ratio is α/β, is equal to __________.
 View Answer
View Answer 
Ans. 96
To determine the range of the function 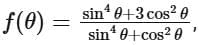 let's start by simplifying the expression.
let's start by simplifying the expression.
Let sin2θ = x, so cos2θ = 1 − x .
The function then transforms into: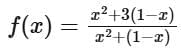
Simplify the numerator and denominator separately: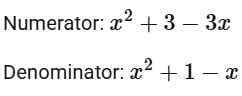
Thus, the function becomes: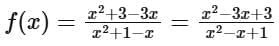
Next, we need to find the range of this function. Let's analyze the function by testing specific values of x in the interval [0 , 1] (since sin2θ ranges from 0 to 1):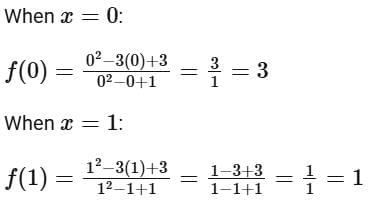
It appears that f (x) achieves values within [1, 3]. To confirm this, we need to solve the quadratic inequality: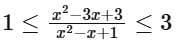
By solving the inequalities, it can be confirmed that the function indeed ranges from 1 to 3 on the interval [0,1]. Hence, we have: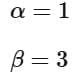
The common ratio of the infinite geometric progression is: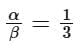
Given the first term a = 64, the sum S of the infinite geometric progression can be given as: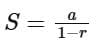
Substituting the values a = 64 and r = 1/3, we get: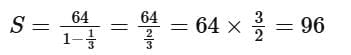
Therefore, the sum of the infinite geometric progression is 96.
Q20. If S = {a ∈ R : |2a - 1| = 3[a] + 2{a}}, where [t] denotes the greatest integer less than or equal to t and {t} represents the fractional part of t , then 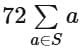 is equal to _________.
is equal to _________.
 View Answer
View Answer 
Ans. 18
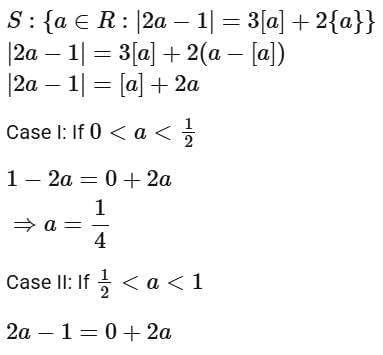
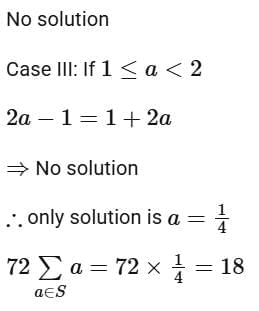
Q21. Consider the function  If the composition of
If the composition of 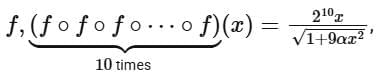 then the value of
then the value of 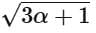 is equal to _______.
is equal to _______.
 View Answer
View Answer 
Ans. 1024
Q22. Let A = {1,2,3, ... , 7} and let P(A) denote the power set of A. If the number of functions f : A → P(A) such that a ∈ f(a), ∀a ∈ A is m", m and n ∈ N and m is least, then m + n is equal to _________.
 View Answer
View Answer 
Ans. 44
2023
Q1. For three positive integers 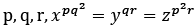 and r = pq + 1 such that 3,3logy x, 3logz y, 7logx z are in A.P. with common difference 1/2. Then r − p − q is equal to
and r = pq + 1 such that 3,3logy x, 3logz y, 7logx z are in A.P. with common difference 1/2. Then r − p − q is equal to
(a) -6
(b) 12
(c) 6
(d) 2
 View Answer
View Answer 
Ans. d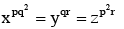
& r = pq + 1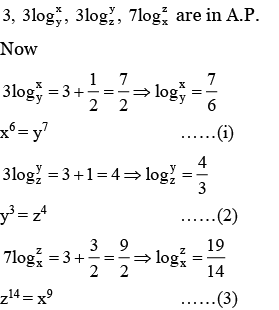
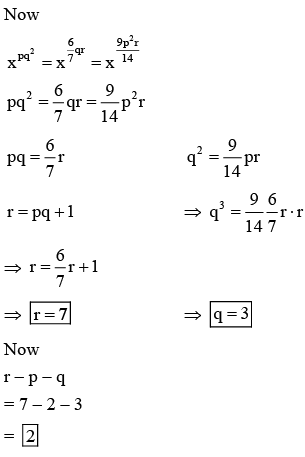
2022
Q1. Let |M| denote the determinant of a square matrix M. Let g: [0, π/2] → R be the function defined by
 View Answer
View Answer 
Solution: 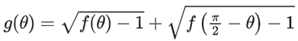
where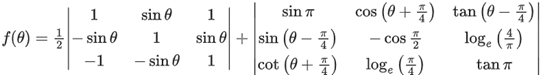
Q2. Let p(x) be a quadratic polynomial whose roots are the maximum and minimum values of the function g(θ), and p(2) = 2 − √2. Then, which of the following is/are TRUE?
(a)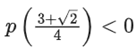
(b)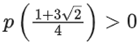
(c)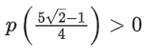
(d)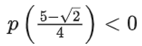
 View Answer
View Answer 
Correct Answe r is Option (a, c)
Q3. The domain of the function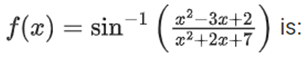
(a) [1, ∞)
(c) [−1, 2]
(c) [−1, ∞)
(d) (−∞, 2]
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: 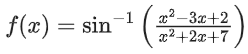
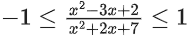
x2 + 2x + 7
5x ≥ − 5
x ≥ −1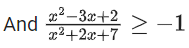
x2 − 3x + 2 ≥ − x2 − 2x − 7
2x2 − x + 9 ≥ 0
x ∈ R
(i) ∩ (ii)
Domain ∈ [−1, ∞)
Q4. The function f(x) = xex(1−x), x ∈ R, is:
(a) increasing in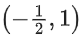
(b) decreasing in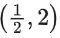
(c) increasing in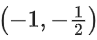
(d) decreasing in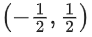
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
f(x) = xex(1−x), x ∈ R
f′(x) = xex(1−x) . (1 − 2x) + ex(1−x)
= ex(1−x)[x − 2x2 + 1]
= −ex(1−x)[2x2 − x − 1]
= −ex(1−x)(2x + 1)(x − 1)
∴ f(x) is increasing in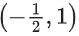 and decreasing in
and decreasing in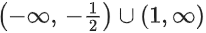
Q5. Let be such that and Let f(x) = ax2 + bx + c be such that f(1) = 3, f(−2) = λ and f(3) = 4. If f(0) + f(1) + f(−2) + f(3) = 14, then λ is equal to:
(a) −4
(b) 13/2
(c) 23/2
(d) 4
 View Answer
View Answer 
Correct Answer is Option (d)
Solution:
f(1) = a + b + c = 3 ..... (i)
f(3) = 9a + 3b + c = 4 .... (ii)
f(0) + f(1) + f(−2) + f(3) = 14
OR c + 3 + (4a − 2b + c) + 4 = 14
OR 4a − 2b + 2c = 7 ..... (iii)
From (i) and (ii) 8a + 2b = 1 ..... (iv)
From (iii) −(2) × (i)
⇒ 2a − 4b = 1 ..... (v)
From (iv) and (v) a = 1/6, b = −1/6 and c = 3
f(−2) = 4a − 2b + c
4/6 + 2/6 + 3 = 4
Q6. Let α, β and γ be three positive real numbers. Let f(x) = αx5 + βx3 + γx, x ∈ R and g : R → R be such that g(f(x)) = x for all x ∈ R. If a1, a2, a3,…, an be in arithmetic progression with mean zero, then the value of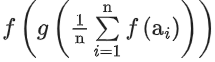 is equal to:
is equal to:
(a) 0
(b) 3
(c) 9
(d) 27
 View Answer
View Answer 
Correct Answer is Option (a)
Solution: 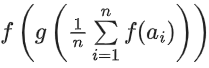

∴ First and last term, second and second last and so on are equal in magnitude but opposite in sign.
f(x) = αx5 + βx3 + γx 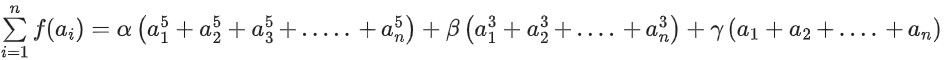 = 0α + 0β + 0γ
= 0α + 0β + 0γ
= 0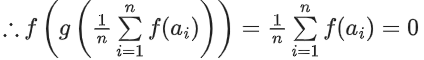
Q7. Considering only the principal values of the inverse trigonometric functions, the domain of the function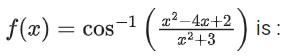
(a) (−∞, 1/4]
(b) 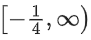
(c) (−1/3, ∞)
(d) (−∞, 1/3]
 View Answer
View Answer 
Correct Answer is Option (b)
Solution: 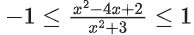
⇒ −x2 − 3 ≤ x2 − 4x + 2 ≤ x2 + 3
⇒ 2x2 − 4x + 5 ≥ 0 & −4x ≤ 1
x ∈ R & x ≥ 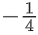
So domain is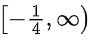
Q8. The domain of the function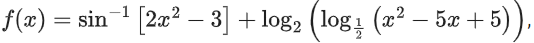 where [t] is the greatest integer function, is:
where [t] is the greatest integer function, is:
(a)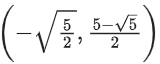
(b)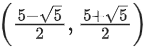
(c)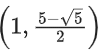
(d)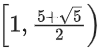
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
−1 ≤ 2x2 − 3 < 2
or 2 ≤ 2x2 < 5
or 1 ≤ x2 < 5/2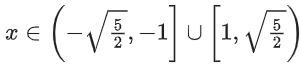
log1/2(x2 − 5x + 5) > 0
0 < x2 − 5x + 5 < 1
x2 − 5x + 5 > 0 & x2 − 5x + 4 < 0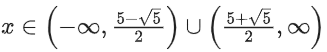
& x ∈ (−∞, 1) ∪ (4, ∞)
Taking intersection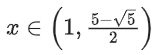
Q9. Let f, g : N − {1} → N be functions defined by f(a) = α, where α is the maximum of the powers of those primes p such that pα divides a, and g(a) = a + 1, for all a ∈ N − {1}. Then, the function f + g is
(a) one-one but not onto
(b) onto but not one-one
(c) both one-one and onto
(d) neither one-one nor onto
 View Answer
View Answer 
Correct Answer is Option (d)
Solution:
f, g : N − {1} → N defined as
f(a) = α, where α is the maximum power of those primes p such that pα divides a.
g(a) = a + 1,
Now,
f(2) = 1, g(2) = 3 ⇒ (f + g)(2) = 4
f(3) = 1, g(3) = 4 ⇒ (f + g)(3) = 5
f(4) = 2, g(4) = 5 ⇒ (f + g)(4) =7
f(5) = 1, g(5) = 6 ⇒ (f + g)(5) = 7
∵ (f + g)(5) = (f + g)(4)
∴ f+g is not one-one
Now, ∵ fmin = 1, gmin = 3
So, there does not exist any x ∈ N − {1} such that (f + g)(x) = 1, 2, 3
∴ f + g is not onto
Q10. If the maximum value of a, for which the function fa(x) = tan−12x − 3ax + 7 is non-decreasing in 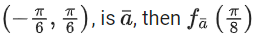 is equal to
is equal to
(a)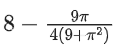
(b)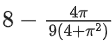
(c)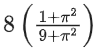
(d)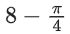
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
fa(x) = tan−12x − 3ax + 7
∵ fa(x) is non-decreasing in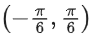
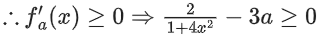
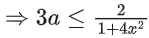
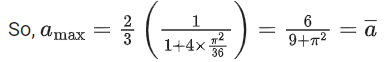
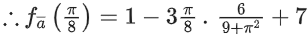
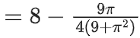
Q11. Let f : R → R be a continuous function such that f(3x) − f(x) = x. If f(8) = 7, then f(14) is equal to:
(a) 4
(b) 10
(c) 11
(d) 16
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
f(3x) − f(x) = x ...... (1)
x → x/3
f(x) − f(x/3) = x/3 ....... (2)
Again x → x/3
f(x/3) − f(x/9) = x/32 ...... (3)
Similarly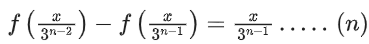
Adding all these and applying n → ∞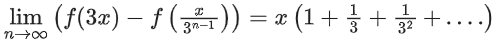
f(3x) − f(0) = 3x/2
Putting x = 8/3
f(8) − f(0) = 4
⇒ f(0) = 3
Putting x = 14/3
f(14) − 3 = 7 ⇒ f(14) = 0
Q12. The number of bijective functions f : {1, 3, 5, 7, …, 99} → {2, 4, 6, 8, …. 100}, such that f(3) ≥ f(9) ≥ f(15) ≥ f(21) ≥ ….. f(99), is ____________.
(a) 50P17
(b) 50P33
(c) 33! × 17!
(d) 50!/2
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
As function is one-one and onto, out of 50 elements of domain set 17 elements are following restriction f(3) > f(9) > f(15) ....... > f(99)
So number of ways = 50C17 . 1 . 33!
= 50!/2
Q13. If the absolute maximum value of the function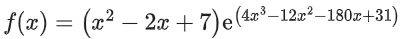 in the interval [−3, 0] is f(α), then:
in the interval [−3, 0] is f(α), then:
(a) α = 0
(b) α = −3
(c) α ∈ (−1, 0)
(d) α ∈ (−3, −1)
 View Answer
View Answer 
Correct Answer is Option (b)
Q14. The total number of functions, f : {1, 2, 3, 4} → {1, 2, 3, 4, 5, 6} such that f(1) + f(2) = f(3), is equal to:
(a) 60
(b) 90
(c) 108
(d) 126
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
Given, f(1) + f(2) = f(3)
It means f(1), f(2) and f(3) are dependent on each other. But there is no condition on f(4), so f(4) can be f(4) = 1, 2, 3, 4, 5, 6.
For f(1), f(2) and we have to find how many functions possible which will satisfy the condition f(1) + f(2) = f(3)
Case 1:
When f(3) = 2 then possible values of f(1) and f(2) which satisfy f(1) + f(2) = f(3) is f(1) = 1 and f(2) = 1.
And f(4) can be = 1, 2, 3, 4, 5, 6
∴ Total possible functions = 1 × 6 = 6
Case 2:
When f(3) = 3 then possible values
(1) f(1) = 1 and f(2) = 2 (2)
f(1) = 2 and f(2) = 1
And f(4) can be = 1, 2, 3, 4, 5, 6.
∴ Total functions = 2 × 6 = 12
Case 3:
When f(3) = 4 then
(1) f(1) = 1 and f(2) = 3
(2) f(1) = 2 and f(2) = 2
(3) f(1) = 3 and f(2) = 1
And f(4) can be = 1, 2, 3, 4, 5, 6
∴ Total functions = 3 × 6 = 18
Case 4:
When f(3) = 5 then
(1) f(1) = 1 and f(4) = 4
(2) f(1) = 2 and f(4) = 3
(3) f(1) = 3 and f(4) = 2
(4) f(1) = 4 and f(4) = 1
And f(4) can be = 1, 2, 3, 4, 5 and 6
∴ Total functions = 4 × 6 = 24
Case 5:
When f(3)=6 then
(1) f(1) = 1 and f(2) = 5
(2) f(1) = 2 and f(2) = 4
(3) f(1) = 3 and f(2) = 3
(4) f(1) = 4 and f(2) = 2
(5) f(1) = 5 and f(2) = 1
And f(4) can be = 1, 2, 3, 4, 5 and 6
∴ Total possible functions = 5 × 6 = 30
∴ Total functions from those 5 cases we get
= 6 + 12 + 18 + 24 + 30 = 90
Q15. Let 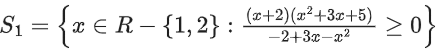 and S2 = {x ∈ R : 32x − 3x+1 − 3x+2 + 27 ≤ 0}. Then, S1 ∪ S2 is equal to:
and S2 = {x ∈ R : 32x − 3x+1 − 3x+2 + 27 ≤ 0}. Then, S1 ∪ S2 is equal to:
(a) (−∞, −2] ∪ (1, 2)
(b) (−∞, −2] ∪ [1, 2]
(c) (−2, 1] ∪ [2, ∞)
(d) (−∞, 2]
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
Given,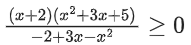
x2 + 3x + 5 is a quadratic equation
a = 1 > 0 and D = (−3)2 − 4 . 1 . 5 = −11 < 0
∴ x2 + 3x + 5 > 0 (always)
So, we can ignore this quadratic term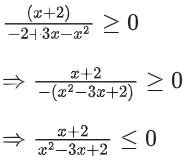
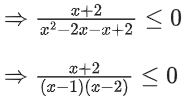
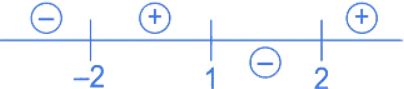
∴ x ∈ (−α, −2] ∪ (1, 2)
∴ S1 = (−α, −2] ∪ (1, 2)
Now,
32x − 3x+1 − 3x+2 + 27 ≤ 0
⇒ (3x)2 − 3 . 3x − 32 . 3x + 27 ≤ 0
Let 3x = t
⇒ t2 − 3 . t − 32 . t + 27 ≤ 0
⇒ t(t − 3) − 9(t − 3) ≤ 0
⇒ (t − 3)(t − 9) ≤ 0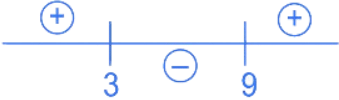
∴ 3 ≤ t ≤ 9
⇒ 31 ≤ 3x ≤ 32
⇒ 1 ≤ x ≤ 2
∴ x ∈ [1, 2]
∴ S2 = [1, 2]
∴ S1 ∪ S2 = (−α, 2] ∪ (1, 2) ∪ [1, 2]
Q16. The domain of the function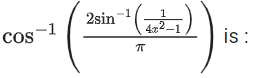
(a)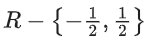
(b) (−∞, −1] ∪ [1, ∞) ∪ {0}
(c)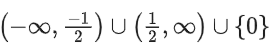
(d)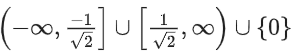
 View Answer
View Answer 
Correct Answer is Option (d)
Solution: 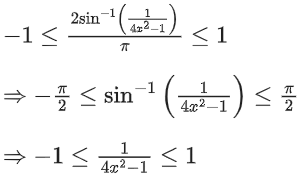
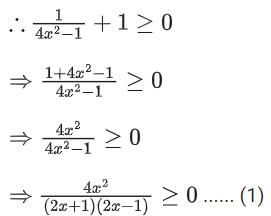
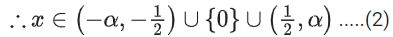
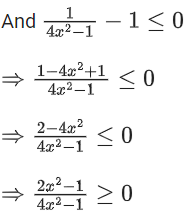
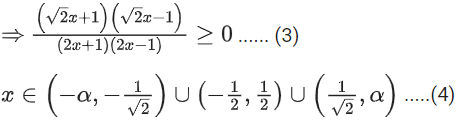
From (3) and (4), we get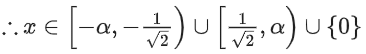
Q17. Let a function f : N → N be defined by 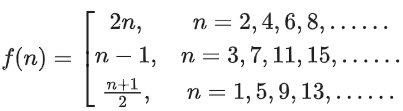
then, f is
(a) one-one but not onto
(b) onto but not one-one
(c) neither one-one nor onto
(d) one-one and onto
 View Answer
View Answer 
Correct Answer is Option (d)
Solution:
When n = 1, 5, 9, 13 then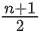 will give all odd numbers.
will give all odd numbers.
When n = 3, 7, 11, 15 .....
n − 1 will be even but not divisible by 4
When n = 2, 4, 6, 8 .....
Then 2n will give all multiples of 4
So range will be N.
And no two values of n give same y, so function is one-one and onto.
Q18. Let f : R → R be defined as f (x) = x − 1 and g : R − {1, −1} → R be defined as g(x)=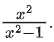 Then the function fog is:
Then the function fog is:
(a) one-one but not onto
(b) onto but not one-one
(c) both one-one and onto
(d) neither one-one nor onto
 View Answer
View Answer 
Correct Answer is Option (d)
Solution:
f : R → R defined as
f(x) = x − 1 and g : R → {1, −1} → R, g(x) =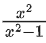
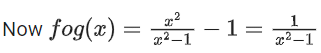
∴ Domain of fog(x)=R−{−1,1}
And range of fog(x) = (−∞, −1] ∪ (0, ∞)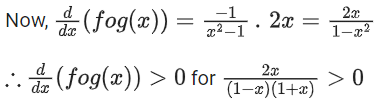
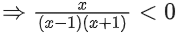
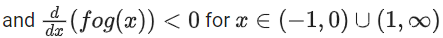
∴ fog(x) is neither one-one nor onto.
Q19. Let f(x) = 2cos−1x + 4cot−1x − 3x2 − 2x + 10, x ∈ [−1, 1]. If [a, b] is the range of the function f, then 4a − b is equal to:
(a) 11
(b) 11 − π
(c) 11 + π
(d) 15 − π
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
f(x) = 2cos−1x + 4cot−1x − 3x2 − 2x + 10 ∀ x ∈ [−1, 1]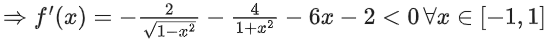
So f(x) is decreasing function and range of f(x) is [f(1), f(−1)], which is [π + 5, 5π + 9]
Now 4a − b = 4(π + 5) − (5π + 9)
= 11 − π
Q20. Let f(x) =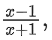 , x ∈ R − {0, −1, 1}. If fn+1(x) = f(fn(x)) for all n ∈ N, then f6(6) + f7(7) is equal to:
, x ∈ R − {0, −1, 1}. If fn+1(x) = f(fn(x)) for all n ∈ N, then f6(6) + f7(7) is equal to:
(a) 7/6
(b)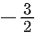
(c) 7/12
(d)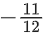
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
Given,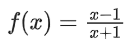
Also given, fn+1(x) = f(fn(x)) ..... (1)
∴ For n = 1
f1+1(x) = f(f1(x))
⇒ f2(x) = f(f(x))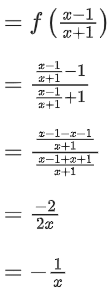
From equation (1), when n = 2
f2+1(x) = f(f2(x))
⇒ f3(x) = f(f2(x))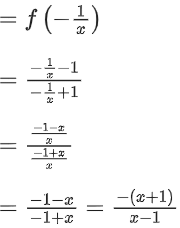
Similarly,
f4(x) = f(f3(x))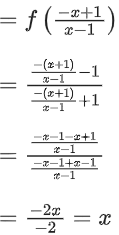
∴ f5(x) = f(f4(x))
= f(x)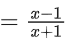
f6(x) = f(f5(x))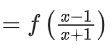
= −1x (Already calculated earlier)
f7(x) = f(f6(x))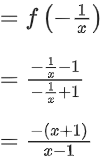
∴ f6(6) =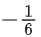
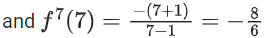
So, f6(6) + f7(7)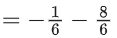
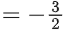
Q21. Let f : R → R and g : R → R be two functions defined by f(x) = loge(x2 + 1) − e−x + 1 and 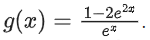 Then, for which of the following range of α, the inequality
Then, for which of the following range of α, the inequality 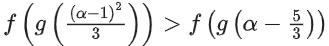 holds?
holds?
(a) (2, 3)
(b) (−2, −1)
(c) (1, 2)
(d) (−1, 1)
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
f(x) = loge(x2 + 1) − e−x + 1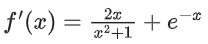
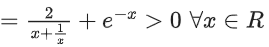
g(x) = e−x − 2ex
g′(x)−−e−x − 2ex < 0 ∀x ∈ R
⇒ f(x) is increasing and g(x) is decreasing function.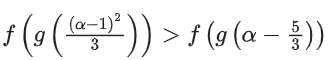
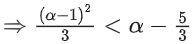
= α2 − 5α + 6 < 0
= (α − 2)(α − 3) < 0
= α ∈ (2, 3)
Q22. Let f(x) be a polynomial function such that f(x) + f′(x) + f″(x) = x5 + 64. Then, the value of 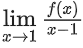 is equal to:
is equal to:
(a) −15
(b) −60
(c) 60
(d) 15
 View Answer
View Answer 
Correct Answer is Option (a)
Solution: 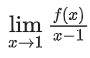
f(x) + f′(x) + f″(x) = x5 + 64
Let f(x) = x5 + ax4 + bx3 + cx2 + dx + e
f′(x) = 5x4 + 4ax3 + 3bx2 + 2cx + d
f″(x) = 20x3 + 12ax2 + 6bx + 2c
x5(a + 5)x4 + (b + 4a + 20)x3 + (c + 3b + 12a)x2 + (d + 2c + 6b)x + e + d + 2c = x5 + 64
⇒ a + 5 = 0
b + 4a + 20 = 0
c + 3b + 12a = 0
d + 2c + 6b = 0
e + d + 2c = 64
∴ a = −5, b = 0, c = 60, d = −120, e = 64
∴ f(x) = x5 − 5x4 + 60x2 − 120x + 64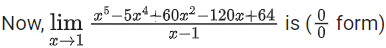
By L' Hospital rule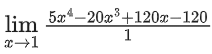
= -15
Q23. Let f : R → R be defined as f(x) = x3 + x − 5. If g(x) is a function such that f(g(x)) = x, ∀′x′ ∈ R, then g'(63) is equal to ______________.
(a) 1/49
(b) 3/49
(c) 43/49
(d) 91/49
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
f(x) = 3x2 + 1
f'(x) is bijective function
and f(g(x)) = x ⇒ g(x) is inverse of f(x)
g(f(x)) = x
g′(f(x)) . f′(x) = 1
g′(f(x)) =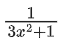
Put x = 4 we get
g′(63) = 1/49
Q24. Let f : N → R be a function such that f(x + y) = 2f(x)f(y) for natural numbers x and y. If f(1) = 2, then the value of α for which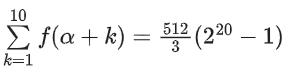 holds, is:
holds, is:
(a) 2
(b) 3
(c) 4
(d) 6
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
Given,
f(x + y) = 2f(x)f(y)
and f(1) = 2
For x = 1 and y = 1,
f(1 + 1) = 2f(1)f(1)
⇒ f(2) = 2(f(1))2 = 2(2)2 = 23
For x = 1, y = 2,
f(1 + 2) = 2f(1)y(2)
⇒ f(3) = 2 . 2 . 23 = 25
For x = 1, y = 3,
f(1 + 3) = 2f(1)f(3)
⇒ f(4) = 2 . 2 . 25 = 27
For x = 1, y = 4,
f(1 + 4) = 2f(1)f(4)
⇒ f(5) = 2 . 2 . 27 = 29 ..... (1)
Also given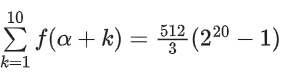
⇒ f(α + 1) + f(α + 2) + f(α + 3) + ... + f(α + 10) = 512/3(220 − 1)
⇒ f(α + 1) + f(α + 2) + f(α + 3) + .... + f(α + 10) =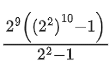
This represent a G.P with first term = 29 and common ratio = 22
∴ First term = f(α + 1) = 29 ..... (2)
From equation (1), f(5) = 29
∴ From (1) and (2), we get f(α + 1) = 29 = f(5)
⇒ f(α + 1) = f(5)
⇒ f(α + 1) = f(4 + 1)
Comparing both sides we get,
α = 4
Q25. The domain of the function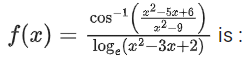
(a) (−∞, 1) ∪ (2, ∞)
(b) (2, ∞)
(c)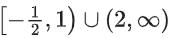
(d)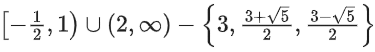
 View Answer
View Answer 
Correct Answer is Option (d)
Solution: 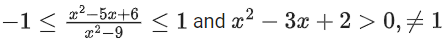
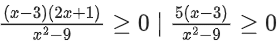
The solution to this inequality is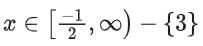
for x2 − 3x + 2 > 0 and ≠ 1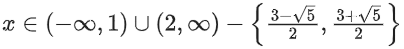
Combining the two solution sets (taking intersection)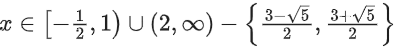
Q26. The sum of absolute maximum and absolute minimum values of the function f(x) = |2x2 + 3x − 2| + sinx cosx in the interval [0, 1] is:
(a)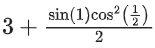
(b)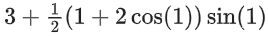
(c)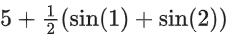
(d)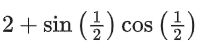
 View Answer
View Answer 
Correct Answer is Option b
Solution: 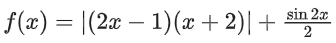
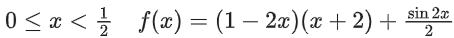
f′(x) = −4x − 3 + cos2x < 0
For x ≥ 1/2: f′(x) = 4x + 3 + cos2x > 0
So, minima occurs at x = 1/2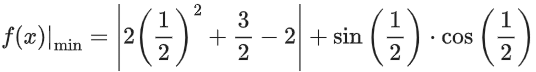
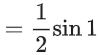
So, maxima is possible at x = 0 or x = 1
Now checking for x = 0 and x = 1, we can see it attains its maximum value at x = 1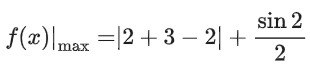
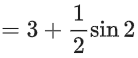
Sum of absolute maximum and minimum value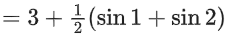
Q27. For the function f(x) = 4loge(x − 1) − 2x2 + 4x + 5, x > 1, which one of the following is NOT correct?
(a) f is increasing in (1, 2) and decreasing in (2, ∞)
(b) f(x) = −1 has exactly two solutions
(c) f′(e) − f″(2) < 0
(d) f(x) = 0 has a root in the interval (e, e + 1)
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
f(x) = 4loge(x − 1) − 2x2 + 4x + 5, x > 1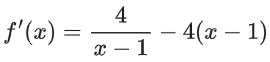
For 1 < x < 2 ⇒ f′(x) > 0
For x > 2 ⇒ f′(x) < 0 (option A is correct)
f(x) = −1 has two solution (option B is correct)
f(e) > 0
f(e + 1) < 0
f(e) ⋅ f(e + 1) < 0 (option D is correct)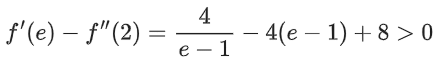
(option C is incorrect)
Q28. For p, q ∈ R, consider the real valued function f(x) = (x − p)2 − q, x ∈ R and q > 0. Let a1, a2, a3 and a4 be in an arithmetic progression with mean p and positive common difference. If |f(ai)| = 500 for all i = 1, 2, 3, 4, then the absolute difference between the roots of f(x) = 0 is ___________.
 View Answer
View Answer 
Solution:
∵ a1, a2, a3, a4
∴ a2 = p − 3d, a2 = p − d, a3 = p + d and a4 = p + 3d
Where d > 0
∵ |f(ai)| = 500
⇒ |9d2 − q| = 500
and |d2 − q| = 500 ..... (i)
either 9d2 − q = d2 − q
⇒ d = 0 not acceptable
∴ 9d2 − q = q − d2
∴ 5d2 − q = 0 ..... (ii)
Roots of f(x) = 0 are p + √q and p − √q
∴ absolute difference between roots = |2√q| = 50
Q29. The number of functions f, from the set A = {x ∈ N : x2 − 10x + 9 ≤ 0} to the set B = {n2 : n ∈ N} such that f(x) ≤ (x − 3)2 + 1, for every x ∈ A, is ___________.
 View Answer
View Answer 
Solution:
A = {x ∈ N, x2 − 10x + 9 ≤ 0}
= {1, 2, 3, ...., 9}
B = {1, 4, 9, 16, .....}
f(x) ≤ (x − 3)2 + 1
f(1) ≤ 5, f(2) ≤ 2, .......... f(9) ≤ 37
x = 1 has 2 choices
x = 2 has 1 choice
x = 3 has 1 choice
x = 4 has 1 choice
x = 5 has 2 choices
x = 6 has 3 choices
x = 7 has 4 choices
x = 8 has 5 choices
x = 9 has 6 choices
∴ Total functions = 2 x 1 x 1 x 1 x 2 x 3 x 4 x 5 x 6 = 1140
Q30. Let f(x) = 2x2 − x − 1 and S = {n ∈ Z : |f(n)| ≤ 800}. Then, the value of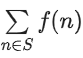 is equal to ___________.
is equal to ___________.
 View Answer
View Answer 
Solution:
∵ |f(n)| ≤ 800
⇒ −800 ≤ 2n2 − n − 1 ≤ 800
⇒ 2n2 − n − 801 ≤ 0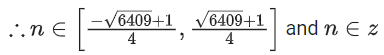
∴ n = −19, −18, −17, .........., 19, 20.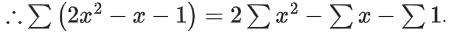
= 2 . 2 . (12 + 22 + ... + 192) + 2 . 202 − 20 − 40
= 10620
Q31. The sum of the maximum and minimum values of the function f(x) = |5x − 7| + [x2 + 2x] in the interval [5/4, 2], where [t] is the greatest integer ≤ t, is ______________.
 View Answer
View Answer 
Solution:
f(x) = |5x − 7| + [x2 + 2x]
= |5x − 7| + [(x + 1)2] − 1
Critical points of
f(x) = 7/5, √5 − 1, √6 − 1, √7 − 1, √8 − 1, 2
∴ Maximum or minimum value of f(x) occur at critical points or boundary points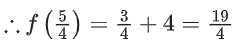
f(7/5) = 0 + 4 = 4
as both |5x − 7| and x2 + 2x are increasing in nature after x = 7/5
∴ f(2) = 3 + 8 = 11
∴ f(7/5)min = 4 and f(2)max = 11
Sum is 4 + 11 = 15
Q32. Let f(x) be a quadratic polynomial with leading coefficient 1 such that f(0) = p, p ≠ 0, and f(1) = 13. If the equations f(x) = 0 and f ∘ f ∘ f ∘ f(x) = 0 have a common real root, then f(−3) is equal to ________________.
 View Answer
View Answer 
Solution:
Let f(x) = (x − α)(x − β)
It is given that f(0) = p ⇒ αβ = p
and f(1) = 1/3 ⇒ (1 − α)(1 − β) = 1/3
Now, let us assume that, α is the common root of f(x) = 0 and f ∘ f ∘ f ∘ f(x) = 0
f ∘ f ∘ f ∘ f(x) = 0
⇒ f ∘ f ∘ f(0) = 0
⇒ f ∘ f(p) = 0
So, f(p) is either α or β.
(p − α)(p − β) = α
(αβ − α)(αβ − β) = α ⇒ (β − 1)(α − 1)β = 1 (∵ α ≠ 0)
So, β = 3
(1 − α)(1 − 3) = 1/3
α = 7/6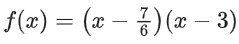
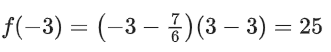
Q33. Let f(x) and g(x) be two real polynomials of degree 2 and 1 respectively. If f(g(x)) = 8x2 − 2x and g(f(x)) = 4x2 + 6x + 1, then the value of f(2) + g(2) is _________.
 View Answer
View Answer 
Ans. 18
Q34. Let c, k ∈ R. If f(x) = (c + 1)x2 + (1 − c2)x + 2k and f(x + y) = f(x) + f(y) − xy, for all x, y ∈ R, then the value of |2(f(1) + f(2) + f(3) + ...... + f(20))| is equal to ____________.
 View Answer
View Answer 
Solution:
f(x) is polynomial
Put y = 1/x in given functional equation we get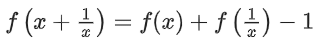
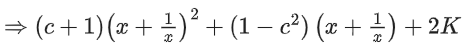
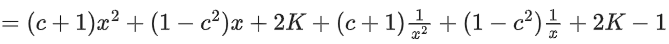
⇒ 2(c + 1) = 2K − 1 ..... (1)
and put x = y = 0 we get
f(0) = 2 + f(0) − 0 ⇒ f(0) = 0 ⇒ k = 0
∴ k = 0 and 2c = −3 ⇒ c = −3/2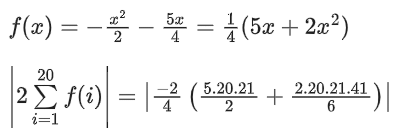
Q35. Let [t] denote the greatest integer ≤ t and {t} denote the fractional part of t. The integral value of α for which the left hand limit of the function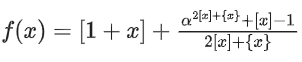 at x = 0 is equal to
at x = 0 is equal to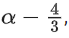 is _____________.
is _____________.
 View Answer
View Answer 
Solution: 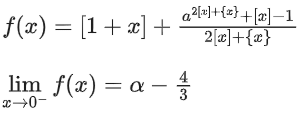
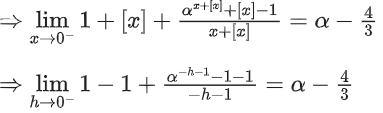
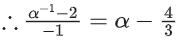
⇒ 3α2 − 10α + 3 = 0
∴ α = 3 or 1/3
∵ α in integer, hence α = 3
Q36. Let S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.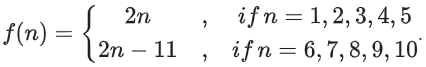
Let g : S → S be a function such that 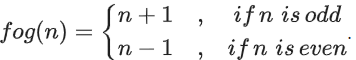
Then g(10)g(1) + g(2) + g(3) + g(4) + g(5)) is equal to _____________.
 View Answer
View Answer 
Solution: 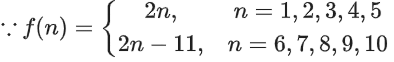
∴ f(1) = 2, f(2) = 4, ......, f(5) = 10
and f(6) = 1, f(7) = 3, f(8) = 5, ......, f(10) = 9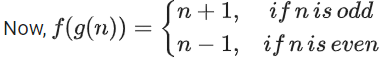
∴ f(g(10)) = 9 ⇒ g(10) = 10
f(g(1)) = 2 ⇒ g(1) = 1
f(g(2)) = 1 ⇒ g(2) = 6
f(g(3)) = 4 ⇒ g(3) = 2
f(g(4)) = 3 ⇒ g(4) = 7
f(g(5)) = 6 ⇒ g(5) = 3
∴ g(10)g(1) + g(2) + g(3) + g(4) + g(5)) = 190
Q37. Let f : R → R be a function defined by 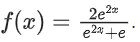 Then
Then 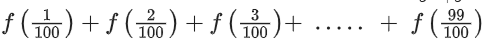 is equal to ______________.
is equal to ______________.
 View Answer
View Answer 
Solution: 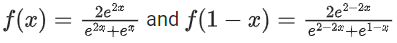
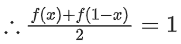
i.e. f(x) + f(1 − x) = 2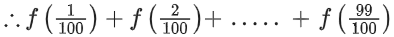
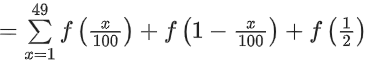
= 49 x 2 + 1 = 99
Q38. Let f : R → R satisfy f(x + y) = 2xf(y) + 4yf(x), ∀x, y ∈ R. If f(2) = 3, then 14. f′(4)/f′(2) is equal to ____________.
 View Answer
View Answer 
Solution:
∵ f(x + y) = 2xf(y) + 4yf(x) ....... (1)
Now, f(y + x)2yf(x) + 4xf(y) ...... (2)
∴ 2xf(y) + 4yf(x) = 2yf(x) + 4xf(y)
(4y − 2y)f(x) = (4x − 2x)f(y)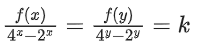
∴ f(x) = k(4x − 2x)
∵ f(2) = 3 then k = 1/4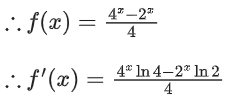
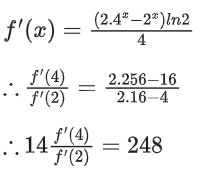
Q39. Let f : R → R be a function defined by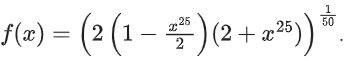 If the function g(x) = f(f(f(x)) + f(f(x)), then the greatest integer less than or equal to g(1) is ____________.
If the function g(x) = f(f(f(x)) + f(f(x)), then the greatest integer less than or equal to g(1) is ____________.
 View Answer
View Answer 
Solution:
Given,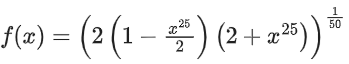
and g(x) = f(f(f(x))) + f(f(x))
∴ g(1) = f(f(f(1))) + f(f(1))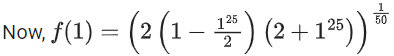
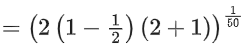
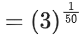
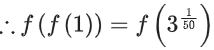
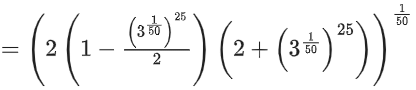
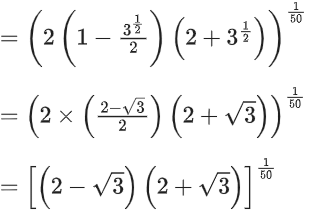
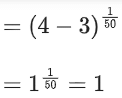
Now, f(f(f(1))) = f(1) = 31/50
∴ g(1) = f(f(f(1))) + f(f(1)) = 31/50 + 1
Now, greatest integer less than or equal to g(1)
= [g(1)]
= [31/50 + 1]
= [31/50] + [1]
= [1.02] + 1
= 1 + 1 = 2
Q40. The number of points where the function f(x)=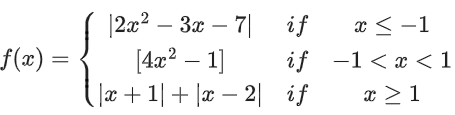
[t] denotes the greatest integer ≤ t, is discontinuous is _____________.
 View Answer
View Answer 
Solution:
∵ f(−1) = 2 and f(1) = 3
For x ∈ (−1, 1), (4x2 − 1) ∈ [−1, 3)
hence f(x) will be discontinuous at x = 1 and also
whenever 4x2 − 1 = 0, 1 or 2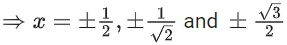
So there are total 7 points of discontinuity.
Q41. The number of one-one functions f : {a, b, c, d} → {0, 1, 2, ......, 10} such that 2f(a) − f(b) + 3f(c) + f(d) = 0 is ___________.
 View Answer
View Answer 
Solution:
Given one-one function
f : {a, b, c, d} → {0, 1, 2, .... 10}
and 2f(a) − f(b) + 3f(c) + f(d) = 0
⇒ 3f(c) + 2f(a) + f(d) = f(b)
Case I:
(1) Now let f(c) = 0 and f(a) = 1 then
3 × 0 + 2 × 1 + f(d) = f(b)
⇒ 2 + f(d) = f(b)
Now possible value of f(d) = 2, 3, 4, 5, 6, 7, and 8.
f(d) can't be 9 and 10 as if f(d) = 9 or 10 then f(b) = 2 + 9 = 11 or f(b) = 2 + 10 = 12, which is not possible as here any function's maximum value can be 10.
∴ Total possible functions when f(c) = 0 and f(a) = 1 are = 7
(2) When f(c) = 0 and f(a) = 2 then
3 × 0 + 2 × 2 + f(d) = f(b)
⇒ 4 + f(d) = f(b)
∴ possible value of f(d) = 1, 3, 4, 5, 6
∴ Total possible functions in this case = 5
(3) When f(c) = 0 and f(a) = 3 then
3 × 0 + 2 × 3 + f(d) = f(b)
⇒ 6 + f(d) = f(b)
∴ Possible value of f(d) = 1, 2, 4
∴ Total possible functions in this case = 3
(4) When f(c) = 0 and f(a) = 4 then
3 × 0 + 2 × 4 + f(d) = f(b)
⇒ 8 + f(d) = f(b)
∴ Possible value of f(d) = 1, 2
∴ Total possible functions in this case = 2
(5) When f(c) = 0 and f(a) = 5 then
3 × 0 + 2 × 5 + f(d) = f(b)
⇒ 10 + f(d) = f(b)
Possible value of f(d) can be 0 but f(c) is already zero. So, no value to f(d) can satisfy.
∴ No function is possible in this case.
∴ Total possible functions when f(c) = 0 and f(a) = 1, 2, 3 and 4 are = 7 + 5 + 3 + 2 = 17
Case II:
(1) When f(c) = 1 and f(a) = 0 then
3 × 1 + 2 × 0 + f(d) = f(b)
⇒ 3 + f(d) = f(b)
∴ Possible value of f(d) = 2, 3, 4, 5, 6, 7
∴ Total possible functions in this case = 6
(2) When f(c) = 1 and f(a) = 2 then
3 × 1 + 2 × 2 + f(d) = f(b)
⇒ 7 + f(d) = f(b)
∴ Possible value of f(d) = 0, 3
∴ Total possible functions in this case = 2
(3) When f(c) = 1 and f(a) = 3 then
3 × 1 + 2 × 3 + f(d) = f(b)
⇒9 + f(d) = f(b)
∴ Possible value of f(d) = 0
∴ Total possible functions in this case = 1
∴ Total possible functions when f(c) = 1 and f(a) = 0, 2 and 3 are
= 6 + 2 + 1 = 9
Case III:
(1) When f(c) = 2 and f(a) = 0 then
3 × 2 + 2 × 0 + f(d) = f(b)
⇒ 6 + f(d) = f(b)
∴ Possible values of f(d) = 1, 3, 4
∴ Total possible functions in this case = 3
(2) When f(c) = 2 and f(a) = 1 then,
3 × 2 + 2 × 1 + f(d) = f(b)
⇒ 8 + f(d) = f(b)
∴ Possible values of f(d) = 0
∴ Total possible function in this case = 1
∴ Total possible functions when f(c) = 2 and f(a) = 0, 1 are = 3 + 1 = 4
Case IV:
(1) When f(c) = 3 and f(a) = 0 then
3 × 3 + 2 × 0 + f(d) = f(b)
⇒ 9 + f(d) = f(b)
∴ Possible values of f(d) = 1
∴ Total one-one functions from four cases
= 17 + 9 + 4 + 1 = 31
2021
Q1. The number of 4-digit numbers which are neither multiple of 7 nor multiple of 3 is ____________.
 View Answer
View Answer 
Solution:
A = 4-digit numbers divisible by 3
A = 1002, 1005, ....., 9999.
9999 = 1002 + (n − 1)3
⇒ (n − 1)3 = 8997 ⇒ n = 3000
B = 4-digit numbers divisible by 7
B = 1001, 1008, ......., 9996
⇒ 9996 = 1001 + (n − 1)7
⇒ n = 1286
A ∩ B = 1008, 1029, ....., 9996
9996 = 1008 + (n − 1)21
⇒ n = 429
So, no divisible by either 3 or 7
= 3000 + 1286 − 429 = 3857
total 4-digits numbers = 9000
required numbers = 9000 − 3857 = 5143
Q2. If A = {x ∈ R : |x − 2| > 1},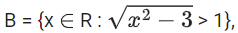
C = {x ∈ R : |x − 4| ≥ 2} and Z is the set of all integers, then the number of subsets of the
set (A ∩ B ∩ C)c ∩ Z is ________________.
 View Answer
View Answer 
Solution:
A = (−∞, 1) ∪ (3, ∞)
B = (−∞, −2) ∪ (2, ∞)
C = (−∞, 2] ∪ [6, ∞)
So, A ∩ B ∩ C = (−∞, −2) ∪ [6, ∞)
z ∩ (A ∩ B ∩ C)' = {−2, −1, 0, −1, 2, 3, 4, 5}
Hence, no. of its subsets = 28 = 256.
Q3. Let S = {1, 2, 3, 4, 5, 6, 7}. Then the number of possible functions f : S → S
such that f(m . n) = f(m) . f(n) for every m, n ∈ S and m . n ∈ S is equal to _____________.
 View Answer
View Answer 
Solution:
F(mn) = f(m) . f(n)
Put m = 1 f(n) = f(1) . f(n) ⇒ f(1) = 1
Put m = n = 2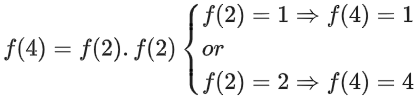
Put m = 2, n = 3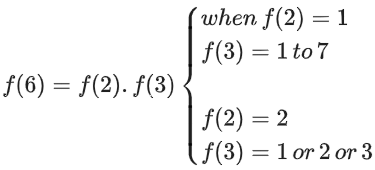
f(5), f(7) can take any value
Total = (1 × 1 × 7 × 1 × 7 × 1 × 7) + (1 × 1 × 3 × 1 × 7 × 1 × 7)
= 490
Q4. Let A = {n ∈ N | n2 ≤ n + 10,000}, B = {3k + 1 | k∈ N} an dC = {2k | k ∈ N}, then the sum of all the elements of the set A ∩(B − C) is equal to _____________.
 View Answer
View Answer 
Solution:
B − C ≡ {7, 13, 19, ......, 97, .......}
Now, n2 − n ≤ 100 × 100
⇒ n(n − 1) ≤ 100 × 100
⇒ A = {1, 2, ......., 100}.
So, A∩(B − C) = {7, 13, 19, ......., 97}
Hence, sum =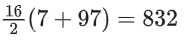
Q5. Let A = {0, 1, 2, 3, 4, 5, 6, 7}. Then the number of bijective functions f : A → A such that f(1) + f(2) = 3 − f(3) is equal to
 View Answer
View Answer 
Solution:
f(1) + f(2) = 3 − f(3)
⇒ f(1) + f(2) = 3 + f(3) = 3
The only possibility is: 0 + 1 + 2 = 3
⇒ Elements 1, 2, 3 in the domain can be mapped with 0, 1, 2 only.
So number of bijective functions.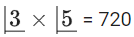
Q6. If f(x) and g(x) are two polynomials such that the polynomial P(x) = f(x3) + x g(x3) is divisible by x2 + x + 1, then P(1) is equal to ___________.
 View Answer
View Answer 
Solution:
Given, p(x) = f(x3) + xg(x3)
We know, x2 + x + 1 = (x − ω) (x − ω2)
Given, p(x) is divisible by x2 + x + 1. So, roots of p(x) is ω and ω2.
As root satisfy the equation,
So, put x = ω
p(ω) = f(ω3) + ωg(ω3) = 0
= f(1) + ωg(1) = 0 [ω3 = 1]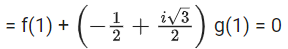
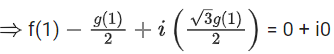
Comparing both sides, we get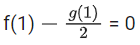
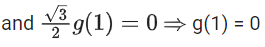
So, f(1) = 0
Now, p(1) = f(1) + 1 . g(1) = 0 + 0 = 0
Q7. If a + α = 1, b + β = 2 and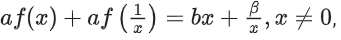 then the value of the expression
then the value of the expression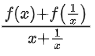 is __________.
is __________.
 View Answer
View Answer 
Solution: 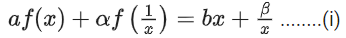
Replace x with 1/x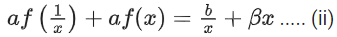
(i) + (ii)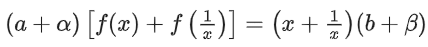
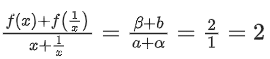
Q8. Let A = {n∈N: n is a 3-digit number}
B = {9k + 2: k ∈ N}
and C = {9k + l: k ∈ N} for some l(0 < l < 9)
If the sum of all the elements of the set A ∩ (B ∪ C) is 274 × 400, then l is equal to ________.
 View Answer
View Answer 
Solution:
3 digit number of the form 9K + 2 are {101, 109, .............992}
⇒ Sum equal to 100/2 (1093) = s1 = 54650
274 × 400 = s1 + s2
274 × 400 = 100/2 [101 + 992] + s2
274 × 400 = 50 × 1093 + s2
s2 = 109600 − 54650
s2 = 54950
s2 = 54950 = 100/2[(99 + l) + (990 + l)]
1099 = 2l + 1089
l = 5
Q9. The range of the function,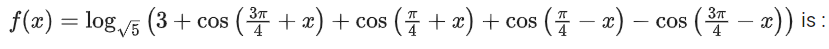
(a) (0, √5)
(b) [-2, 2]
(c)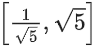
(d) [0, 2]
 View Answer
View Answer 
Correct Answer is Option (d)
Solution: 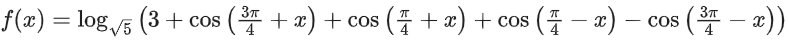
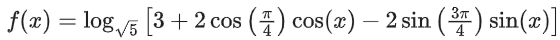
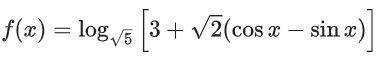
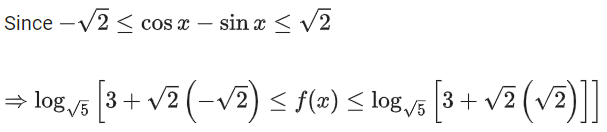
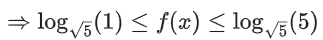
So, Range of f(x) is [0, 2]
Q10. Let f : N → N be a function such that f(m + n) = f(m) + f(n) for every m, n ∈ N. If f(6) = 18, then f(2) . f(3) is equal to:
(a) 6
(b) 54
(c) 18
(d) 36
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
f(m + n) = f(m) + f(n)
Put m = 1, n = 1
f(2) = 2f(1)
Put m = 2, n = 1
f(3) = f(2) + f(1) = 3f(1)
Put m = 3, n = 3
f(6) = 2f(3) ⇒ f(3) = 9
⇒ f(1) = 3, f(2) = 6
f(2) . f(3) = 6 × 9 = 54
Q11. The domain of the function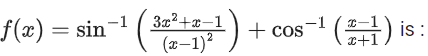
(a)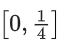
(b)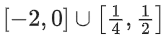
(c)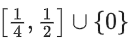
(d)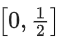
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: 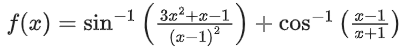
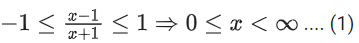
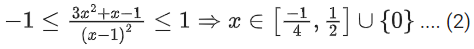
(1) & (2)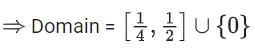
Q12. Which of the following is not correct for relation R on the set of real numbers?
(a) (x, y) ∈ R ⇔ 0 < |x| − |y| ≤ 1 is neither transitive nor symmetric.
(b) (x, y) ∈ R ⇔ 0 < |x − y| ≤ 1 is symmetric and transitive.
(c) (x, y) ∈ R ⇔ |x| − |y| ≤ 1 is reflexive but not symmetric.
(d) (x, y) ∈ R ⇔ |x − y| ≤ 1 is reflexive and symmetric.
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
Note that (a, b) and (b, c) satisfy 0 < |x − y| ≤ 1 but (a, c) does not satisfy it so 0 ≤ |x − y| ≤ 1 is symmetric but not transitive.
For example,
x = 0.2, y = 0.9, z = 1.5
0 ≤ |x – y| = 0.7 ≤ 1
0 ≤ |y – z| = 0.6 ≤ 1
But |x – z| = 1.3 > 1
So, (b) is correct.
Q13. The domain of the function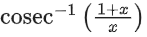 is:
is:
(a)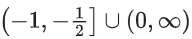
(b)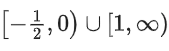
(c)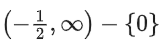
(d)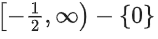
 View Answer
View Answer 
Correct Answer is Option (d)
Solution: 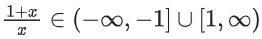
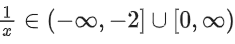
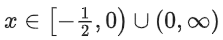
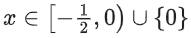
Q14. Let [t] denote the greatest integer less than or equal to t. Let
f(x) = x − [x], g(x) = 1 − x + [x], and h(x) = min{f(x), g(x)}, x ∈ [−2, 2]. Then h is:
(a) A continuous in [−2, 2] but not differentiable at more than four points in (−2, 2)
(b) not continuous at exactly three points in [−2, 2]
(c) continuous in [−2, 2] but not differentiable at exactly three points in (−2, 2)
(d) not continuous at exactly four points in [−2, 2]
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
min{x − [x], 1 − x + [x]}
h(x) = min{x − [x], 1 − [x − [x])}
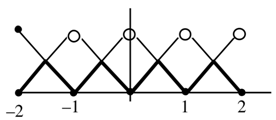
Q15. Out of all patients in a hospital 89% are found to be suffering from heart ailment and 98% are suffering from lungs infection. If K% of them are suffering from both ailments, then K can not belong to the set:
(a) {80, 83, 86, 89}
(b) {84, 86, 88, 90}
(c) {79, 81, 83, 85}
(d) {84, 87, 90, 93}
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
n(A ∪ B) ≥ n(A) + n(B) − n(A ∩ B)
100 ≥ 89 + 98 − n(A ∪ B)
n(A ∩ B) ≥ 87
87 ≤ n(A ∩ B) ≤ 89
Q16. Let N be the set of natural numbers and a relation R on N be defined by R = {(x, y) ∈ N × N : x3 − 3x2y − xy2 + 3y3 = 0}. Then the relation R is:
(a) symmetric but neither reflexive nor transitive
(b) reflexive but neither symmetric nor transitive
(c) reflexive and symmetric, but not transitive
(d) an equivalence relation
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
x3 − 3x2y − xy2 + 3y3 = 0
⇒ x(x2 − y2) − 3y(x2 − y2) = 0
⇒ (x − 3y)(x − y)(x + y) = 0
Now, x = y ∀(x, y) ∈N × N so reflexive but not symmetric & transitive.
See, (3, 1) satisfies but (1, 3) does not. Also (3, 1) & (1, −1) satisfies but (3, −1) does not.
Q17. Let f : R → R be defined as f(x + y) + f(x − y) = 2f(x)f(y), f(1/2) = −1. Then, the value of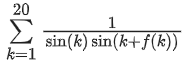 is equal to:
is equal to:
(a) cosec2(21) cos(20) cos(2)
(b) sec2(1) sec(21) cos(20)
(c) cosec2(1) cosec(21) sin(20)
(d) sec2(21) sin(20) sin(2)
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
f(x) = cosλx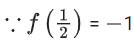
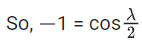
⇒ λ = 2π
Thus f(x) = cos2πx
Now k is natural number
Thus f(k) = 1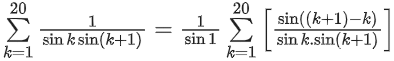
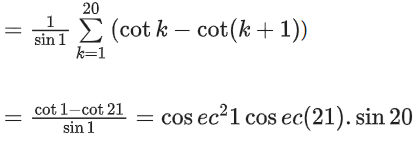
Q18. Consider function f : A → B and g : B → C (A, B, C ⊆ R) such that (gof)−1 exists, then:
(a) f and g both are one-one
(b) f and g both are onto
(c) f is one-one and g is onto
(d) f is onto and g is one-one
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
∴ (gof)−1 exist ⇒ gof is bijective
⇒ 'f' must be one-one and 'g' must be ONTO.
Q19. If [x] be the greatest integer less than or equal to x, then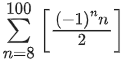 is equal to:
is equal to:
(a) 0
(b) 4
(c) -2
(d) 2
 View Answer
View Answer 
Correct Answer is Option (b)
Solution: 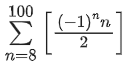
= [4] + [-4.5] + [5] + [-5.5] + [6] +..... + [-49.5] + [50]
= 4 - 5 + 5 - 6 + 6 ......-50 + 50
= 4
Q20. Let g : N → N be defined as
g(3n + 1) = 3n + 2,
g(3n + 2) = 3n + 3,
g(3n + 3) = 3n + 1, for all n ≥ 0.
Then which of the following statements is true?
(a) There exists an onto function f : N → N such that fog = f
(b) There exists a one-one function f : N → N such that fog = f
(c) gogog = g
(d) There exists a function : f : N → N such that gof = f
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
g : N → N
g(3n + 1) = 3n + 2,
g(3n + 2) = 3n + 3,
g(3n + 3) = 3n + 1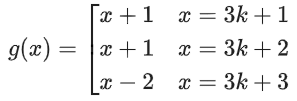
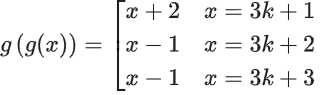
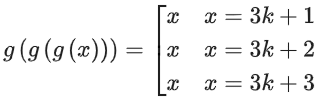
If f : N → N, if is a one-one function such that f(g(x)) = f(x) ⇒ g(x) = x, which is not the case
If f : N → N f is an onto function
such that f(g(x)) = f(x),
one possibility is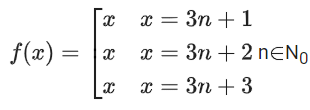
Here f(x) is onto, also f(g(x)) = f(x) ∀ x∈N
Q21. If the domain of the function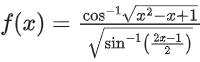 is the interval (α, β], then α + β is equal to:
is the interval (α, β], then α + β is equal to:
(a) 3/2
(b) 2
(c) 1/2
(d) 1
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
O ≤ x2 − x + 1 ≤ 1
⇒ x2 − x ≤ 0
⇒ x ∈ [0, 1]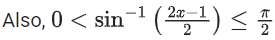
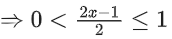
⇒ 0 < 2x − 1 ≤ 2
1 < 2x ≤ 3
1/2 < x ≤ 3/2
Taking intersection
x ∈ (1/2, 1]
⇒ α = 1/2, β = 1
⇒ α + β = 3/2
Q22. The number of solutions of sin7x + cos7x = 1, x∈ [0, 4π] is equal to
(a) 11
(b) 7
(c) 5
(d) 9
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
sin7x ≤ sin2x ≤ 1 ...... (1)
and cos7x ≤ cos2x ≤ 1 ..... (2)
also sin2x + cos2x = 1
⇒ equality must hold for (1) & (2)
⇒ sin7x = sin2x & cos7x = cos2x
⇒ sin x = 0 & cos x = 1
or
cos x = 0 & sin x = 1
⇒ x = 0, 2π, 4π, π/2, 5π/2
⇒ 5 solutions
Q23. Let [x] denote the greatest integer less than or equal to x. Then, the values of x∈R satisfying the equation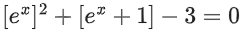 lie in the interval:
lie in the interval:
(a) [0, 1/e)
(b) [loge2, loge3)
(c) [1, e)
(d) [0, loge2)
 View Answer
View Answer 
Correct Answer is Option (d)
Solution: 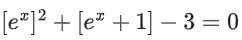
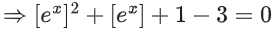
Let [ex] = t
⇒ t2 + t − 2 = 0
⇒ t = −2, 1
[ex] = −2 (Not possible)
or [ex] = 1 ∴ 1 ≤ ex < 2
⇒ ln(1) ≤ x < ln(2)
⇒ 0 ≤ x < ln(2)
⇒ x ∈ [0, In 2)
Q24. Let f : R − {α/6} → R be defined by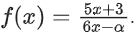 Then the value of α for which (fof)(x) = x, for all x ∈ R − {α/6}, is:
Then the value of α for which (fof)(x) = x, for all x ∈ R − {α/6}, is:
(a) No such α exists
(b) 5
(c) 8
(d) 6
 View Answer
View Answer 
Correct Answer is Option (b)
Solution: 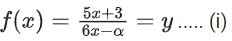
5x + 3 = 6xy − αy
x(6y − 5) = αy + 3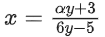
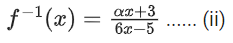
fo f(x) = x
f(x) = f−1(x)
From eqn (i) & (ii)
Clearly (α = 5)
Q25. Let [ x ] denote the greatest integer ≤ x, where x ∈ R. If the domain of the real valued function f(x)=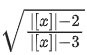 is (− ∞, a) ]∪ [b, c) ∪ [4, ∞), a < b < c, then the value of a + b + c is:
is (− ∞, a) ]∪ [b, c) ∪ [4, ∞), a < b < c, then the value of a + b + c is:
(a) 8
(b) 1
(c) -2
(d) -3
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
For domain, 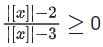
Case I:
When |[x]|−2 ≥ 0
and |[x]|−3 > 0
∴ x ∈ (− ∞, −3) ∪ [4, ∞) ...... (1)
Case II:
When |[x]|−2 ≤ 0
and |[x]|−3 < 0
∴ x ∈ [−2, 3) ..... (2)
So, from (1) and (2) we get
Domain of function
= (− ∞, −3) ∪ [−2, 3) ∪ [4, ∞)
∴ (a + b + c) = −3 + (−2) + 3 = −2 (a < b < c)
⇒ Option (c) is correct.
Q26. Let f : R − {3} → R − {1} be defined by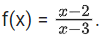
Let g : R → R be given as g(x) = 2x − 3. Then, the sum of all the values of x for which f−1(x) + g−1(x) = 13/2 is equal to:
(a) 3
(b) 5
(c) 2
(d) 7
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
Finding inverse of f(x)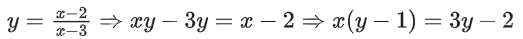
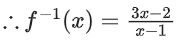
Similarly for g−1(x)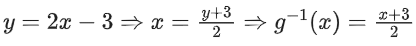
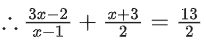
⇒ 6x − 4 + x2 + 2x − 3 = 13x − 13
⇒ x2 − 5x + 6 = 0
⇒ (x − 2)(x − 3) = 0
⇒ x = 2 or 3
Q27. If the functions are defined as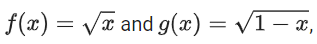 then what is the common domain of the following functions:
then what is the common domain of the following functions: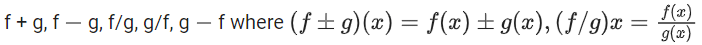
(a) 0 ≤ x ≤ 1
(b) 0 ≤ x < 1
(c) 0<x<1
(d) 0 < x ≤ 1
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: 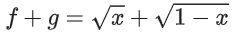
⇒ x ≥ 0 & 1 − x ≥ 0 ⇒ x ∈ [0, 1]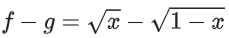
⇒ x ≥ 0 & 1 − x ≥ 0 ⇒ x ∈[0, 1]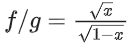
⇒ x ≥ 0 & 1 − x > 0 ⇒ x ∈ [0, 1)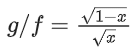
⇒ 1 − x ≥ 0 & x > 0 ⇒ x ∈ (0, 1]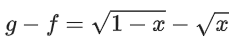
⇒ 1 − x ≥ 0 & x ≥ 0 ⇒ x ∈ [0, 1]
⇒ x ∈ (0, 1)
Q28. The real valued function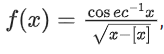 where [x] denotes the greatest integer less than or equal to x, is defined for all x belonging to:
where [x] denotes the greatest integer less than or equal to x, is defined for all x belonging to:
(a) all real except integers
(b) all non-integers except the interval [ −1, 1 ]
(c) all integers except 0, −1, 1
(d) all real except the interval [ −1, 1 ]
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
Domain of cosec−1x:
x ∈ (−∞, −1] ∪ [1, ∞)
and, x − [x] > 0
⇒ {x} > 0
⇒ x ≠ I
∴ Required domain = (−∞, −1] ∪ [1, ∞)− I
Q29. Consider the function f : R → R defined by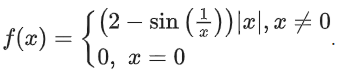 Then f is:
Then f is:
(a) not monotonic on (−∞, 0) and (0, ∞)
(b) monotonic on (0, ∞) only
(c) monotonic on (−∞, 0) only
(d) monotonic on (−∞, 0) ∪ (0, ∞)
 View Answer
View Answer 
Correct Answer is Option (a)
Solution: 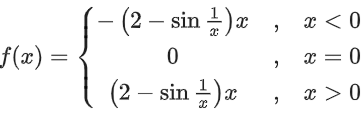
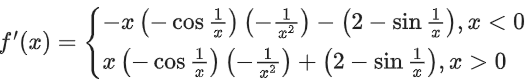
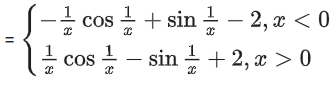
∴ f'(x) is an oscillating function which is non-monotonic on (−∞, 0) and (0, ∞).
Q30. In a school, there are three types of games to be played. Some of the students play two types of games, but none play all the three games. Which Venn diagrams can justify the above statement? 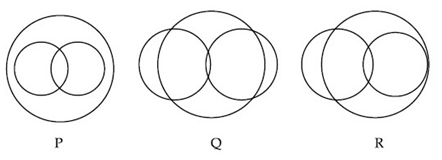 (a) Q and R
(a) Q and R
(b) None of these
(c) P and R
(d) P and Q
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
As none play all three games the intersection of all three circles must be zero.
Hence none of P, Q, R justify the given statement.
Q31. The inverse of y = 5logx is:
(a) x = 5logy
(b)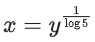
(c)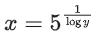
(d) x = ylogy5
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
y = 5logx
⇒ logy = logx . log5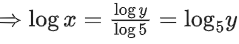
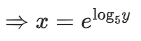
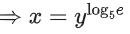
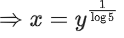
Q33. Let A = {2, 3, 4, 5, ....., 30} and '≃' be an equivalence relation on A × A, defined by (a, b) ≃ (c, d), if and only if ad = bc. Then the number of ordered pairs which satisfy this equivalence relation with ordered pair (4, 3) is equal to:
(a) 5
(b) 6
(c) 8
(d) 7
 View Answer
View Answer 
Correct Answer is Option (d)
Solution:
ad = bc
(a, b) R (4, 3) ⇒ 3a = 4b
b must be multiple of 3
b = {3, 6, 9 ..... 30}
(a, b) = {(4, 3), (8, 16), (12, 9), (16, 12), (20, 15), (24, 18), (28, 21)}
⇒ 7 ordered pair
Q34. Let f be a real valued function, defined on R − {−1, 1} and given by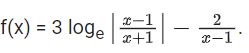
Then in which of the following intervals, function f(x) is increasing?
(a) (−∞, −1) ∪ ([1/2, ∞) − {1})
(b) (−∞, ∞) − {−1, 1)
(c) (−∞, 1/2] − {−1}
(d) (−1, 1/2]
 View Answer
View Answer 
Correct Answer is Option (a)
Solution: 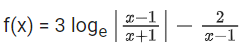
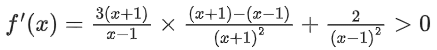
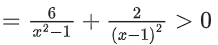
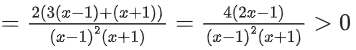
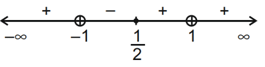
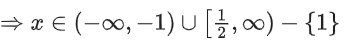
Q35. The range of a ∈ R for which the function f(x) = (4a − 3)(x + loge 5) + 2(a − 7) cot(x/2) sin2(x/2), x ≠ 2nπ, n∈N has critical points, is:
(a) [1, ∞)
(b) (−3, 1)
(c)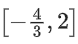
(d) (−∞, −1]
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: 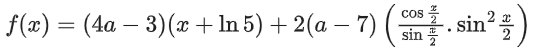
f(x) = (4a − 3)(x + ln 5) + (a − 7)sin x
f′(x) = (4a − 3) + (a − 7)cos x = 0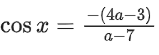
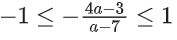
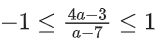
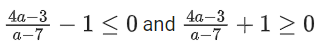
Q36. Let [ x ] denote greatest integer less than or equal to x. If for n ∈ N,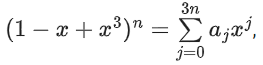
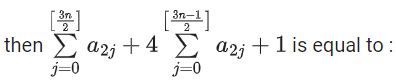
(a) 2n-1
(b) n
(c) 2
(d) 1
 View Answer
View Answer 
Correct Answer is Option (d)
Solution: 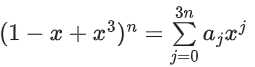
(1 − x + x3) = a0 + a1x + a2x2 + ...... + a3n x 3n
Put x = 1
1 = a0 + a1 + a2 + a3 + a4 + ........ + a3n ...... (1)
Put x = −1
1 = a0 − a1 + a2 − a3 + a4 + ........(−1)3na3n ..... (2)
Add (1) + (2)
⇒ a0 + a2 + a4 + a6 + ...... = 1
Sub (1) − (2)
⇒ a1 + a3 + a5 + a7 + ...... = 0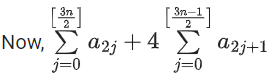
= (a0 + a2 + a4 + ......) + 4(a1 + a3 + .....)
= 1 + 4 × 0
= 1
Q37. The number of elements in the set {x ∈ R : (|x| − 3) |x + 4| = 6} is equal to:
(a) 4
(b) 2
(c) 3
(d) 1
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
Case 1:
x ≤ −4
(−x − 3)(−x − 4) = 6
⇒ (x + 3)(x + 4) = 6
⇒ x2 + 7x + 6 = 0
⇒ x = −1 or −6
but x ≤ −4
x = −6
Case 2:
x ∈ (−4, 0)
(−x − 3)(x + 4) = 6
⇒ −x2 − 7x − 12 − 6 = 0
⇒ x2 + 7x + 18 = 0
D < 0 No solution
Case 3:
x ≥ 0
(x − 3)(x + 4) = 6
⇒ x2 + x − 12 − 6 = 0
⇒ x2 + x − 18 = 0
Q38. Let A = {1, 2, 3, ...., 10} and f : A → A be defined as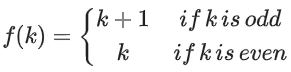
Then the number of possible functions g : A → A such that gof = f is:
(a) 55
(b) 105
(c) 5!
(d) 10C5
 View Answer
View Answer 
Correct Answer is Option (b)
Solution: 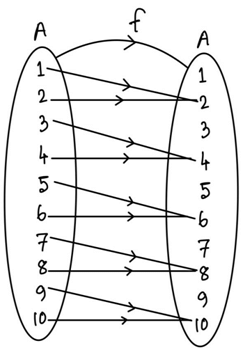
f(1) = 2
f(2) = 2
f(3) = 4
f(4) = 4
f(5) = 6
f(6) = 6
f(7) = 8
f(8) = 8
f(9) = 10
f(10) = 10
∴ f(1) = f(2) = 2
f(3) = f(4) = 4
f(5) = f(6) = 6
f(7) = f(8) = 8
f(9) = f(10) = 10
Given, g(f(x)) = f(x)
when x = 1, g(f(1)) = f(1) ⇒ g(2) = 2
when, x = 2, g(f(2)) = f(2) ⇒ g(2) = 2
∴ x = 1, 2, g(2) = 2
Similarly, at x = 3, 4, g(4) = 4
at x = 5, 6, g(6) = 6
at x = 7, 8, g(8) = 8
at x = 9, 10, g(10) = 10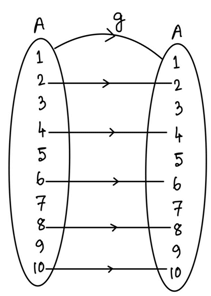
Here, you can see for even terms mapping is fixed. But far odd terms 1, 3, 5, 7, 9 we can map to any one of the 10 elements.
∴ For 1, number of functions = 10
For 3, number of functions = 10
For 9, number of functions = 10
∴ Total number of functions = 10 × 10 × 10 × 10 × 10 = 105
Q39. Let R = {(P, Q) | P and Q are at the same distance from the origin} be a relation, then the equivalence class of (1, −1) is the set:
(a) S = {(x, y)|x2 + y2 = √2}
(b) S = {(x, y)|x2 + y2 = 2}
(c) S = {(x, y)|x2 + y2 = 1}
(d) S = {(x, y)|x2 + y2 = 4}
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
Given R = {(P, Q) | P and Q are at the same distance from the origin}.
Then equivalence class of (1, −1) will contain al such points which lies on circumference of the circle of centre at origin and passing through point (1, −1).
i.e., radius of circle = 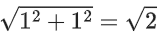
∴ Required equivalence class of (S)
{(x, y)|x2 + y2 = 2}
Q40. Let x denote the total number of one-one functions from a set A with 3 elements to a set B with 5 elements and y denote the total number of one-one functions form the set A to the set A × B. Then:
(a) 2y = 273x
(b) y = 91x
(c) 2y = 91x
(d) y = 273x
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
Number of elements in A = 3
Number of elements in B = 5
Number of elements in A × B = 15
Number of one-one function
x = 5 × 4 × 3
x = 60
Number of one-one function
y = 15 × 14 × 13
y = 15 × 4 × 14/4 × 13
y = 60 × 7/2 × 13
2y = (13)(7x)
2y = 91x
Q41. A function f(x) is given by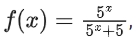 then the sum of the series
then the sum of the series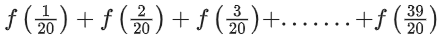 is equal to:
is equal to:
(a) 39/2
(b) 19/2
(c) 49/2
(d) 29/2
 View Answer
View Answer 
Correct Answer is Option (a)
Solution: 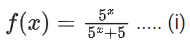
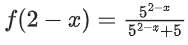
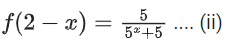
Adding equation (i) and (ii)
f(x) + f(2 − x) = 1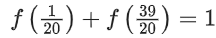
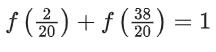
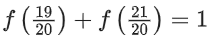
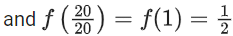
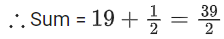
Q42. Let f, g : N → N such that f(n + 1) = f(n) + f(1) ∀ n ∈ N and g be any arbitrary function. Which of the following statements is NOT true?
(a) If g is onto, then fog is one-one
(b) f is one-one
(c) If f is onto, then f(n) = n ∀ n ∈ N
(d) If fog is one-one, then g is one-one
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
f(n + 1) = f(n) + 1
f(2) = 2f(1)
f(3) = 3f(1)
f(4) = 4f(1)
f(n) = nf(1)
f(x) is one-one
Q43. Let f : R → R be defined as f (x) = 2x – 1 and g : R - {1} → R be defined as g(x) =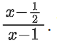 Then the composition function f(g(x)) is:
Then the composition function f(g(x)) is:
(a) one-one but not onto
(b) onto but not one-one
(c) both one-one and onto
(d) neither one-one nor onto
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
Given, f(x) = 2x − 1; f : R → R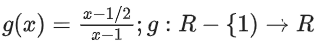
f[g(x)] = 2g(x) − 1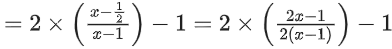
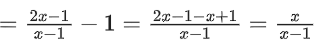
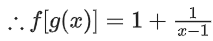
Now, draw the graph of 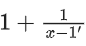
∵ Any horizontal line does not cut the graph at more than one points, so it is one-one and here, co-domain and range are not equal, so it is into.
Hence, the required function is one-one into.
2020
Q1. If g(x) = x2 + x - 1 and (gof) (x) = 4x2 - 10x + 5, then f (5/4) is equal to
(a) 3/2
(b) - 1/2
(c) 1/2
(d) - 3/2
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
We have
g(x) = x2 + x - 1 and (gof) (x) = 4x2 - 10x + 5
Now, g(f(x)) = 4x2 - 10x + 5 = 4x2 - 8x + 4 - 2x +1
⇒ g(f(x)) = (4 - 8x + 4x2) + (2 - 2x) - 1
⇒ g(f(x)) = (2-2x)2 + (2-2x) - 1 ⇒ f(x) = 2 - 2x
Hence,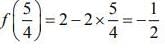
Q2. The inverse function of f(x)
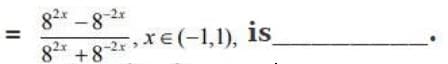
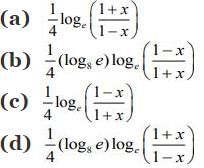
 View Answer
View Answer 
Correct Answer is Option (d)
Solution:
Let,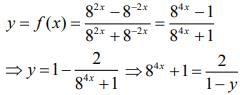
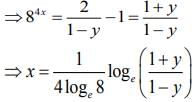
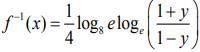
Q3. Let f: (1, 3) → R be a function defined by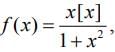
where [x] denotes the greatest integer ≤ x . Then, the range of f is 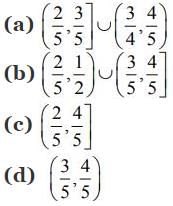
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
We have,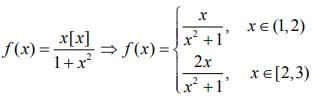
Since f(x) is a decreasing function, then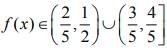
Q4. Let f and g be differentiable functions on R such that fog is the identity function. If for some a, b ∈ R g'(a) = 5 and g(a) = b then f'(b) is equal to
(a) 1/5
(b) 1
(c) 5
(d) 2/5
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
f and g are differentiable functions on R and fog is the identity function. So,
f(g(x)) = x
⇒ f'(g(x)) . g'(x) = 1 (1)
Substituting x = a in EQ (1), we get
f'(g(a)). g'(a) = 1
⇒ f'(b) × 5 = 1 ⇒ f'(b) = 1/5
2019
Q1. For x ∈ R - {0, 1}, let f1(x) = 1/x, f2 (x) = 1 - x and f3(x) = 1/1-x be three given functions. If a function, J(x) satisfies (f2oJof1) (x) = f3(x) then J(x) is equal to:
(a) f3(x)
(b) 1/x f3(x)
(c) f2(x)
(d) f1(x)
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
The given relation is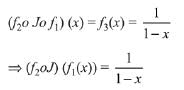
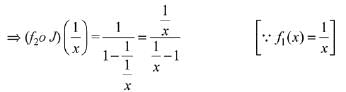

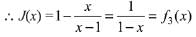
Q2. If the fractional part of the number 2403/15 is k/15, then k is equal to:
(a) 6
(b) 8
(c) 4
(d) 14
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
2403 = 2400 · 23
= 24 × 100 · 23
= (24)100· 8
= 8(24)100 = 8(16)100
= 8(1 + 15)100
= 8 + 15μ
When 2403 is divided by 15, then remainder is 8.
Hence, fractional part of the number is 8/15
Therefore, value of k is 8
Q3. Let A = {x ∈ R: x is not a positive integer}. Define a function f: A → R as f(x) = 2x/x - 1, then f is:
(a) Not injective
(b) Neither injective nor surjective
(c) Surjective but not injective
(d) Injective but not surjective
 View Answer
View Answer 
Correct Answer is Option (d)
Solution:
As A = {x ∈ R: x is not a positive integer}
A function f: A → R given by f(x) = 2x/x-1
f(x1) = f(x2) ⇔ x1 = x2
So, f is one-one.
As f(x) ≠ 2 for any x ∈ A ⇒ f is not onto.
Hence f is injective but not subjective.
Q4. Let N be the set of natural numbers and two functions f and g be defined as f, g : N → N such that 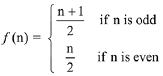
and g(n) = n - (- 1)n. Then fog is:
(a) Onto but not one-one.
(b) One-one but not onto.
(c) Both one-one and onto.
(d) Neither one-one nor onto.
 View Answer
View Answer 
Correct Answer is Option (a)
Solution: 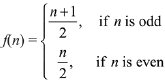
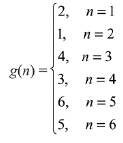
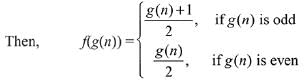
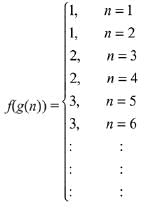
⇒ fog is onto but not one - one
Q5. Let f: R → R be defined by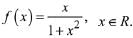
Then the range of f is:
(a) [- 1/2, 1/2]
(b) R - [-1,1]
(c) R - [- 1/2, 1/2]
(d) (-1,1) - {0}
 View Answer
View Answer 
Correct Answer is Option (a)
Solution: 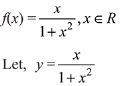
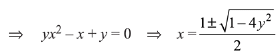
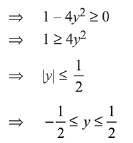
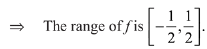
Q6. Let a function f: (0, ∞) → (0, ∞) be defined by
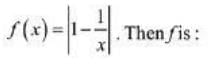 (a) Not injective but it is surjective
(a) Not injective but it is surjective
(b) Injective only
(c) Neither injective nor surjective
(d) Both injective as well as surjective
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
f: (0, ∞) → (0, ∞)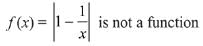
∵ f(1) = 0 and 1 ∈ domain but 0 ∉ co-domain
Hence, f(x) is not a function.
Q7. If f(x) = loge(1 - x)/(1 + x) , |x| < 1, then f(2x/1 + x2) is equal to :
(a) 2f(x)
(b) 2f(x2)
(c) (f(x))2
(d) -2f(x)
 View Answer
View Answer 
Correct Answer is Option (a)
Solution: 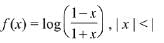
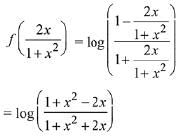
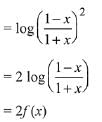
Q8. Let f(x) = ax (a > 0) be written as f(x) = f1(x) + f2(x), where f1(x) is an even function and f2(x) is an odd function. Then f1(x + y) + f1(x - y) equals:
(a) 2 f1(x) f1(y)
(b) 2 f1(x + y) f1(x - y)
(c) 2 f1(x) f2(y)
(d) 2 f1(x + y) f2(x - y)
 View Answer
View Answer 
Correct Answer is Option (a)
Solution:
Given function can be written as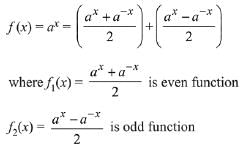
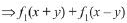
Q9. If the function f: R - {1, -1} → A defined by f(x) = x2/1 - x2, is surjective, then A is equal to:
(a) R - {-1}
(b) [0, ∞]
(c) R- [-1, 0]
(d) R - (-1, 0]
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: 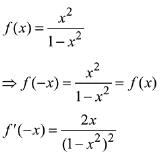
∴ f(x) increases in x ∈ (0, ∞)
Also f(0) = 0 and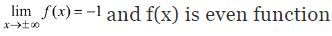
∴ Set A = R - [-1, 0)
And the graph of function f(x) is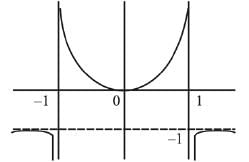
Q10. 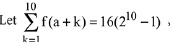
where the function f satisfies f(x + y) = f(x) f(y) for all natural numbers x, y and f(1) = 2. Then the natural number 'a' is:
(a) 2
(b) 16
(c) 4
(d) 3
 View Answer
View Answer 
Correct Answer is Option (d)
Solution:
∵ f(x + y) = f(x) x f(y)
⇒ Let f(x) = tx
∵ f(1) = 2
∵ t = 2
⇒ f(x) = 2x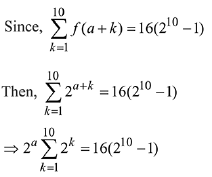
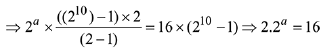
⇒ a = 3
Q11. The domain of the definition of the function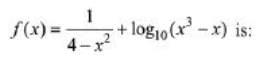 (a) (-1, 0) ∪ (1, 2) ∪ (3, ∞)
(a) (-1, 0) ∪ (1, 2) ∪ (3, ∞)
(b) (-2, -1) ∪ (-1, 0) ∪ (2, ∞)
(c) (-1, 0) ∪ (1, 2) ∪ (2, ∞)
(d) (1, 2) ∪ (2, ∞)
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
To determine domain, denominator ≠ 0 and x3 - x > 0
i.e., 4 - x2 ≠ 0 x ≠ ±2 ...(1)
and x (x - 1) (x + 1) > 0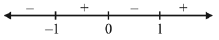
x∈(-1, 0) ∪ (1, ∞) ...(2)
Hence domain is intersection of (1) & (2).
i.e.,x ∈ (-1, 0) ∪ (1, 2) ∪ (2, ∞)
Q12. Let f(x) = x2, x ∈ R. For any A ⊆ R, define g(A) = {x∈R: f(x) ∈ A}. If S = [0, 4], then which one of the following statements is not true?
(a) g(f(S)) ≠ S
(b) f(g(S)) = S
(c) g(f(S)) = g(S)
(d) f (g (S)) ≠ f (S)
 View Answer
View Answer 
Correct Answer is Option (c)
Solution:
f(x) = x2 ; x ∈ R
g(A) = {x ∈ R: f(x) ∈ A} S = [ 0, 4]
g(S) = {x ∈ R: f(x) ∈ S}
= {x ∈ R: 0 ≤ x2 ≤ 4} = { x ∈ R : -2 ≤ x ≤ 2}
∴ g(S) ≠ S
∴ f(g (S)) ≠ f(S)
g(f(S)) = {x ∈ R: f(x) ∈ f(S)}
= { x ∈ R : x2 ∈ S2} = { x ∈ R : 0 ≤ x2 ≤ 16}
= {x ∈ R : -4 ≤ x ≤ 4}
∴ g(f(S)) ≠ g(S)
∴ g(f(S)) = g (S) is incorrect.
Q13. Let f(x) = loge (sinx), (0 < x < π) and g(x) = sin-1 (e-x), (x > 0). If α is a positive real number such that a = (fog)' (α) and b = (fog) (α), then:
(a) aα2 + bα + a = 0
(b) aα2 - bα - a = 1
(c) aα2 - bα - a = 0
(d) aα2 + bα - a = - 2a2
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
f(x) = ln (sin x), g (x) = sin-1 (e-x)
⇒ f(g(x)) = ln (sin (sin-1 e-x)) = - x
⇒ f(g(α)) = - α
But given that (fog) (α) = b
∴ - α = b and f' (g(α)) = a, i.e., a = - 1
∴ aα2 - bα - a = - α2 + a2 - (- 1)
⇒ aα2 - bα - a = 1
Q14. For x ∈ (0, 3/2), let f(x) = √x, g(x) = tan x and h(x) = (1-x2)/1+x2). If φ(x) = ((hof)og), (x), then φ (π/3) is equal to:
(a) tan π/12
(b) tan 11π/12
(c) tan 7π/12
(d) tan 5π/12
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
∵ φ(x) = ((hof)og)(x)
∵ φ(π/3) = h(f(g(π/3))) = h(f(√3)) = h(31/4)
= (1 - √3)/(1+√3) = - 1/2 (1 + 3 - 2√3) = √3 - 2 = -(-√3 + 2)
= -tan 15º = tan(180º - 15º) = tan(π - π/12) = tan 11π/12
2017
Q1. Let f(x) = 210dx + 1 and g(x) = 310x - 1. If (fog)(x) = x, then x is equal to:
(a) (210 - 1)/(210 - 3-10)
(b) (1 - 2-10)/(310 - 2-10)
(c) (310 - 1)/(310 - 2-10)
(d) (1 - 3-10)/(210 - 3-10)
 View Answer
View Answer 
Correct Answer is Option (b)
Solution:
f(g(x)) = x
f(310x - 1) = 210(310.x - 1) = x
= 1/(310 - 2-110)
210(310x - 1) + 1 = x
x(610 - 1) = 210 - 1
x = (210 - 1)/(610 - 1) = (1 - 2-10)/(310 - 2-10)
Q2. The function f: N → N defined by f(x) = x - 5[x/5], where N is the set of natural numbers and [x] denotes the greatest integer less than or equal to x, is:
(a) One-one but not onto
(b) One-one and onto
(c) Neither one-one nor onto
(d) Onto but not one-one
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: 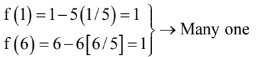
f(10) = 10 – 5(2) = 0 which is not in codomain
So, the function is many one + into
2016
Q1. If f(x) + 2f(1/x) = 3x, x ≠ 0, and S = {x ∈ R: f(x) = f(-x)}; then S:
(a) Is an empty set
(b) Contains exactly one element
(c) Contains exactly two elements.
(d) Contains more than two elements.
 View Answer
View Answer 
Correct Answer is Option (c)
Solution: 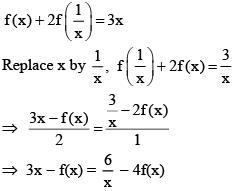
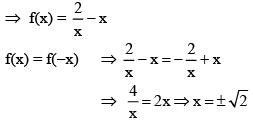
|
203 videos|307 docs|139 tests
|
FAQs on JEE Main Previous Year Questions (2016- 2025): Functions - Mathematics (Maths) Class 12
| 1. What is a function in mathematics? |  |
| 2. How do we represent a function in mathematics? |  |
| 3. What is the difference between a domain and a range of a function? |  |
| 4. How do we find the inverse of a function? |  |
| 5. What is a composite function? |  |