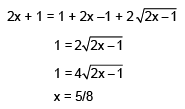JEE Main Previous Year Questions (2016- 2025): Quadratic Equation and Inequations (Inequalities) PDF Download

Q.1. Let α and β be two real roots of the equation (k + 1)tan²x  - √2 λ tan x =  (1-k), where k (≠ - 1) and λ are real numbers. If 2 tan2(α + β) = 50, then a value of λ is    (2020)
(1) 10√2
(2) 10
(3) 5
(4) 5√2
Ans. (2)
Solution. The given quadratic equation is
(k + 1)tan²x - √2λ tan x + (k - 1) = 0
Given that α and β be the two real roots of the given equation, then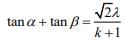
 ...(1)
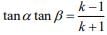 ...(2)
Now,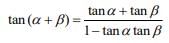


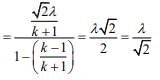
Now, tan²(α + β) = 50 ⇒ λ²/2  = 50
⇒ λ² = 100 ⇒ λ = ±10

Q.2. Let α and β be the roots of the equation x² - x - 1 = 0. If p_k = (α)^k + (β)^k, k ≥ 1, then which one of the following statements is not true?    (2020)
(1) p₃ = p₅ - p₄
(2) p₅ = 11
(3) (p₁ + p₂ + p₃ + p₄ + p₅) = 26
(4) p₅ = p₂.p₃
Ans. (4)
Solution. Given, α and β be the roots of the equation x² - x - 1 = 0. Therefore,
α + β = 1 and αβ = -1
Now, p_k = (α)^k + (β)^k
p₁ = α + β  = 1 ...(1)
p₂ = α² + β² = (α + β)² - 2αβ
⇒ p2 = 1 + 2 = 3 ...(2)
p₃ = α³ + β³ = (α + β)³ - 3αβ(α + β)
p₃ = 1 + 3 = 4 ...(3)
Since α and β be the roots of the equation x² - x − 1 = 0, then
α² - α - 1 = 0 ⇒ α^k - α^k-1 - α^k-2 = 0 ...(4)
β² - β - 1 = 0 ⇒ β^k - β^k-1 - β^k-2 = 0 ...(5)
From Eqs. (4) and 5, we get p_k = p_k-1 + p_k-2. Hence, p₄ = 7 and p₅ = 11 ⇒ p₅ ≠ p₂.p₃

Q.3. If the equation x² + bx + 45 = 0 (b ∈ R) has conjugate complex roots and they satisfy |z+1| = 2√10, then    (2020)
(1) b² - b = 30
(2) b² + b = 72
(3) b² - b = 42
(4) b² + b = 12
Ans. (1)
Solution. Let z = α ± iβ be the roots of the x² + bx + 45 = 0, then
α + iβ + α - iβ = -b ⇒ 2α = -b ...(1)
(α + iβ)(α - iβ) = 45 ⇒ (α² + β²) = 45 ...(2)
The roots satisfy the equation |z + 1| = 2√10, then
(α + 1)² + β² = 40 ...(3)
From Eqs. (2) and (3), we get
(α + 1)² - α² = -5 ⇒ 2α + 1 = -5 ⇒ α = -3
Hence, b² + b = (-6)² - 6 = 30

Q.4. The least positive value of ‘a’ for which the equation 2x² +(a-10)x+ 33/2 = 2a has real roots is _____.    (2020)
Ans. (8.00)
Solution. The equation 2x² +(a-10)x + 33/2 = 2a has real roots, therefore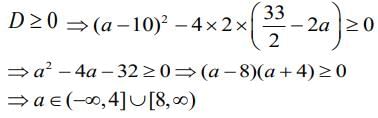

Hence, the least positive value of ‘a’ is 8.

Q.5. Let 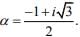 If 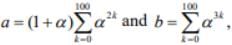 then a and b are the roots of the quadratic equation    (2020)
(1) x² + 101x + 100 = 0
(2) x² - 102x + 101 = 0
(3) x² - 101x + 100 = 0
(4) x2 + 102x + 101 = 0
Ans. (2)
Solution. Given,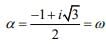

Now,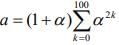


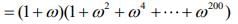
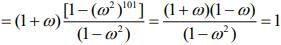 (since ω³ = 1)
b = 1 + ω³ + ω⁶ + ... + ω³⁰⁰ = 101
Hence, the equation of quadratic equation is
x² - (a + b)x + ab = 0 ⇒ x² - 102x  + 101 = 0

Q.6. Let 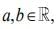 a ≠ 0 be such that the equation ax² - 2bx  + 5 = 0 has a repeated root α, which is also a root of the equation x² - 2bx - 10 = 0. If β  is the other root of this equation, then α² + β² is equal to    (2020)
(1) 25
(2) 26
(3) 28
(4) 24
Ans. (1)
Solution. The equation ax² - 2bx + 5 = 0 has a repeated root α, then
D = 0 ⇒ 4b² - 4 . a . 5 = 0 ⇒ b² = 5a ...(1)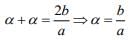
 ...(2)
Since α is also, the root of equation x² - 2bx - 10 = 0. So,
α² - 2bα - 10 = 0 ...(3)
aα² - 2bα + 5 = 0 ...(4)
From Eqs. (3) and (4), we get
(a - 1)α² + 15 = 0 ⇒ (a - 1)b² + 15a² = 0
⇒ (a - 1) x 5a +15a² = 0 ⇒ 20a² - 5a = 0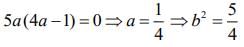

Now, α + β = 2b and αβ = -10
Hence, (α + β)² = α² + β² + 2αβ = 4b²
⇒α² + β² = 5 - 2(-10) = 25

Q.7. Let α and β be two roots of the equation x² + 2x + 2 = 0, then α¹⁵ +β¹⁵ is equal to:   (2019)
(1) -256    
(2) 512
(3) -512    
(4) 256
Ans. (1)
Solution. Consider the equation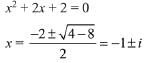




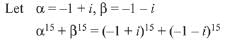
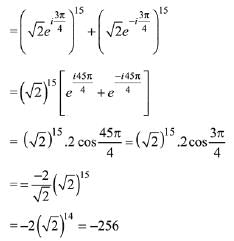
Q.8. If both the roots of the quadratic equation x² - mx + 4 = 0 are real and distinct and they lie in the interval [1,5], then m lies in the interval:    (2019)
(1) (-5,-4)    
(2) (4,5)
(3) (5,6)    
(4) (3,4)
Ans. (2)
Solution. Given quadratic equation is: x² -mx + 4 = 0 Both the roots are real and distinct.
So, discriminant b² - 4ac > 0.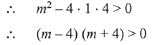

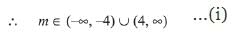
Since, both roots lies in [1, 5]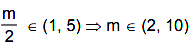
....(ii)
And 1 · (1 - m + 4) > 0 ⇒ m < 5
∴ m ∈(∞ - 5)   ...(iii)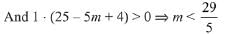

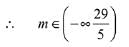   ...(iv)
From (i), (ii), (iii) and (iv), m ∈ (4, 5)

Q.9. The number of all possible positive integral values of α for which the roots of the quadratic equation, 6x² - 11x + α = 0 are rational numbers is:    (2019)
(1) 3    
(2) 2
(3) 4    
(4) 5
Ans. (1)
Solution. The roots of 6x² - 11x + α = 0 are rational numbers.
∴ Discriminant D must be perfect square number.
D = (-11)² - 4 · 6 · α
= 121- 24α    must be a perfect square
Hence, possible values for α are
α = 3, 4, 5.
∴ 3 positive integral values are possible.

Q.10. If 5, 5r, 5r² are the lengths of the sides of a triangle, then r cannot be equal to:    (2019)
(1) 3/4
(2) 5/4
(3) 7/4
(4) 3/2
Ans. (3)
Solution.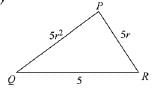

ΔPQR is possible if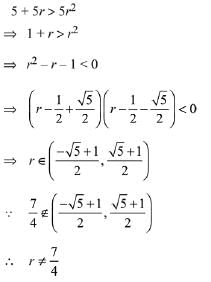


Q.11. Consider the quadratic equation (c - 5)x² - 2cx + (c - 4) = 0, c ≠ 5. Let S be the set of all integral values of c for which one root of the equation lies in the interval (0, 2) and its other root lies in the interval (2, 3). Then the number of elements in S is:    (2019)
(1) 18    
(2) 12    
(3) 10    
(4) 11
Ans. (4)
Solution. Consider the quadratic equation
(c - 5) x² - 2cx + (c - 4) = 0
Now,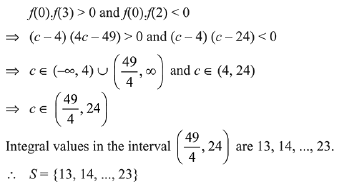


Q.12. The value of λ such that sum of the squares of the roots of the quadratic equation, x² + (3 - λ)x + 2 = λ has the least value is:    (2019)
(1) 15/8   
(2) 1
(3) 4/9   
(4) 2
Ans. (4)
Solution. The given quadratic equation is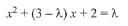

Sum of roots =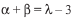
Product of roots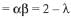

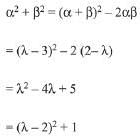
For α²+β² to be minimum, λ=2.

Q.13. If one real root of the quadratic equation 81x² + kx + 256 = 0 is cube of the other root, then a value of k is :    (2019)
(1) -81    
(2) 100
(3) 144    
(4) -300
Ans. (4)
Solution. Let α and β be the roots of the equation.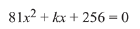




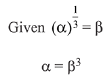
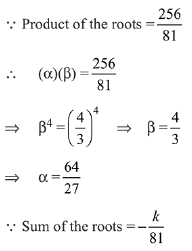
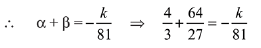
⇒ k = -300

Q.14. If α,β be the ratio of the roots of the quadratic equation in x, 3m²x² + m(m - 4)x + 2 = 0, then the least value of m for which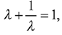 is:    (2019)
(1) 2-√3    
(2) 4-3√2
(3) -2 + √2    
(4) 4-2√3
Ans. (2)
Solution. Let roots of the quadratic equation are α, β.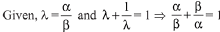


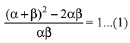
The quadratic equation is, 3m²x² + m(m - 4) x + 2 = 0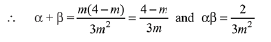

Put these values in eq (1),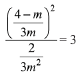


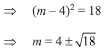
Therefore, least value is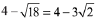

Q.15. The number of integral values of m for which the quadratic expression, (1 + 2m)x² -2(1 + 3m)x + 4(1 + m), x ∈ R, is always positive, is:    (2019)
(1) 3   
(2) 8
(3) 7   
(4) 6
Ans. (3)
Solution. Let the given quadratic expression
(1 + 2m)x² - 2(1 + 3m)x + 4(1 + m), is positive for all x ∈ R, then
1 + 2m > 0   ...(1)
D<0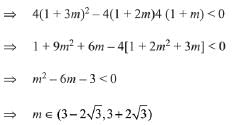

From (1)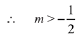


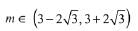
Then, integral values of m = {0, 1,2, 3,4, 5, 6}
Hence, number of integral values of m = 7

Q.16. If α and β be the roots of the equation x² - 2x + 2 = 0, then the least value of n for which 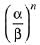= 1 is:    (2019)
(1) 2    
(2) 5    
(3) 4    
(4) 3
Ans. (3)
Solution. The given quadratic equation is x² - 2x + 2 = 0
Then, the roots of the this equation are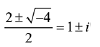

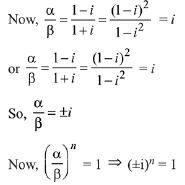
⇒ n must be a multiple of 4.
Hence, the required least value of n = 4.

Q.17. The sum of the solutions of the equation 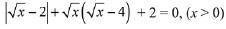 is equal to:    (2019)
(1) 9    
(2) 12    
(3) 4    
(4) 10
Ans. (4)
Solution.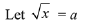

∴ given equation will become: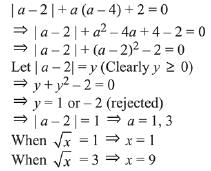

Hence, the required sum of solutions of the equation = 10

Q.18. The number of integral values of m for which the equation (1 + m²)x² - 2(1 + 3m)x + (1 + 8m) = 0 has no real root is:    (2019)
(1) 1    
(2) 2
(3) infinitely many    
(4) 3
Ans. (3)
Solution. Given equation is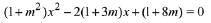

∵ equation has no real solution
D< 0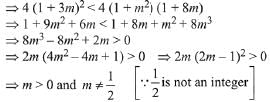

⇒ number of integral values of m are infinitely many.

Q.19. Let p, q ∈ R. If 2 - √3 is a root of the quadratic equation, x² + px + q = 0, then:    (2019)
(1) p²-4q + 12 = 0    
(2) q² - 4p - 16 = 0
(3) q² + 4p + 14 = 0    
(4) p² - 4q - 12 = 0
Ans. (4)
Solution. Since 2 - √3 is a root of the quadratic equation x² + px + q = 0
∴ 2 + √3 is the other root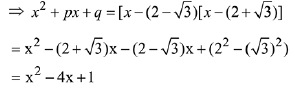

Now, by comparing p = -4, q = 1
⇒ p² - 4q - 12= 16 - 4 - 12 = 0

Q.20. If m is chosen in the quadratic equation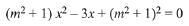

such that the sum of its roots is greatest, then the absolute difference of the cubes of its roots is:    (2019)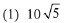




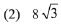
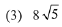
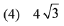
Ans. (3)
Solution.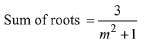

∵ sum of roots is greatest ∴ m = 0
Hence equation becomes x² - 3x + 1 = 0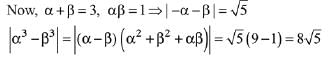


Q.21. If α and β are the roots of the quadratic equation, x² + x sinθ - 2sinθ = 0 0,θ ∈ (0, π/2), then 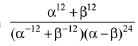 is equal to:    (2019)
(1)
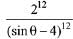
(2)
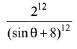
(3)
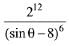
(4)
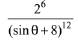
Ans. (2)
Solution. Given equation is, x² + x sinθ - 2 sinθ = 0
α + β = - sinθ and αβ = - 2 sinθ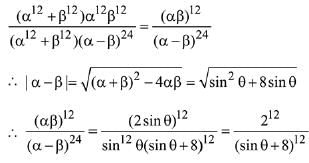


Q.22. The number of real roots of the equation 5 + |2^x -1| = 2^x (2^x - 2) is:    (2019)
(1) 3    
(2) 2    
(3) 4    
(4) 1
Ans. (4)
Solution.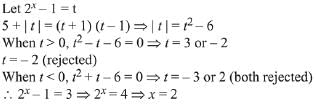


Q.23. Let S = {x ∈ R : x ≥ 0 and 2 |√x - 3| + √x (√x - 6) + 6 = 0}. Then S:   (2018)
(1) is an empty set
(2) contains exactly one element
(3) contains exactly two element
(4) contains exactly four elements
Ans. (3)
Solution.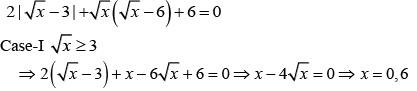


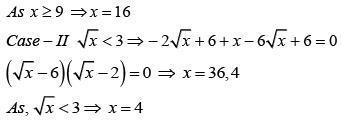
There are exactly two elements in the given set.

Q.24. If λ ϵ R is such that the sum of the cubes of the roots of the equation, x² + (2 - λ)x + (10 - λ) = 0 is minimum, then the magnitude of the difference of the roots of this equation is:    (2018)
(1) 2√5
(2) 20
(3) 2√7
(4) 4√7
Ans. (1)
Solution.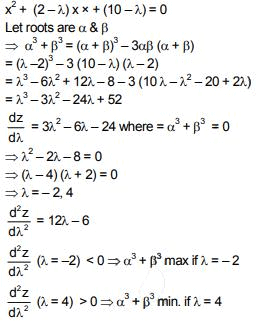 
 


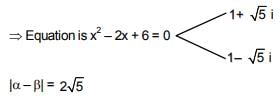
Q.25. Let p, q and r be real numbers (p ≠ q, r ≠ 0), such that the roots of the equation 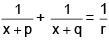 are equal in magnitude but opposite in sign, then the sum of squares of these roots is equal to:    (2018)
(1) p² + q² 
(2)
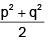
(3) 2(p² + q²)
(4) p² + q² + r² 
Ans. (1)
Solution. (2x + p + q) r = (x + p) (x + q)
x² + (p + q - 2r) x + pq - pr - qr = 0
p + q = 2r    …….. (i)
α² + β² = (α + β)² - 2αβ
= 0 - 2 [pq - pr - qr]  = - 2pq + 2r (p + q)  = - 2pq + (p + q)² = p² + q² 

Q.26. The number of values of k for which the system of linear equations,
(k + 2)x + 10y = k
kx + (k + 3) y = k - 1 has no solution, is:    (2018)
(1) 1
(2) 2
(3) 3
(4) 4
Ans. (1)
Solution. For no solution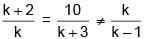
(k + 2) (k + 3) = 10 k
k² - 5k + 6 = 0
⇒ k = 2,3
k ≠ 2  for k = 2 both lines identical
so k = 3 only  
so number of values of k is 1

Q.27. If, for a positive integer n, the quadratic equation, x(x + 1) + (x + 1) (x + 2) + ..... + (x + n - 1) (x + n) = 10n has two consecutive integral solutions, then n is equal to    (2017)
(1) 11
(2) 12
(3) 9
(4) 10
Ans. (1)
Solution.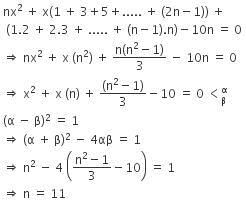 


Q.28. Let p(x) be a quadratic polynomial such that p(0) = 1. If p(x) leaves remainder 4 when divided by x – 1 and it leaves remainder 6 when divided by x + 1, then:    (2017)
(1) p(–2) = 19
(2) p(2) = 19
(3) p(–2) = 11
(4) p(2) = 11
Ans. (1)
Solution. p(x) = ax² + bx + c
p(0) = 1 = c = 1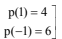


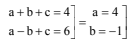
p(x) = 4x² – x + 1
p(–2) = 16 + 2 + 1 = 19

Q.29. The sum of all the real values of x satisfying the equation 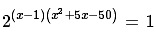 is:    (2017)
(1) 16
(2) –5
(3) –4
(4) 14
Ans. (3)
Solution. (x – 1) (x² + 5x – 50) = 0
⇒ (x – 1) (x + 10) (x – 5) = 0
⇒ x = 1, 5, –10
Therefore, sum = –4

Q.30. The sum of all real values of x satisfying the equation 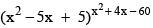 is:    (2016)
(1) 3
(2) -4
(3) 6
(4) 5
Ans. (1)
Solution.


Q.31. If the equations x² + bx – 1 = 0 and x² + x + b = 0 have a common root different from –1, then |b| is equal to    (2016)
(1) √2
(2) 2
(3) √3
(4) 3
Ans. (3)
Solution. x² + bx – 1 = 0 & x² + x + b = 0 have common root α.


Q.32. If x is a solution of the equation, 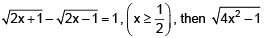 is equal to    (2017)
(1) 2
(2) 3/4
(3) 2√2
(4) 1/2
Ans. (2)
Solution.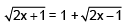

Squaring on both sides