Q.1. The greatest positive integer k, for which 49k + 1 is a factor of the sum 49125 + 49124 + ...+ 492 + 49 + 1, is (2020)
(1) 32
(2) 63
(3) 60
(4) 65
Ans. (2)
Solution. We have
1 + 49 + 492 + .... + 49125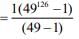
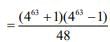
Hence, the greatest positive integer value of k is 63.
Q.2. If the sum of the coefficients of all even powers of x in the product (1 + x + x2 + ... + x2n)(1 - x + x2 - x3 + ... + x2n) is 61, then n is equal to ____.
Ans. 30
Solution. We have
(1 + x + x2 + ... + x2n)(1 - x + x2 - x3 + ... + x2n) = a0 + a1x + a2x2 + a3x3 + ... + a4nx4n
Substituting x = 1, we get
a0 + a1 + a2 + ... + a4n = 2n + 1 (1)
Substituting x = -1 here, we get
a0 - a1 + a2 - a3 + ... + a4n = 2n + 1 (2)
From Eqs. (1) and (2), we get
a0 + a2 + a4 + ... + a4n = 2n + 1 ...(3)
Now, 2n + 1 = 61 ⇒ n = 30
Q.3. The coefficient of x7 in the expression (1 + x)10 + x(1 +x)9 + x2(1 +x)8 + ... + x10 is (2020)
(1) 210
(2) 330
(3) 120
(4) 420
Ans. (2)
Solution. We have
= (1 + x)10 + x(1 +x)9 + x2(1 +x)8 + ... + x10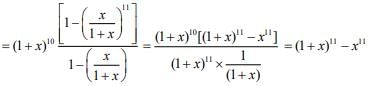
Therefore, the coefficient of x7 in the expression is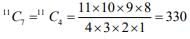
Q.4. If α and β be the coefficients of x4 and x2 respectively in the expansion of  then (2020)
then (2020)
(1) α + β = 60
(2) α + β = -30
(3) α - β = 60
(4) α - β = -132
Ans. (4)
Solution. We have
(x + a)n + (x - a)n = 2(T1 + T3 + T5 + ...) = 2[6C0x6 + 6C2x4(x2 - 1) + 6C4x2(x2 - 1)2 + 6C6(x2 - 1)3]
= 2[6C0x6 + 6C2x4(x2 - 1) + 6C4x2(x2 - 1)2 + 6C6(x2 - 1)3]
= 64x6 - 96x4 + 36x2
Hence, α - β = - 96 - 36 = -132
Q.5. The coefficient of x4 in the expansion of (1 + x + x2)10 is ____. (2020)
Ans. 615
Solution. The general term of the expansion of (1 + x + x2)10 is
For coefficient of x4, β + 2γ = 4. So,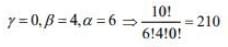 ...(1)
...(1)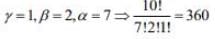 ...(2)
...(2)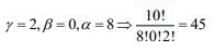 ...(3)
...(3)
Hence, the coefficient of x4 in the expansion of (1 + x + x2)10 is 210 + 360 + 45 = 615.
Q.6. In the expansion of 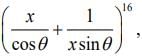 if l1 is the least value of the term independent of x when
if l1 is the least value of the term independent of x when 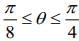 and l2 is the least value of the term independent of x when
and l2 is the least value of the term independent of x when  then the ratio l2 : l1 is equal to (2020)
then the ratio l2 : l1 is equal to (2020)
(1) 1 : 8
(2) 1 : 16
(3) 8 : 1
(4) 16 : 1
Ans. (4)
Solution. The term independent from x in expression 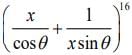 is
is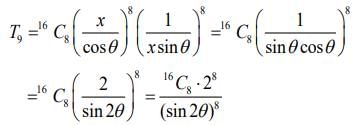
If 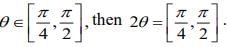 So, l1 = 16C8 . 28 ...(1)
So, l1 = 16C8 . 28 ...(1)
If 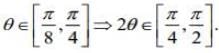 So,
So, 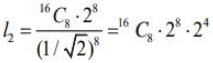 ...(2)
...(2)
Hence, 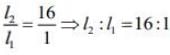
Q.7. The coefficient of t4 in the expansion of 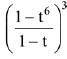 (2019)
(2019)
(1) 14
(2) 15
(3) 10
(4) 12
Ans. (2)
Solution. Consider the expression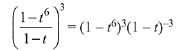

Hence, the coefficient of 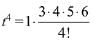
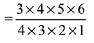
= 15
Q.8. If 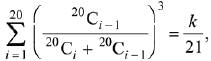 then k equals: (2019)
then k equals: (2019)
(1) 400
(2) 50
(3) 200
(4) 100
Ans. (4)
Solution. Consider the expression, 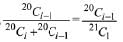
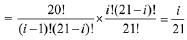
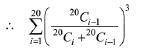
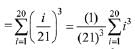
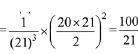
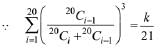
∴ k=100
Q.9. If the third term in the binomial expansion of 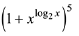 equals 2560, then a possible value of x is: (2019)
equals 2560, then a possible value of x is: (2019)
(1) 1/4
(2) 4√2
(3) 1/8
(4) 2√2
Ans. (1)
Solution. Third term of 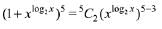
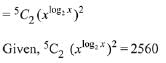
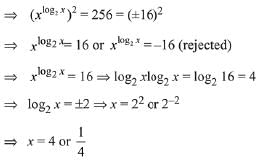
Q.10. The positive value of λ for which the co-efficient of x2 in the expression 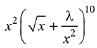 is 720, is: (2019)
is 720, is: (2019)
(1) 4
(2) 2√2
(3) √5
(4) 3
Ans. (1)
Solution. Since, coefficient of x2 in the expression 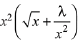 is a constant term, then Coefficient of x2 in x2
is a constant term, then Coefficient of x2 in x2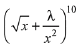 = co-efficient of constant term in
= co-efficient of constant term in 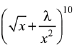
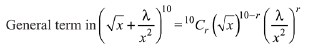

Then, for constant term,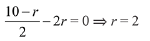
Coefficient of x2 in expression = 10C2λ2 = 720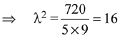
⇒λ = 4
Hence, required value of λ is 4.
Q.11. If 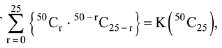 then K is equal to: (2019)
then K is equal to: (2019)
(1) (25)2
(2) 225 - 1
(3) 224
(4) 225
Ans. (4)
Solution.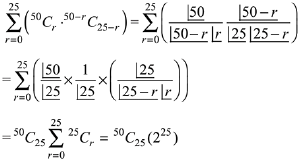
Then, by comparison, K = 225
Q.12. The value of r for which 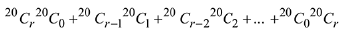 is maximum, is: (2019)
is maximum, is: (2019)
(1) 15
(2) 20
(3) 11
(4) 10
Ans. (2)
Solution. Consider the expression 
For maximum value of above expression r should be equal to 20.
Which is the maximum value of the expression,
So, r = 20.
Q.13. The sum of the real values of x for which the middle term in the binomial expansion of equals 5670 is: (2019)
equals 5670 is: (2019)
(1) 0
(2) 6
(3) 4
(4) 8
Ans. (1)
Solution. Middle Term,  term in the binomial expansion of
term in the binomial expansion of
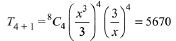
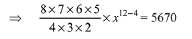
⇒ x8 - 81 = 0
∴ sum of all values of x = sum of roots of equation (x8 - 81 = 0)
Q.14. Let Sn = 1 + q + q2 +.... + qn and 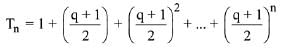
where q is a real number and q ≠ 1. If
101C1 + 101C2·S1 + .... + 101C100·S100 = αT100, then α is equal to: (2019)
(1) 299
(2) 202
(3) 200
(4) 2100
Ans. (4)
Solution.
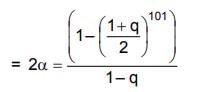
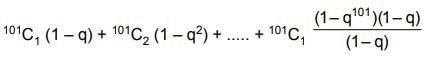
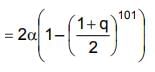
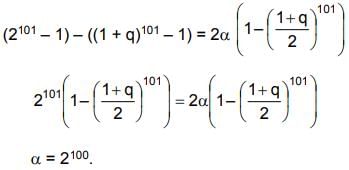
Q.15. Let(x+10)50 + (x-10)50 = ao + a1x+a2x2 + .... + a50x50, for all x ∈ R; then 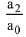 is equal to: (2019)
is equal to: (2019)
(1) 12.50
(2) 12.00
(3) 12.25
(4) 12.75
Ans. (3)
Solution. 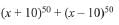

= 12.25
Q.16. A ratio of the 5th term from the beginning to the 5th term from the end in the binomial expansion of 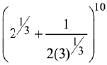 is: (2019)
is: (2019)
(1) 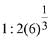
(2) 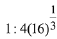
(3) 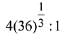
(4) 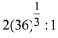
Ans. (3)
Solution.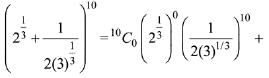
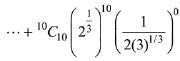
5th term from beginning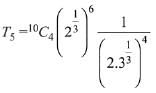
and 5th term from end T11-5+1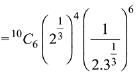
∴ T5 : T7 =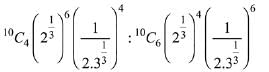
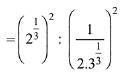
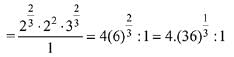
Q.17. The total number is irrational terms in the binomial expansion of 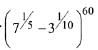 is: (2019)
is: (2019)
(1) 55
(2) 49
(3) 48
(4) 54
Ans. (4)
Solution. Let the general term of the expansion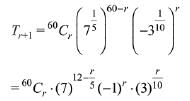
Then, for getting rational terms, r should be multiple of L.C.M. of (5, 10)
Then, r can be 0, 10, 20, 30, 40, 50, 60.
Since, total number of terms = 61
Hence, total irrational terms = 61 - 7 = 54
Q.18. The sum of the co-efficients of all even degree terms in x in the expansion of 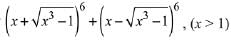 is equal to: (2019)
is equal to: (2019)
(1) 29
(2) 32
(3) 26
(4) 24
Ans. (4)
Solution.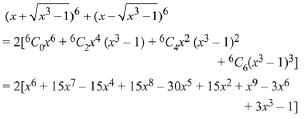
Hence, the sum of coefficients of even powers of
x = 2[1 - 15 + 15 + 15 - 3- 1] = 24
Q.19. The sum of the series 2.20C0 + 5.20C1 + 8.20C2 + 11.20C3 + ... + 62.20C20 is equal to: (2019)
(1) 226
(2) 225
(3) 223
(4) 224
Ans. (2)
Solution.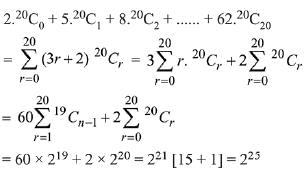
Q.20. If the fourth term in the binomial expansion of 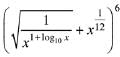 is equal to 200, and x > 1, then the value of x is: (2019)
is equal to 200, and x > 1, then the value of x is: (2019)
(1) 100
(2) 10
(3) 103
(4) 104
Ans. (2)
Solution. The fourth term is equal to 200.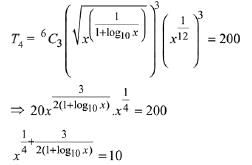
Taking log10 on both sides and putting log10 x = t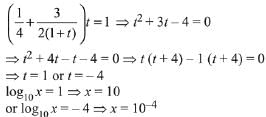
According to the question x > 1, ∴ x = 10.
Q.21. If the fourth term in the Binomial expansion of  is 20 x 87, then a value of x is: (2019)
is 20 x 87, then a value of x is: (2019)
(1) 83
(2) 82
(3) 8
(4) 8-2
Ans. (2)
Solution.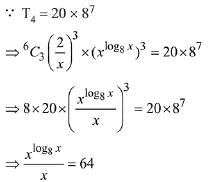
Now, take log8 on both sides, we get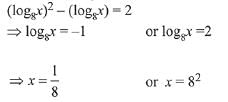
Q.22. If some three consecutive coefficients in the binomial expansion of (x+1)n in powers of x are in the ratio 2:15:70, then the average of these three coefficients is: (2019)
(1) 964
(2) 232
(3) 227
(4) 625
Ans. (2)
Solution.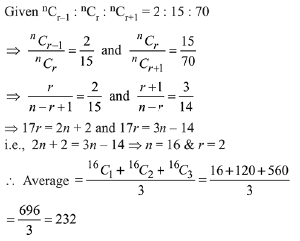
Q.23. If the coefficients of x2 and x3 are both zero, in the expansion of the expression (1 + ax + bx2) (1-3x)15 in powers of x, then the ordered pair (a, b) is equal to: (2019)
(1) (28,861)
(2) (-54,315)
(3) (28,315)
(4) (-21,714)
Ans. (3)
Solution. Given expression is 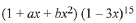
Co-efficient of x2 = 0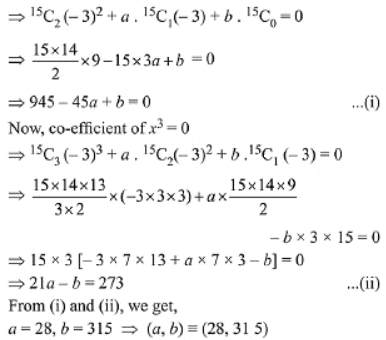
Q.24. The smallest natural number n, such that the coefficient of x in the expansion of 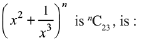 (2019)
(2019)
(1) 38
(2) 58
(3) 23
(4) 35
Ans. (1)
Solution.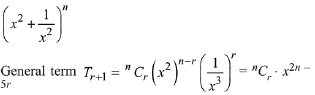
To find coefficient of x, 2n - 5r = 1
Given nCr = nC23 ⇒ r = 23 or n - r = 23
∴ n = 58 or n = 38
The minimum value is n = 38
Q.25. The coefficient of x18 in the product (1+x)(1-x)10(1+x+x2)9 is: (2019)
(1) 84
(2) -126
(3) -84
(4) 126
Ans. (1)
Solution. Given expression,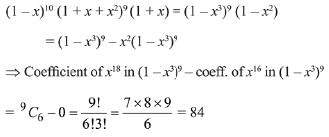
Q.26. If 20C1 + (22) 20C2 +(32) 20C3+ ...... + (202) 20C20= A(2β), then the ordered pair (A, P) is equal to: (2019)
(1) (420, 19)
(2) (420, 18)
(3) (380,18)
(4) (380, 19)
Ans. (2)
Solution.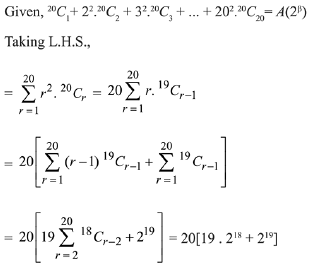
=420 x 218
Now, compare it with R.H.S., A = 420 and β = 18
Q.27. The term independent of x in the expansion of 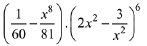 is equal to: (2019)
is equal to: (2019)
(1) - 72
(2) 36
(3) - 36
(4) - 108
Ans. (4)
Solution. Given expression is,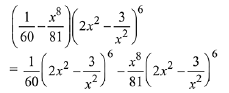
Term independent of x,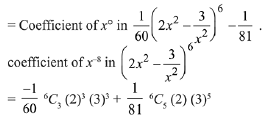
= -72+ 36 = -36
Q.28. The sum of the coefficients of all odd degree terms in the expansion of 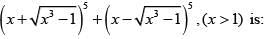 (2018)
(2018)
(1) -1
(2) 0
(3) 1
(4) 2
Ans. (4)
Solution.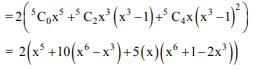
Sum of coefficient of odd powers = 2(1 - 10 + 10) = 2.
Q.29. If n is the degree of the polynomial 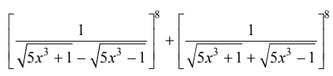 and m is the coefficient of xn in it, then the ordered pair (n,m) is (2018)
and m is the coefficient of xn in it, then the ordered pair (n,m) is (2018)
(1) (12, (20)4)
(2) (8, 5(10)4)
(3) (24, (10)8)
(4) (12, 8(10)4)
Ans. (4)
Solution. 
After rationalizing the polynomial, we get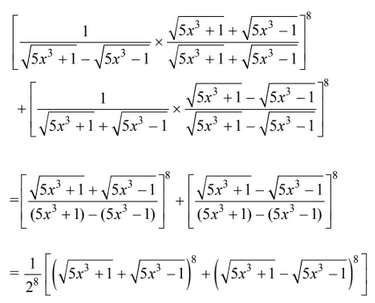
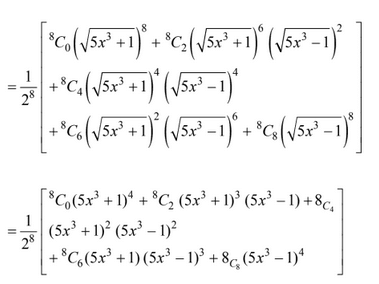
So, the degree of the polynomial is 12,
No, thew coefficient of x12 is 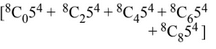
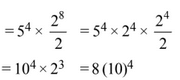
Q.30. The coefficient of x2 in the expansion of the product (2 - x2) · ((1 + 2x + 3x2)6 + (1 - 4x2)6) is: (2018)
(1) 107
(2) 108
(3) 155
(4) 106
Ans. (4)
Solution. (a) Let a = ((1 + 2x + 3x2)6 + (1 - 4x2)6)
∴ Coefficient of x2 in the expansion of the product
(2 - x2) ((1 + 2x + 3x2)6+ (1 - 4x2)6)
= 2 (Coefficient of x2 in a) - 1 (Constant of expansion)
In the expansion of ((1 + 2x + 3x2)6 + (1 - 4x2)6).
Constant = 1 + 1 = 2
Coefficient of x2 = [Coefficient of x2 in (6C0(1 + 2x)6(3x2)0)] + [Cofficient of x2 in (6C1(1 + 2x)5 (3x2)1)] - [6C1 (4x2)] = 60 + 6 x 3 - 24 = 54
∴ The coefficient of x2 in (2 - x2)((1 + 2x + 3x2)6+ (1 - 4x2)6)
=2 x 54 - 1 (2)= 108 - 2 = 106
Q.31. The value of (21C1 - 10C1) + (21C2 - 10C2) + (21C3 - 10C3) + (21C4 - 10C4) + ... + (21C10 - 10C10) is: (2017)
(1) 220 – 210
(2) 221 – 211
(3) 221 – 210
(4) 220 – 29
Ans. (1)
Solution. 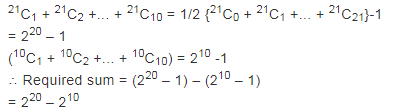
Q.32. If (27)999 is divided by 7, then the remainder is: (2017)
(1) 3
(2) 1
(3) 6
(4) 2
Ans. (3)
Solution.
Simplify the Base:
- First, divide 27 by 7.
- 27 divided by 7 is 3 with a remainder of 6.
- This means 27 leaves the same remainder as 6 when divided by 7.
- So, instead of calculating 27⁹⁹⁹, you can work with 6⁹⁹⁹.
Identify the Pattern in Powers of 6:
Calculate the first few powers of 6 and find their remainders when divided by 7.
- 6¹ is 6. When divided by 7, the remainder is 6.
- 6² is 36. When divided by 7, the remainder is 1.
- 6³ is 216. When divided by 7, the remainder is 6.
- 6⁴ is 1296. When divided by 7, the remainder is 1.
Pattern Observed: The remainders alternate between 6 and 1 every power.
Determine the Position in the Pattern:
- The pattern repeats every 2 powers.
- Since 999 is an odd number, it corresponds to the first position in the pattern.
- Therefore, the remainder for 6⁹⁹⁹ divided by 7 is the same as the remainder for 6¹, which is 6.
- The remainder when 27⁹⁹⁹ is divided by 7 is 6.
Q.33. The coefficient of x-5 in the binomial expansion of 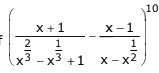 where x ≠ 0, 1 is: (2017)
where x ≠ 0, 1 is: (2017)
(1) -1
(2) 4
(3) 1
(4) -4
Ans. (3)
Solution.
Since a3+1 = (a+1)(a2-a+1)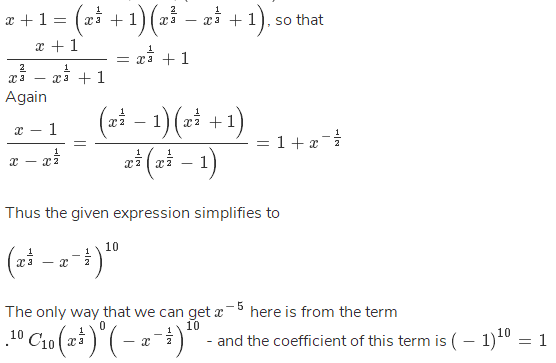
Q.34. If the number of terms in the expansion of 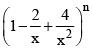 , x ≠ 0, is 28, then the sum of the coefficients of all the terms in this expansion, is: (2016)
, x ≠ 0, is 28, then the sum of the coefficients of all the terms in this expansion, is: (2016)
(1) 64
(2) 2187
(3) 243
(4) 729
Ans. (4)
Solution. Total number of terms = n+2C2 = 28
⇒(n+2)(n+1) = 56
⇒ n=6
Sum of coefficients =(1-2+4)n = 36 = 729
Q.35. The value of 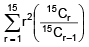 is equal to: (2016)
is equal to: (2016)
(1) 1085
(2) 560
(3) 680
(4) 1240
Ans. (3)
Solution. 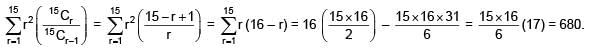
Q.36. For x ∈ R, x ≠ –1, if (1 + x)2016 + x (1 + x)2015 + x2 (1 + x)2014 + …….. + x2016 =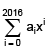 ,then a17 is equal to: (2016)
,then a17 is equal to: (2016)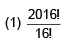
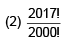

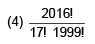
Ans. (3)
Solution. 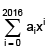 =
=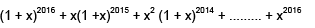

Q.37. 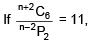 then n satisfies the equation (2016)
then n satisfies the equation (2016)
(1) n2 + n – 110 = 0
(2) n2 + 5n – 84 = 0
(3) n2 + 3n – 108 = 0
(4) n2 + 2n – 80 = 0
Ans. (3)
Solution.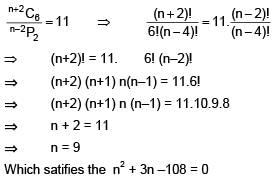
Q.38. If the coefficients of x–2 and x–4 in the expansion of 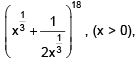 are m and n respectively, then m/n is equal to: (2016)
are m and n respectively, then m/n is equal to: (2016)
(1) 5/4
(2) 4/5
(3) 27
(4) 182
Ans. (4)
Solution.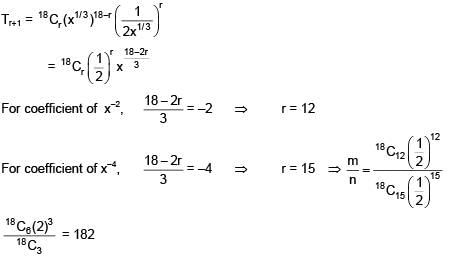
FAQs on JEE Main Previous year questions: Mathematical Induction and Binomial Theorem
| 1. What is the principle of mathematical induction and how is it applied in JEE Main questions? |  |
| 2. How can the Binomial Theorem be used to expand expressions in JEE Main? |  |
| 3. What are some common types of problems related to mathematical induction seen in JEE Main? |  |
| 4. Can you provide an example of a Binomial Theorem problem from previous JEE Main papers? |  |
| 5. How important is the understanding of mathematical induction and Binomial Theorem for JEE Main preparation? |  |














