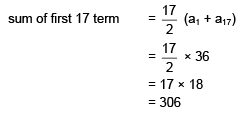JEE Main Previous Year Questions (2016- 2025): Sequences and Series PDF Download

Q.1. Five numbers are in A.P., whose sum is 25 and product is 2520. If one of these five numbers is -1/2, then the greatest number amongst them is    (2020)
(1) 27
(2) 7
(3) 21/2
(4) 16
Ans. (4)
Solution. Let the five terms of A.P. be a - 2d, a - d, a, a + d and a + 2d.
Therefore,
a - 2d + a - d + a + a + d + a + 2d = 25
⇒ 5a = 25 ⇒ a = 5
Now, (a - 2d)(a - d)a(a + d)(a + 2d) = 2520
⇒ (a² - 4d²) (a² - d²) = 504
⇒ (25 - 4d²)(25 - d²) = 504
⇒ 4d² - 125d² + 121 = 0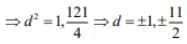

Now, none of the term of A.P. is -1/2 by using d = ±1. So, d = ± 11/2
So, the terms of A.P. are -6, -1/2, 5, 21/2 and 16. Hence, the greatest term among them is 16.

Q.2. Let a₁, a₂, a₃,… be a G.P. such that a₁ < 0, a₁ + a₂ = 4 and a₃ + a₄ = 16. If 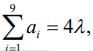 then λ is equal to    (2020)
(1) -513
(2) -171
(3) 171
(4) 511/3
Ans. (2)
Solution. Let the common ratio of G.P. be r, then
a₁ + a₂ = 4 ⇒ a₁ + a₁r = 4
⇒ a₁(1 + r) = 4 ...(1)
And
a₃ + a₄ = 16 ⇒ a₁r² + a₁r³ = 16
⇒ a₁r²(r+1) = 16 ...(2)
From Eqs. (1) and (2), we get
r² = 4 ⇒ r = -2 (since a₁ < 0)
Now,
a₁ + a₂ = 4 ⇒  a₁(1 + r) = 4 ⇒ a₁ = -4
Therefore,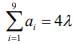




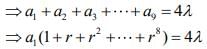
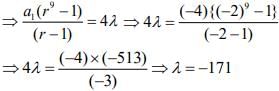
Q.3. If a, b and c be three distinct real numbers in G.P. and a + b + c = xb, then x cannot be:    (2019)
(1) -2    
(2) -3
(3) 4    
(4) 2
Ans. (4)
Solution. 
∵ a, b, c, are in G.P.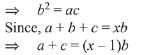

Take square on both sides, we get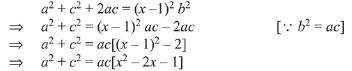

∵ a² + c² is positive and b² = ac which is also positive.
Then, x² - 2x - 1 would be positive but for x = 2, x² - 2x - 1 is negative.
Hence, x cannot be taken as 2.

Q.4. Let a₁, a₂, ..... a₃₀ be an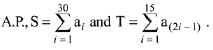  
If a₅ = 27 and S - 2T = 75, then a₁₀ is equal to:    (2019)
(1) 52    
(2) 57
(3) 47    
(4) 42
Ans. (1)
Solution.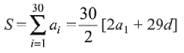 


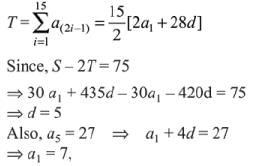
Hence, a₁₀ = a₁ + 9d = 7 + 9 x 5 = 52

Q.5. The sum of the following series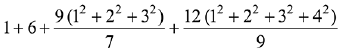

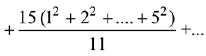 up to 15 terms, is:    (2019)
(1) 7520    
(2) 7510
(3) 7830    
(4) 7820
Ans. (4)
Solution.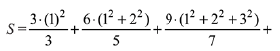

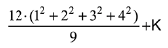
Now, n^th term of the series,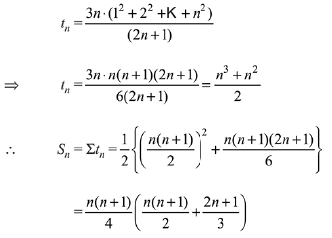

Hence, sum of the series up to 15 terms is,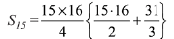


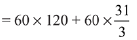
= 7200 + 620
= 7820

Q.6. Let a, b and c be the 7^th, 11^th and 13^th terms respectively of a non-constant A.P. If these are also the three consecutive terms of a G.P., then a/c is equal to:    (2019)
(1) 2    
(2) 1/2
(3) 7/13
(4) 4
Ans. (4)
Solution. Let first term and common difference be A and D respectively.
∴ a = A + 6D, b = A+ 10D and c = A + 12D
Since, a, b, c are in G.P.
Hence, relation between a, b and c is,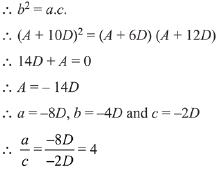


Q.7. Let a₁, a₂, a₃, ..... a₁₀ be in G.P. with a_i > 0 for i = 1,2, .... 10 and S be the set of pairs (r,k), r,k ∈ N (the set of natural numbers) for which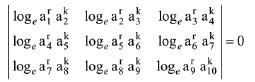

Then the number of elements in S, is:    (2019)
(1) 4    
(2) infinitely many
(3) 2    
(4) 10
Ans. (2)
Solution. Let common ratio of G.P. be R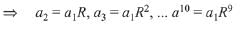

C1→ C1-C2, C2→ C2-C3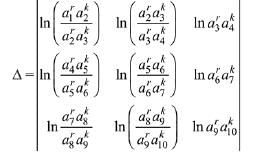


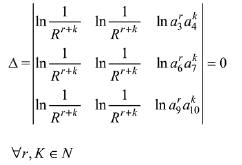
Hence, number of elements in S is infinitely many.

Q.8. The sum of an infinite geometric series with positive terms is 3 and the sum of the cubes of its terms is 27/19. Then the common ratio of this series is:    (2019)
(1) 1/3    
(2) 2/3
(3) 2/9    
(4) 4/9
Ans. (2)
Solution. Let the terms of infinite series are a, ar, ar², or³, ...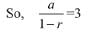

 Since, sum of cubes of its terms is 27/19 that is sum of a³, a³r³....

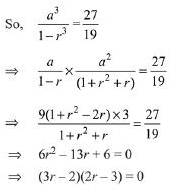
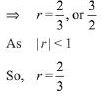
Q.9. Let a₁, a₂, ..., be a G.P. If 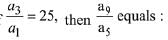    (2019)
(1) 5⁴    
(2) 4(5²)
(3) 5³    
(4) 2(5²)
Ans. (1)
Solution. Let a₁ = a, a₂ = ar, a₃ = ar² ... a₁₀ = ar⁹
where r= common ratio of given G.P.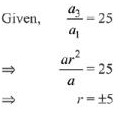

Now,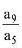  

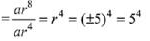
Q.10. Let α and β be the roots of the quadratic equation x² sinθ -x (sinθ cosθ + 1) + cosθ = 0 (0 < θ < 45°), and 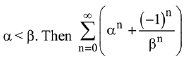 is equal to:    (2019)
(1)
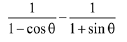
(2)
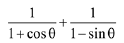
(3)
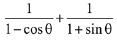
(4)
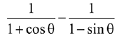
Ans. (3)
Solution.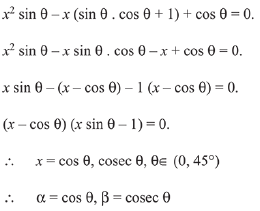



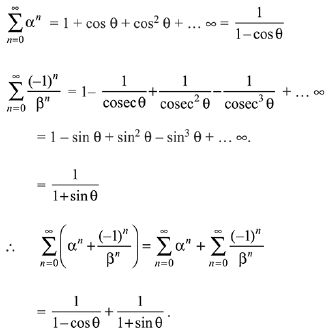
Q.11. If 19th term of a non-zero A.P. is zero, then its (49th term): (29th term) is:    (2019)
(1) 4:1    
(2) 1:3
(3) 3:1    
(4) 2:1
Ans. (3)
Solution. Let first term and common difference of AP be a and d respectively, then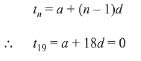

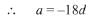   ...(1)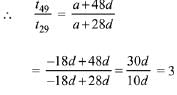

t₄₉ : t₂₉ =  3 : 1

Q.12. The product of three consecutive terms of a G.P. is 512. If 4 is added to each of the first and the second of these terms, the three terms now form an A.P. Then the sum of the original three terms of the given G.P. is:    (2019)
(1) 36    
(2) 32
(3) 24    
(4) 28
Ans. (4)
Solution. Lets three terms of a G.P. be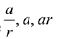

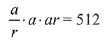
a³ = 512
a = 8
4 is added to each of the first and the second of three terms then three terms are,
 


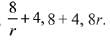
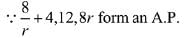
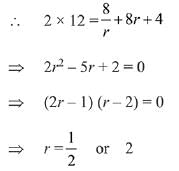
Therefore, sum of three terms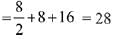

Q.13. 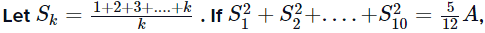Then A is equal to    (2019)
(1) 283    
(2) 301
(3) 303    
(4) 156
Ans. (3)
Solution.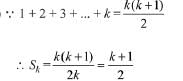




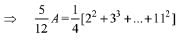
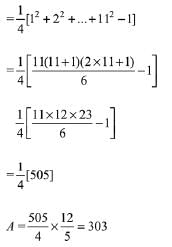
Q.14. If ⁿC₄, ⁿC₅ and ⁿC₆ are in A.P., then n can be:    (2019)
(1) 9    
(2) 14
(3) 11    
(4) 12
Ans. (2)
Solution. Since ⁿC₄, ⁿC₅ and ⁿC₆ are in A.P.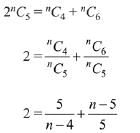



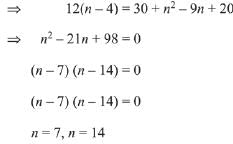
Q.15. If the sum of the first 15 terms of the series 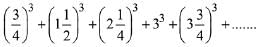 is equal to 225 k then k is equal to:    (2019)
(1) 108    
(2) 27
(3) 54    
(4) 9
Ans. (2)
Solution.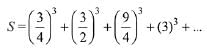


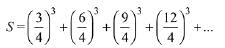
Let the general term of S be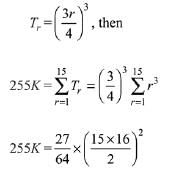

⇒ k = 27

Q.16. If three distinct numbers a, b, c are in G.P. and the equations ax² + 2bx + c = 0 and dx² + 2ex + f = 0 have a common root, then which one of the following statements is correct?    (2019)
(1)
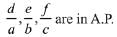
(2) d, e, f are in A.P.
(3) d, e, f are in G.P.
(4)
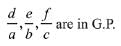
Ans. (1)
Solution. Since a, b, c are in G.P.
∴ b² = ac
Given equation is, ax² + 2bx + c = 0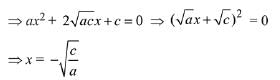

Also, given that ax² + 2bx + c = 0 and dx² + 2ex + f = 0 have a common root.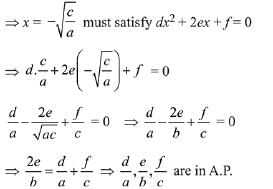


Q.17. The sum 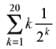 is equal to:    (2019)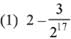




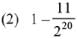
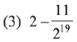
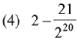
Ans. (3)
Solution.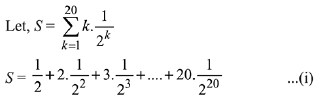 


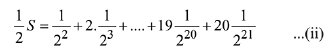
On subtracting equations (ii) by (i),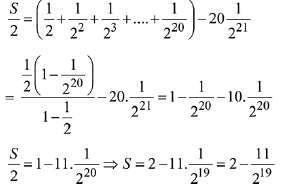


Q.18. Let the sum of the first n terms of a non-constant A.P., a₁, a₂, a₃, ..... be 50n + 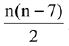 A, where A is a constant. If d is the common difference of this A.P., then the ordered pair (d, a₅₀) is equal to:    (2019)
(1) (50.50 + 46A)    
(2) (50, 50 + 45A)
(3) (A, 50 + 45A)    
(4) (A, 50 + 46A)
Ans. (4)
Solution.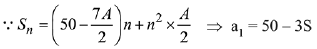





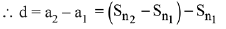
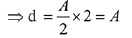
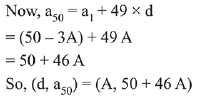
Q.19. If the sum and product of the first three terms in an A,P. are 33 and 1155, respectively, then a value of its 11^th term is:    (2019)
(1) -35    
(2) 25    
(3) -36    
(4) -25
Ans. (4)
Solution. Let three terms of A.P. are a - d, a, a + d
Sum of terms is, a - d + a + a + d = 33 ⇒ a = 11
Product of terms is, (a - d)a(a + d)= 11(121 -d²)= 1155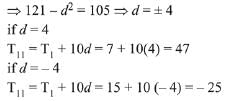


Q.20. The sum of the series 1+ 2 x 3+ 3 x 5 + 4 x 7 + ..... up to 11^th term is:    (2019)
(1) 915    
(2) 946    
(3) 945    
(4) 916
Ans. (2)
Solution.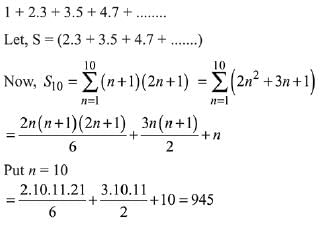

Hence required sum of the series = 1 + 945 = 946

Q.21. If a₁, a₂, a₃, ... an are in A.P. and a₁ + a₄ + a₇ + ....+ a₁₆ = 114, then a₁ + a₆ + a₁₁ + a₁₆ is equal to:    (2019)
(1) 98    
(2) 76    
(3) 38    
(4) 64
Ans. (2)
Solution.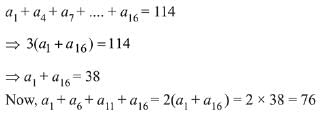


Q.22. The sum 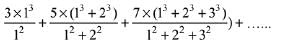 up to 10^th term, is:    (2019)
(1) 680    
(2) 600    
(3) 660    
(4) 620
Ans. (3)
Solution.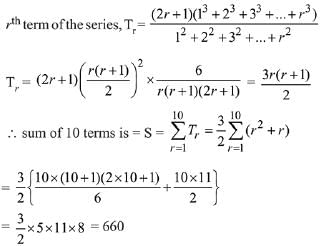


Q.23. The sum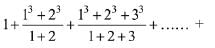 

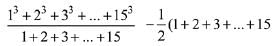 is equal to:    (2019)
(1) 620    
(2) 1240    
(3) 1860    
(4) 660
Ans. (1)
Solution.


Q.24. Let a, b and c be in G.P. with common ratio r, where a≠ 0 and 0 < r≤ 1/2. If 3a, 7b and 15c are the first three terms of an A.P., then the 4^th term of this A.P. is:    (2019)
(1) 2/3a
(2) 5a
(3) 7/3a
(4) a
Ans. (4)
Solution. ∵ a, b, c are in G.P. ⇒ b = ar, c = ar²
∵ 3a, 7b, 15c are in A.P. ⇒ 3a, 7ar, 15ar² are in A.P.
∴ 14ar = 3a + 15 ar²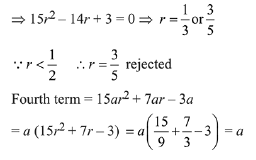


Q.25. For x ∈ R, let [x] denote the greatest integer ≤ x, then the sum of the series 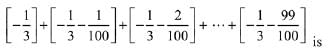    (2019)
(1) -153    
(2) -133    
(3) -131    
(4) -135
Ans. (2)
Solution.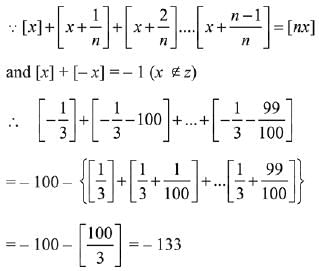


Q.26. If α and β are the roots of the equation 375x²-25x-2=0, 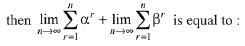    (2019)
(1) 21/346
(2) 29/358
(3) 1/12
(4) 7/116
Ans. (3)
Solution. 

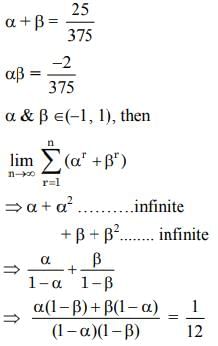
Q.27. Let S_n denote the sum of the first n terms of an A.P.
If S₄ = 16 and S₆ = -48, then S₁₀ is equal to:    (2019)
(1) -260    
(2) -410    
(3) -320    
(4) -380
Ans. (3)
Solution.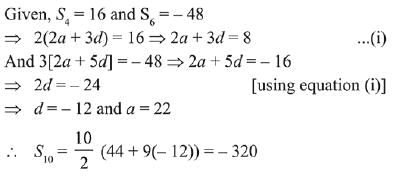


Q.28. If a₁, a₂, a₃, .... are in A.P. such that a₁ + a₇ + a₁₆ = 40, then the sum of the first 15 terms of this A.P. is:    (2019)
(1) 200    
(2) 280    
(3) 120    
(4) 150
Ans. (1)
Solution. Let the common difference of the A.P. is ‘d’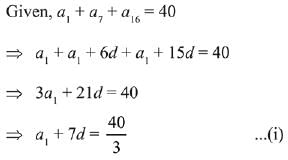

Now, sum of first 15 terms of this A.P. is,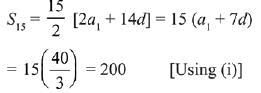


Q.29. If α, β and γ are three consecutive terms of a non-constant G.P. such that the equations ax²+2βx+γ =0 and x²+x-1=0 have a common root, then α (β+γ) is equal to:    (2019)
(1) 0    
(2) αβ
(3) αγ
(4) βγ
Ans. (4)
Solution. 
∵ α, β, γ are three consecutive terms of a non-constant G.P.
∴ β² = αγ
So roots of the equation ax² +2βx + γ = 0 are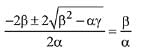

∵ ax² + 2βx + γ = 0 and x² + x - 1 = 0 have a common root.
∴ this root satisfy the equation x² + x - 1 = 0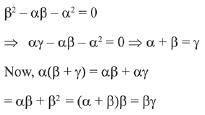


Q.30. Let a₁ , a₂ , a₃ , ......, a49 be in A.P. such that 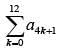 = 416 a₉ + a₄₃  = 66.
If a₁² + a₂² + .... + a₁₇² = 140m then m is equal to:    (2018)
(1) 66
(2) 68
(3) 34
(4) 33
Ans. (3)
Solution. a₁ + a₅ + a₉ = 416 ⇒ a + 24d = 32 ......(i)
a₉ + a₄₃ = 66 ⇒ a + 25d = 33......(ii)
From (i) and (ii) d = 1 and a = 8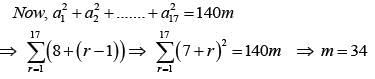


Q.31. If x₁ , x₂ …. , x_n and 1/h₁, 1/h₂ ...... 1/h_n are two A. P.s such that x₃ = h₂ = 8 and x₈ = h₇ = 20 , then x₅ . h₁₀ equals:    (2018)
(1) 2650
(2) 2560
(3) 3200
(4) 1600
Ans. (2)
Solution.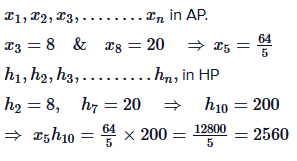 


Q.32. If b is the first term of an infinite G.P. whose sum is five, then b lies in the interval:    (2018)
(1) (0, 10)
(2) [10, ∞]
(3) (-10, 0)
(4) (-∞, -10]
Ans. (1)
Solution. If b is the first term and r is the common ratio of an infinite G.P. then sum is 5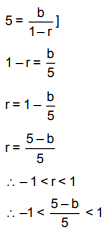

– 5 < 5 – b < 5
– 5 < 5 – b < 5
– 10 < – b < 0
0 < b < 10
b ∈ (0,10)

Q.33. Let 1/x₁, 1/x₂ ,..., 1/x_n (x_i ≠ 0 for i = 1, 2, & ., n) be in A.P. such that x₁ = 4 and x₂₁ = 20. If n is the least positive integer for which x_n > 50, then 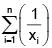 is equal to:    (2018)
(1) 3
(2) 1/8
(3) 13/4
(4) 13/8
Ans. (3)
Solution.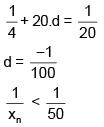



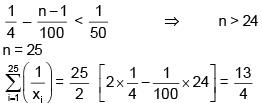
Q.34. The sum of the first 20 terms of the series 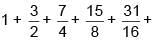 ..... is:    (2018)
(1)
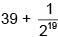
(2)
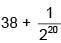
(3)
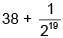
(4)
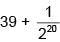
Ans. (3)
Solution.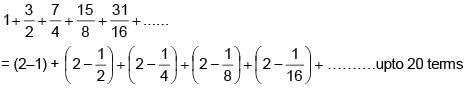



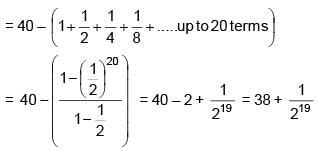
Q.35. For any three positive real numbers a, b and c, 9(25a² +b²)+ 25(c² - 3ac) = 15b(3a + c). Then    (2017)
(1) a, b and c are in G.P
(2) b, c and a are in G.P
(3) b, c and a are in A.P
(4) a, b and c are in A.P
Ans. (3)
Solution. 9(25a² + b²) + 25 (c² - 3ac) = 15b (3a + c)
⇒ (15a)² + (3b)² + (5c)² - 45ab - 15bc - 75ac = 0
⇒ (15a - 3b)² + (3b - 5c)² + (15a - 5c)² = 0
It is possible when
15a - 3b = 0 and 3b - 5c = 0 and 15a - 5c= 0
15a = 3b= 5c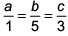

∴ b, c, a are in A.P.

Q.36. Let a, b, c ∈ R. If f(x) = ax² + bx + c is such that a + b + c = 3 and 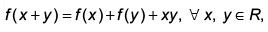then 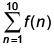 is equal to    (2017)
(1) 255
(2) 330
(3) 165
(4) 190
Ans. (2)
Solution. As, f (x + y)= f (x) + f (y) + xy
Given, f (1) = 3
Putting, x = y = 1 ⇒ f (2) = 2f (1)+ 1 = 7
Similarly, x = 1,y = 2 ⇒ f (3) = f (1) + f (2) + 2 = 12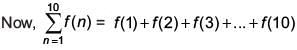

= 3 + 7 + 12 + 18 + ... = S (let)
Now, S = 3 + 7 + 12 + 18 + ... +t_n
Again, S = 3 +7 + 12 + ... +t_{n -1} + t_n
We get, t_n = 3 + 4 + 5 + ... terms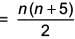






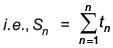
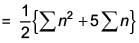
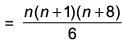
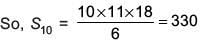
Q.37. If the arithmetic mean of two numbers and b,a, > b > 0. is five times their geometric mean, then 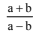 is equal to:    (2017)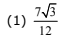




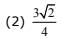
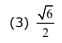
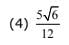
Ans. (4)
Solution.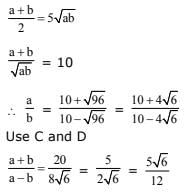


Q.38. If the sum of the first n terms of the series 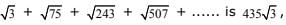then n equals:    (2017)
(1) 13
(2) 15
(3) 29
(4) 18
Ans. (2)
Solution.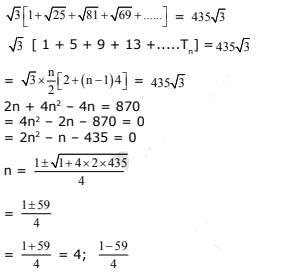


Q.39. If three positive numbers a, b and c are in A.P. such that abc = 8, then the minimum possible value of b is:    (2017)
(1) 4^2/3 
(2) 2
(3) 4^1/3
(4) 4
Ans. (2)
Solution. 
For a set of positive numbers, the arithmetic mean is never smaller than the geometric mean. The geometric mean of the three numbers is 3 √ 8 = 2 . Since the numbers are in AP, their arithmetic mean is b . Thus the smallest possible value for b is 2 (this is achievable when all three numbers are 2 - an AP with zero common difference)

Q.40. Let  then n is equal to:    (2017)
(1) 200
(2) 199
(3) 99
(4) 19
Ans. (2)
Solution.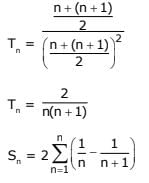


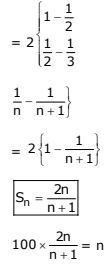
n + 1 = 200
n = 199

Q.41. If the sum of the first ten terms of the series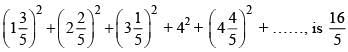m, then m is equal to:    (2016)
(1) 102
(2) 101
(3) 100
(4) 99
Ans. (2)
Solution.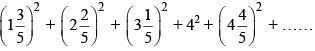
upto 10 terms
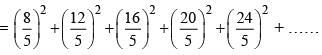upto 10 terms.
(8)² + (12)² + (16)² + ……… up to 10 terms
T_n = [4 (n + 1)]² where n varies from 1 to 10.
= 16(n² + 2n + 1)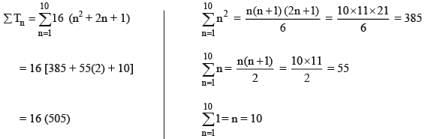

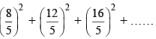upto 10 terms=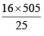
It is given that 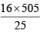= 16/5 m
∴ m = 505/5 = 101

Q.42. If the 2^nd, 5^th and 9^th terms of a non-constant A.P. are in G.P., then the common ratio of this G.P. is:    (2016)
(1) 8/5
(2) 4/3
(3) 1
(4) 7/4
Ans. (2)
Solution. t₂ = a + d
t₅ = a + 4d
t₉ = a + 8d
Given  t₂, t₅, t₉ are in G.P.
(a + 4d)² = (a + d) (a + 8d)
a² + 16d² + 8ad = a² + 8d² + 9ad
8d² - ad = 0
d(8d - a) = 0
As given non-constant AP. => d ≠ 0
∴ d = a/8 => a = 8d
so,  A.P. is  8d, 9d, 10d, …..
Common ratio of G.P. =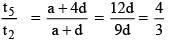

Q.43. Let x, y, z be positive real numbers such that x + y + z = 12 and x³y⁴z⁵ = (0.1) (600)³. Then x³ + y³ + z³ is equal to    (2016)
(1) 270
(2) 258
(3) 216
(4) 342
Ans. (3)
Solution. x + y + z = 12
x³y⁴ z⁵ = (0.1) (600)³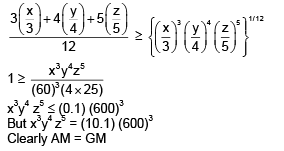 



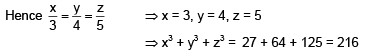
Q.44. The sum 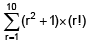 is equal to    (2016)
(1) 10 × (11!)
(2) 101 × (10!)
(3) (11!)
(4) 11 × (11!)
Ans. (1)
Solution.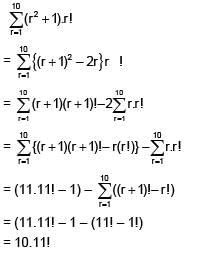


Q.45. Let a₁, a₂, a₃,......., a_n ,.......be in A.P. If a₃ + a₇+ a₁₁+ a₁₅ = 72 then the sum of its first 17 terms is equal to    (2016)
(1) 153
(2) 306
(3) 612
(4) 204
Ans. (2)
Solution. a₁, a₂, a₃,......., a_n ,....... are in A.P.
a₃ + a₁₅ = a₇ + a₁₁ = a₁ + a₁₇ = 36