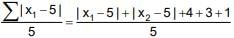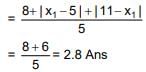Previous year questions (2016-2025): Miscellaneous (Sets, Relations, Statistics & Mathemati | JEE Main PDF Download

Q.1. The logical statement (p ⇒ q) ∧ ( q ⇒~ p) is equivalent to    (2020)
(1) p
(2) q
(3) ~p
(4) ~ q
Ans. (3)
We have
(p → q) ∧ (q → -p)
≡ (∼p ∨ q) ∧ (∼qv ∼ p)
≡ ∼ p ∨ (q ∧ ∼ q) ≡ ∼ p ∨ C ≡ ∼p

Q.2. Let A, B, C and D be four non-empty sets. The contrapositive statement of “If A ⊆ B and B ⊆ D, then A ⊆ C" is    (2020)
(1) If 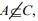 then A ⊆ B and B ⊆ D
(2) If A ⊆ C, then B ⊂ A and D ⊂ B
(3) If 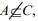 then 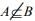 and B ⊆ D
(4) 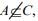 then 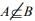 and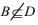
Ans. (4)
The contrapositive of p → q is - q → - p.
Now,

 
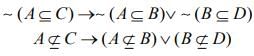
Q.3. Which one of the following is a tautology?    (2020)
(1) P ∧ (P → Q) → Q
(2) Q → (P ∧ (P → Q))
(3) P ∧ (P ∨ Q)
(4) P ∨ (P ∧ Q)
Ans. (1)
We have
(1) P ∧ (P → Q) → Q ≡ (P ∧ (- P ∨ Q)) → Q ≡ (P ∧ Q) → Q
≡ ((∼P) ∨ (∼Q)) ∨ Q ≡ (∼P) ∨ t ≡ t
(2) Q → (P ∧ (P → Q)) ≡ Q → (P ∧ (-P ∨ Q)) ≡ Q → (P ∧ Q) ≡ (-Q) ∨ (P ∧ Q) ≡ (P ∨ (-Q))
(3) P ∧ (P ∨ Q) ≡ P
(4) P ∨ (P ∧ Q) = P

Q.4. Which of the following statements is a tautology?    (2020)
(1) p ∨ (∼q) → p ∧ q
(2) ∼ (p ∧ ∼ q) → p ∨ q
(3) ∼ (p ∨ ∼ q) → p ∧ q
(4) ∼ (p ∨ ∼ q) → p ∨ q
Ans. (4)
We have
- (p ∨ - q) → p ∨ q
≡ - (p ∧ q) → p ∨ q ≡ - {(-p ∧ q) ∧ (- p∧ - q)}
≡ -(- p ∧ f)

Q.5. Negation of the statement: ‘√5 is an integer or 5 is irrational’ is    (2020)
(1) √5 is not an integer or 5 is not irrational.
(2) √5 is not an integer and 5 is not irrational.
(3) √5 is irrational or 5 is an integer.
(4) √5 is integer and 5 is irrational.
Ans. (2)
We have  -(p ∨ q) = - p∧ - q
Hence, the Negation of the statement: '√5 is an integer or 5 is irrational’ is “√5 is not an integer and 5 is not irrational.”

Q.6. If p → (p∧ ∼ q) is false, then the truth values of p and q are respectively    (2020)
(1) F, F
(2) T, F
(3) T, T
(4) F, T
Ans. (3)
We have

Hence, p → (p → p∧ ∼ q) is false when the truth values of p and q are T, T respectively.

Q.7. If the variance of the first n natural numbers is 10 and the variance of the first m even natural numbers is 16, then m + n is equal to ________.    (2020)
Ans. (18.00)
The variance of first n natural number is given by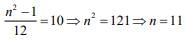

The variance of first m even natural number is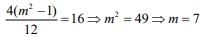

Hence, m + n = 11 + 7 = 18

Q.8. If the mean and variance of eight numbers 3, 7, 9, 12, 13, 20, x and y be 10 and 25 respectively, then x . y is equal to _______.    (2020)
Ans. (54.00)
The mean of eight numbers 3, 7, 9, 12, 13, 20, x and y be 10 , then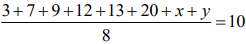

⇒ x + y = 80 - 64 = 16 ...(1)
The variance of eight numbers 3, 7, 9, 12, 13, 20, x and y be 25, then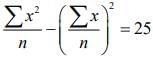


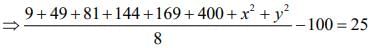
⇒ x² + y² = 1000 - 852 = 148 ...(2)
From Eqs. (1) and (2), we get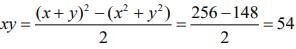


Q.9. The mean and the standard deviation (s.d.) of 10 observations are 20 and 2 respectively. Each of these 10 observations is multiplied by p and then reduced by q, where p ≠ 0 and q ≠ 0. If the new mean and new s.d. become half of their original values, then q is equal to    (2020)
(1) −5
(2) 10
(3) −20
(4) −10
Ans. (3)
If each observation is multiplied with p and then reduced by q, then
New mean,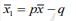
⇒ 20p - q = 10 ...(1)
and new standard deviation is given by σ₂ = |p|σ₂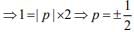
 ...(2)
From Eqs. (1) and (2), we get
p = -1/2 and - 10 - q = 10 ⇒ q = -20

Q.10. The mean and variance of 20 observations are found to be 10 and 4, respectively. On rechecking, it was found that an observation 9 was incorrect and the correct observation was 11. Then, the correct variance is    (2020)
(1) 3.99
(2) 4.01
(3) 4.02
(4) 3.98
Ans. (1)
We have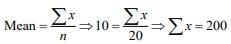
 ...(1)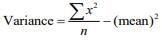

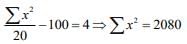 ...(2)
Now,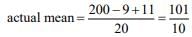


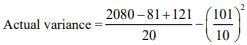
= 106 - 102.1 = 3.99

Q.11. Let the observations x(1 ≤ i ≤ 10)  satisfy the equations 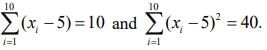If μ and λ are the mean and the variance of the observations, x₁ - 3, x₂ - 3, .... ,x₁₀ - 3, then the ordered pair (μ, λ) is equal to    (2020)
(1) (3, 3)
(2) (6, 3)
(3) (6, 6)
(4) (3, 6)
Ans. (1)
Given,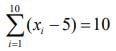


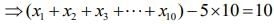
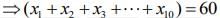 ...(1)
Again, we have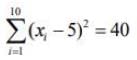


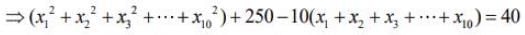
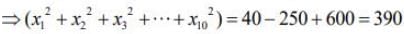...(2)
Now, the mean of x₁ - 3, x₂ - 3, .... , x₁₀ - 3 is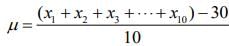


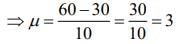
The variance of x₁ - 3, x₂ - 3, .... , x₁₀ - 3 is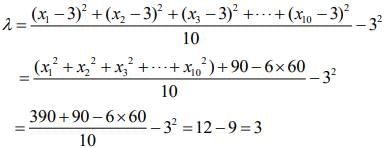


Q.12. Let 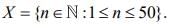 If A = {n ∈ X : n is a multiple of 2} and B = {n ∈ X : n is a multiple of 7}, then the number of elements in the smallest subset of X containing both A and B is _______.    (2020)
Ans. (29.00)
Number of elements in set A, n (A) = 25
Number of elements in set B, n (B) = 7
Number of common elements in both the sets, n (A ∩ B) = 3
Hence, number of elements in the smallest subset of X containing both A and B is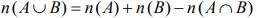

= 25 + 7 - 3 = 29

Q.13. Let S be the set of all real roots of the equation, 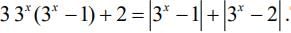 Then, S    (2020)
(1) Contains exactly two elements.
(2) Is a singleton.
(3) Is an empty set.
(4) Contains at least four elements.
Ans. (2)
We have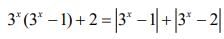

Let 3^x = t, then t(t - 1) + 2 = |t - 1| + |t - 2|
⇒ t² - t + 2 = |t - 1|+ |t - 2| ...(1)
Case 1: When t < 1, then
t² - t + 2 = 1 - t + 2 - t ⇒ t² + t - 1 = 0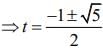

Hence, only 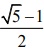 is only acceptable value.
Case 2: When 1 ≤ t < 2, then
t² - t + 2 = t - 1 + 2 - t ⇒ t² - t + 1 = 0
⇒ D = 1 - 4 = -3 < 0
Hence, no real solution is possible in this case.
Case 3: When t ≥ 2, then
t² - t + 2 = t - 1 + 2 - t ⇒ t² - 3t + 5 = 0
⇒ D = 9 - 20 = -11 < 0
Hence, no real solution is possible in this case.
Hence, S is a singleton.

Q.14. If 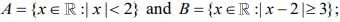 then    (2020)
(1) A ∩ B = (-2, -1)
(2) B - A = 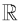- (-2, 5)
(3) A ∪ B = 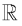- (2, 5)
(4) A - B = (-1, 2)
Ans. (2)
We have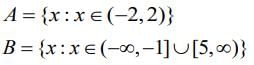

Now, A ∩ B = {x : x ∈ (-2, -1)}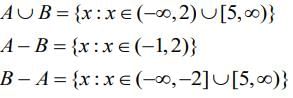


Q.15. Let Z be the set of integers. If A = {x ∈ Z : 2(x + 2)(x² - 5x + 6) = 1} and B = {x ∈ Z : -3 < 2x - 1 < 9}, then the number of subsets of the set A x B, is:    (2019)
(1) 215
(2) 218
(3) 212
(4) 210
Ans. (1)
Let x ∈ A, then
∵
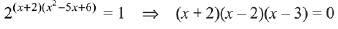
x = -2, 2, 3
A = {-2, 2, 3}
Then, n(A) = 3
Let x ∈ B, then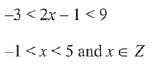

∴ B={0, 1, 2, 3, 4}
n(B) = 5
n(A x B) = 3 x 5 = 15
Hence, Number of subsets of A x B = 2¹⁵

Q.16. Two newspapers A and B are published in a city. It is known that 25% of the city population reads A and 20% reads B while 8% reads both A and B. Further, 30% of those who read A but not B look into advertisements and 40% of those who read B but not A also look into advertisements, while 50% of those who read both A and B look into advertisements. Then the percentage of the population who look into advertisements is:    (2019)
(1) 13.9
(2) 12.8
(3) 13
(4) 13.5
Ans. (1)

% of people who reads A only = 25 - 8 =17%
% of people who read B only = 20 - 8 = 12%
% of people from A only who read advertisement = 17 x 0.3 = 5.1%
% of people from B only who read advertisement = 12 x 0.4 = 4.8%
% of people from A & B both who read advertisement = 8 x 0.5 = 4%
∴ total % of people who read advertisement = 5.1 + 4.8 + 4= 13.9%

Q.17. Let A, B and C be sets such that φ ≠ A ∩ B ⊆ C. Then which of the following statements is not true?    (2019)
(1) B ∩ C ≠ φ)
(2) If (A - B) ⊆ C,then A ⊆ C
(3) (C ∪ A) ∩ (C ∪ B) = C
(4) If (A - C) ⊆ B, then A ⊆ B
Ans. (1)
(1), (2) and (4) are always correct.
In (3) option,
If A = C then A - C = φ
Clearly, φ ⊆ B but A ⊆ B is not always true.

Q.18. 5 students of a class have an average height 150 cm and variance 18 cm . Anew student, whose height is 156 cm, joined them. The variance (in cm ) of the height of these six students is:    (2019)
(1) 16
(2) 22
(3) 20
(4) 18
Ans. (3)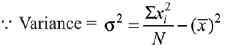


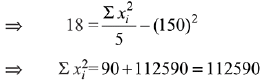
Then, variance of the height of six students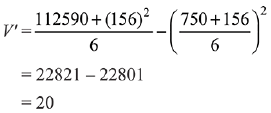


Q.19. A data consists of n observations: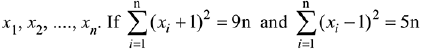

then the standard deviation of this data is:    (2019)
(1) 2
(2) √5
(3) 5
(4) √7
Ans. (2)
Variance is given by,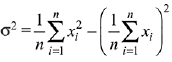

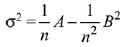   ...(1)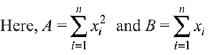

∵
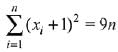
⇒ A + n + 2B = 9n ⇒ A + 2B = 8 ...(ii)
∵
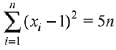
⇒ A + n - 2B - 5n ⇒ A - 2B = An    ...(iii)
From (ii) and (iii),
A = 6n, B = n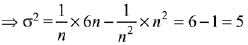



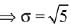
Q.20. The mean of five observations is 5 and their variance is 9.20. If three of the given five observations are 1, 3 and 8, then a ratio of other two observations is:    (2019)
(1) 10 : 3
(2) 4 : 9
(3) 5 : 8
(4) 6 : 7
Ans. (2)
Since mean of x₁, x₂, x₃, x₄ and x₅ is 5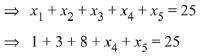

⇒ x₄ + x₅ = 13    (1)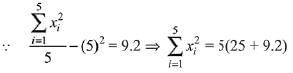

= 125 + 46 = 171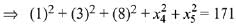

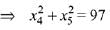    (2)

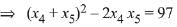
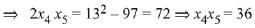    (3)


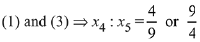
Q.21. If mean and standard deviation of 5 observations x₁, x₂, x₃, x₄, x₅ are 10 and 3, respectively, then the variance of 6 observations x₁, x₂,.... x₅ and - 50 is equal to:
(1) 509.5
(2) 586.5
(3) 582.5
(4) 507.5
Ans. (4)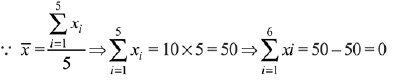



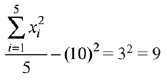
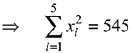
Then,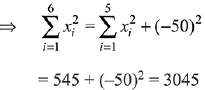



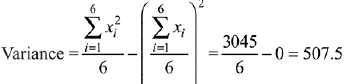
Q.22. The outcome of each of 30 items was observed; 10 items gave an outcome 1/2 - d each, 10 items gave outcome 1/2 each and the remaining 10 items gave outcome 1/2 + d each. If the variance of this outcome data is 4/3 then |d| equals:    (2019)
(1) 2/3
(2) 2
(3) √5/2
(4) √2
Ans. (4)
Outcomes are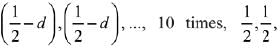  

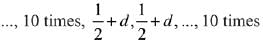
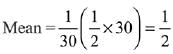
Variance of the outcomes is,



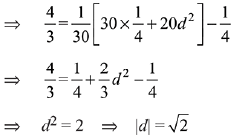
Q.23. A bag contains 30 white balls and 10 red balls. 16 balls are drawn one by one randomly from the bag with replacement. If X be the number of white balls drawn, then  is equal to:    (2019)
(1) 4
(2) 4√3
(3) 3√2
(4) 4√3 / 3
Ans. (2)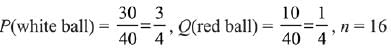




Q.24. If the sum of the deviations of 50 observations from 30 is 50, then the mean of these observations is:    (2019)
(1) 30
(2) 51
(3) 50
(4) 31
Ans. (4)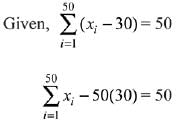

⇒

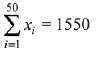
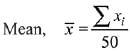
= 1550/50
= 31

Q.25. There are m men and two women participating in a chess tournament. Each participant plays two games with every other participant. If the number of games played by the men between themselves exceeds the number of games played between the men and the women by 84, then the value of m is    (2019)
(1) 12
(2) 11
(2) 9
(4) 7
Ans. (1)



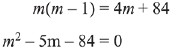
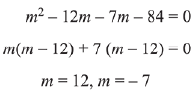
∴ m > 0
m = 12

Q.26. The mean and the variance of five observations arc 4 and 5.20, respectively. If three of the observations are 3,4 and 4; then the absolute value of the difference of the other two observations, is:    (2019)
(1) 7
(2) 5
(3) 1
(4) 3
Ans. (1)
Let two observations be x₁ and x₂, then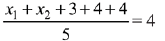

⇒ x₁ + x₂ = 9 ...(1)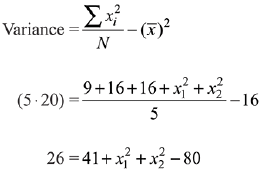

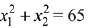 ...(2)
From (1) and (2);
x₁ = 8, x₂ = 1
Hence, the required value of the difference of other two observations = |x₁ - x₂| = 7

Q.27. The mean and variance of seven observations are 8 and 16, respectively. If 5 of the observations are 2, 4, 10, 12, 14, then the product of the remaining two observations is:    (2019)
(1) 45
(2) 49
(3) 48
(4) 40
Ans. (3)
Let the remaining numbers are a and b.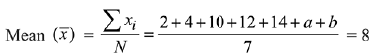

⇒ a + b = 14   (1)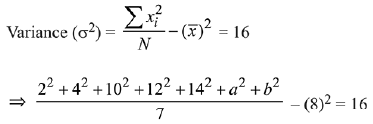

⇒ a² + b² = 100   (2)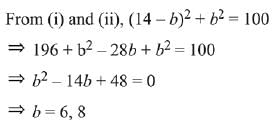


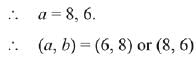
Hence, the product of the remaining two observations = ab = 48

Q.28. A student scores the following marks in five tests: 45, 54, 41, 57, 43. His score is not known for the sixth test. If the mean score is 48 in the six tests, then the standard deviation of the marks in six tests is:    (2019)
(1) 10/√3
(2) 100/3
(3) 10/3
(4) 100/√3
Ans. (1)
∵ Mean score = 48
Let unknown score be x,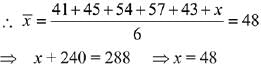

Now,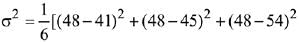  



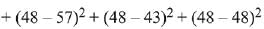
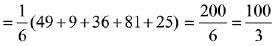
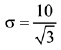
Q.29. If the standard deviation of the numbers -1, 0, 1, k is √5 where k > 0, then k is equal to:    (2019)
(1) 2√6
(2)
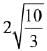
(3)
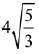
(4) √6
Ans. (1)
Mean of given observation = k/4
∵ Standard deviation = 5
∴ σ² = 5    ...(1)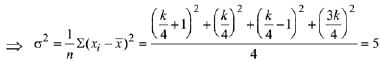
 ...(2)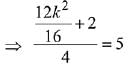

⇒ k = 2√6

Q.30. The mean and the median of the following ten numbers in increasing order 10, 22, 26, 29, 34, x, 42, 67, 70, y are 42 and 35 respectively, then y/x is equal to:    (2019)
(1) 9/4
(2) 7/2
(3) 8/3
(4) 7/3
Ans. (4)
Ten numbers in increasing order are 10, 22, 26,29, 34, x, 42, 67, 70, y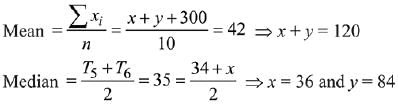



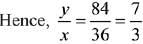
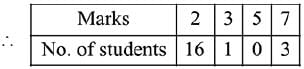
Q.31. If for some x ∈ R, the frequency distribution of the marks obtained by 20 students in a test is:

then the mean of the marks is:    (2019)
(1) 3.2
(2) 3.0
(3) 2.5
(4) 2.8
Ans. (4)
Number of students are,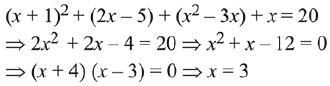




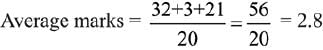
Q.32. If both the mean and the standard deviation of 50 observations x₁, x₂,....., x₅₀ are equal to 16, then the mean of -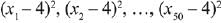 is:    (2019)
(1) 400
(2) 380
(3) 525
(4) 480
Ans. (1)
Given, mean and standard deviation are equal to 16.

and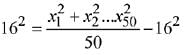


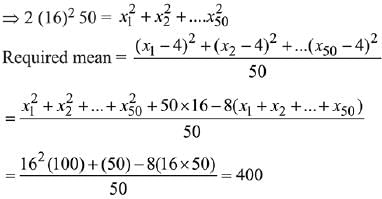
Q.33. If the data x₁, x₂, ..... , x₁₀ is such that the mean of first four of these is 11, the mean of the remaining six is 16 and the sum of squares of all of these is 2,000 ; then the standard deviation of this data is:    (2019)
(1) 2√2    
(2) 2    
(3) 4    
(4) √2
Ans. (2)
According to the question,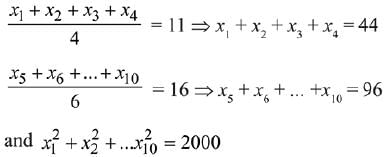

∵ standard deviation,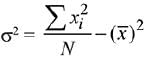
 

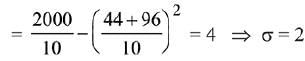
Q.34. If the Boolean expression 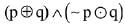 is equivalent to p ∧ q , where 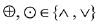then the ordered pair  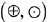is:    (2019)
(1) (∨,∧)    
(2) (∨, ∨)
(3) (∧, ∨) 
(4) (∧, ∧)
Ans. (3)
Check each option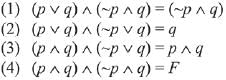


Q.35. The logical statement [~ (~ P ∨ q) ∨ (p ∧ r)] ∧ (~ p ∧ r)is equivalent to:    (2019)
(1) (~ p ∧ ~ q) ∧ r
(2) ~ p ∨ r
(3) (p ∧ r) ∧ ~ q    
(4) (p ∧ ~ q) ∨ r
Ans. (3)
Logical statement,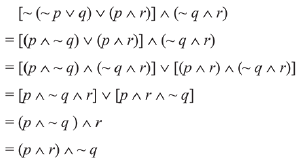


Q.36. Consider the statement: “P(n) : n² - n + 41 is prime." Then which one of the following is true?    (2019)
(1) Both P(3) and P(5) are true.
(2) P(3) is false but P(5) is true.
(3) Both P(3) and P(5) are false.
(4) P(5) is false but P(3) is true.
Ans. (1)
P(n) = n² - n + 41
⇒ P(3) = 9 - 3 + 41 = 47 (prime)
& P(5) = 25 - 5 + 41 = 61 (prime)
∴ P(c) and P(5) are both prime i.e., true.

Q.37. Consider the following three statements:
P : 5 is a prime number.
Q : 7 is a factor of 192.
R : L.C.M. of 5 and 7 is 35.
Then the truth value of which one of the following statements is true?    (2019)
(1) (~ P) ∨ (Q ∧ R)
(2) (P ∧ Q) ∨ (~R)
(3) (~P) ∧ (~Q ∧ R)
(4) P ∧ (~ Q ∧ R)
Ans. (4)
P is True, Q is False and R is True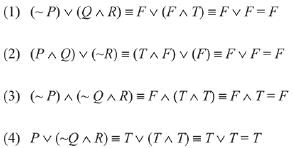


Q.38. If q is false and p ∧ q ↔ r is true, then which one of the following statements is a tautology?    (2019)
(1) (p ∨ r) → (p ∧ r)
(2) (p ∧ r) → (p ∨ r)
(3) p ∧ r
(4) p∨ r
Ans. (2)
q is false and [(p ∧ q) ↔ r] is true
As (p ∧ q) is false
[False ↔ r] is true
Hence r is false
Option (1): says p ∨ r,
Since r is false
Hence (p ∨ r) can either be true or false
Option (2): says (p ∧ r) → (p ∨ r)
(p ∧ r) is false
Since, F → T is true and
F → F is also true
Hence, it is a tautology
Option (3): (p ∨ r) → (p ∧ r)
i.e. (p ∨ r) → F
It can either be true or false
Option (4): (p ∧ r),
Since, r is false
Hence, (p ∧ r) is false.

Q.39. Contrapositive of the statement “If two numbers are not equal, then their squares are not equal”, is:    (2019)
(1) If the squares of two numbers are not equal, then the numbers are equal.
(2) If the squares of two numbers are equal, then the numbers are not equal.
(3) If the squares of two numbers are equal, then the numbers are equal.
(4) If the squares of two numbers are not equal, then the numbers are not equal.
Ans. (3)
Contrapositive of “If A then B” is “If -B then -A". Hence contrapositive of “If two numbers are not equal, then their squares are not equal” is “If squares of two numbers are equal, then the two numbers are equal”.

Q.40. The Boolean expression ((p ∧ q) ∨ (p∨ - q)) ∧ (~ p∧ ~ q) is equivalent to:    (2019)
(1) p ∧ q 
(2) p∧ (~ q)
(3) (~ p) ∧ (~ q)
(4) p ∨ (~ q)
Ans. (3)
Consider the Boolean expression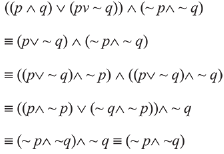


Q.41. The expression - (- p → q) is logically equivalent to:    (2019)
(1) - p ∧ - q    
(2) p ∧ - q
(3) - P ∧ q    
(4) p ∧ q
Ans. (1)


Q.42. The contrapositive of the statement "If you are born in India, then you are a citizen of India", is:    (2019)
(1) If you are not a citizen of India, then you are not born in India.
(2) If you are a citizen of India, then you are born in India.
(3) If you are born in India, then you are not a citizen of India.
(4) If you are not born in India, then you are not a citizen of India.
Ans. (1)
S: "If you are bom in India, then you are a citizen of India."
Contrapositive of p → q is ~ q → ~ p
So contrapositive of statement S will be:
"If you are not a citizen of India, then you are not bom in India."

Q.43. If a point R(4, y, z) lies on the line segment joining the points P(2, -3, 4) and Q(8, 0, 10), then distance of R from the origin is:    (2019)
(1) 2√14
(2) 2√21
(3) 6
(4) √53
Ans. (1)
Here, P, Q, R are collinear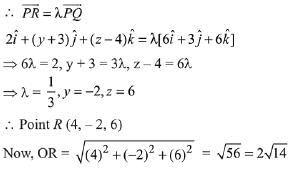


Q.44. For any two statements p and q, the negation of the expression p ∨ (~ p ∧ q) is:    (2019)
(1) ~ p ∧ ~ q
(2) p ∧ q
(3) p ↔ q
(4) ~ p ∨ ~ q
Ans. (1)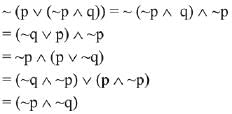


Q.45. If p ⇒ (q ∨ r) is false, then the truth values of p, q, r are respectively:    (2019)
(1) F, T, T
(2) T, F, F
(3) T, T, F
(4) F, F, F
Ans. (2)
For p ⇒ q ∨ r to be F.
r should be F and p ⇒ q should be F
for p ⇒ q to be F, p ⇒ T and q ⇒ F
p, q, r ≡ T, F, F

Q.46. Which one of the following Boolean expressions is a tautology?    (2019)
(1) (p ∧ q) ∨ (p ∧ - q)
(2) (p ∨ q) ∨ (p ∨ ∼ q)
(3) (p ∨ q) ∧ (p ∨ ~ q)
(4) (p ∨ q) ∧ (~p ∨ ∼ q)
Ans. (2)
(p ∨ q) ∨ (p ∨ ~q) = p ∨ (q ∨ p) ∨ ~ q
= (p ∨ p) ∨ (q ∨ ~ q) = p ∨ T = T
Hence first statement is tautology.

Q.47. The negation of the Boolean expression ~ s ∨ (~ r ∧ s) is equivalent to:    (2019)
(1) ~s ∧~r
(2) r 
(3) s ∨ r
(4) s ∧ r
Ans. (4)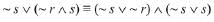

≡ (~ s ∨ ~ r)    (∵ ∼ s ∨ s) is tautology)
≡ ~(s ∧ r)
Hence, its negation is s ∧ r.

Q.48. If the truth value of the statement p → (~q ∨ r) is false (F), then the truth values of the statements p, q, r are respectively.    (2019)
(1) T, T, F
(2) T, F, F
(3) T, F, T
(4) F, T, T
Ans. (1)
Given statement p → (~ q ∨ r) is False.
⇒ p is True and ~ q ∨ r is False
⇒ p is True and ~ q is False and r is False
∴ truth values of p, q r are T, T, F respectively.

Q.49. The Boolean expression - (p ⇒ (~ q)) is equivalent to:    (2019)
(1) p ∧ q
(2) q ⇒ ~ p
(3) p ∨ q
(4) (~ p) ⇒ q
Ans. (1)
Given Boolean expression is,
~ (p ⇒ (~ q))  {∵ p ⇒ q is same as ~p ∨ q}
≡ ∼((∼ p) ∨ (~ q)) = p ∧ q

Q.50. The Boolean expression ~(p ν q) ν (~p ∧ q) is equivalent to:    (2018)
(1) ~p
(2) p
(3) q
(4) ~q
Ans. (1)


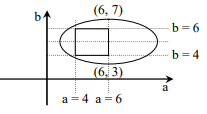
Q.51. Two sets A and B are as under:
A={(a, b) ∈ R x R : |a - 5| <1 and |b - 5|<1};
B={(a, b) ∈ R x R : 4(a - 6)² + 9(b - 5)² ≤ 36 }. Then:    (2018)
(1) B ⊂ A  
(2) A⊂B
(3) A ∩ B = Φ (an empty set)
(4) neither A ⊂ B nor B ⊂ A
Ans. (3)



Q.52. If 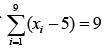 and 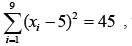 then the standard deviation of the 9 items x₁ x₂, …., x₉ is:    (2018)
(1) 9
(2) 4
(3) 2
(4) 3
Ans. (3)
x_i - 5 = y_i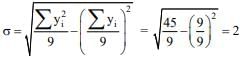 


Q.53. Consider the following two binary relations on the set A = {a, b, c}: R₁ = {(c, a), (b, b), (a, c), (c, c), (b, c), (a, a)} and R₂ = {(a, b), (b, a), (c, c), (c, a), (a, a), (b, b), (a, c)}.Then:    (2018)
(1) both R₁ and R₂ are transitive 
(2) both R₁ and R₂ are not symmetric 
(3) R₁ is not symmetric but it is transitive 
(4) R₂ is symmetric but it is not transitive 
Ans. (4)
R₁ ∈ (b, c) but R₁ ∉ (c, b)
Example R₁ is not symmetric  
in R₁; (b, c) ∈ R₁ and (c, a) ∈ R₁ but (b, a) ∉ R₁ 
So R₁ is not transitive
R₂ is symmetric
is R₂ ; (b, a) ∈ R₂ and (a, c) ∈ R₂ but (b, c) ∉ R₂
So R₂ is not transitive

Q.54. The mean and the standard deviation (s.d.) of five observations are 9 and 0, respectively. If one of the observations is changed such that the mean of the new set of five observations becomes 10, then their s.d. is:    (2018)
(1) 2
(2) 4
(3) 0
(4) 1
Ans. (1)
Here mean =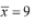

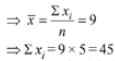
Now, standard deviation = 0
∴ all the five terms are same i.e., 9.
Now for changed observation

= 2

Q.55. Let N denote the set of all natural numbers. Define two binary relations on N as R₁ = {(x, y) ∈ N × N : 2x + y = 10} and R₂ = {(x, y) Î N × N : x + 2y = 10}. Then    (2018)
(1) Both R₁ and R₂ are transitive relations
(2) Range of R₂ is {1, 2, 3, 4}
(3) Range of R₁ is {2, 4, 8}
(4) Both R₁ and R₂ are symmetric relations
Ans. (2)
 

Q.56. The function 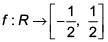 defined as 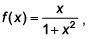is    (2017)
(1) Neither injective nor surjective
(2) Invertible
(3) Injective but not surjective
(4) Surjective but not injective
Ans. (4)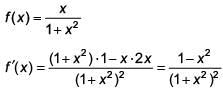

f '(x) changes sign in different intervals.
∴ Not injective.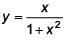

yx² - x+ y = 0
For y ≠ 0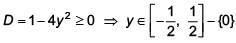 

For, y = 0  ⇒ x = 0
∴ Part of range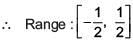 

∴ Surjective but not injective. 

Q.57. The following statement (p → q) → [(~ p → q) → q] is    (2017) 
(1) A fallacy
(2) A tautology
(3) Equivalent to ~ p → q
(4) Equivalent to  p → ~ q
Ans. (2)


Q.58. The mean age of 25 teaches in a school is 40 years. A teacher retires at the age of 60 years and a new teacher is appointed in his place. If now the mean age of the teachers in this school is 39 years, then the age ( in years ) of the newly appointed teachers is:    (2017)
(1) 35
(2) 40
(3) 25
(4) 30
Ans. (1)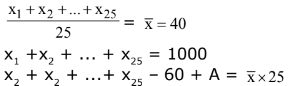

1000 - 60 + A = 39 × 25 = 975
A = 975 - 940 = 35

Q.59. The proposition (~ p) V (P ^ ~ q) is equalvalent to:    (2017)
(1) P → ~q
(2) P ^ ~ q
(3) q → p
(4) p v ~ q
Ans. (2)
(~ p) V ( P ^ ~ q)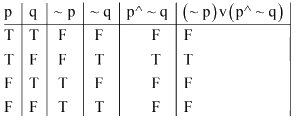


Q.60. The sum of 100 observations and the sum of their squares are 400 and 2475, respectively. Later on, three observations, 3, 4 and 5, were found to be incorrect. If the incorrect observations are omitted, then the variance of the remaining observations is:    (2017)
(1) 8.25
(2) 8.50
(3) 9.00
(4) 8.00
Ans. (3)



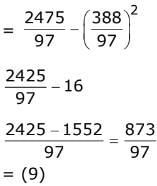
Q.61. Contrapositive of the statement
'If two numbers are not equal, then their squares are not equal', is:    (2017)
(1) If the squares of two numbers are equal, then the numbers are not equal
(2) If the squares of two numbers are not equal, then the numbers are equal
(3) If the squares of two numbers are not equal, then the numbers are not equal
(4) If the squares of two numbers are equal, then the numbers are equal.
Ans. (4)
p → q
contrapositive is
~ q → ~ p

Q.62. If the standard deviation of the numbers 2, 3, a and 11 is 3.5, then which of the following is true?    (2016)
(1) 3a² - 26a + 55 = 0
(2) 3a² - 32a + 84 = 0
(3) 3a² - 34a + 91 = 0
(4) 3a² - 23a + 44 = 0
Ans. (2)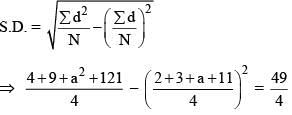

⇒ (4a² + 536) - (a² + 32a + 256) = 196 => 3a² - 32a + 84 = 0

Q.63. The Boolean Expression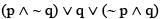is equivalent to:    (2016)
(1) ~ p ∧ q
(2) p ∧ q
(3) p ν q
(4) p ν ~ q
Ans. (3)
(p ∧ ~ q) ν q ν (~ p ∧ q)


Q.64. If the mean deviation of the numbers 1, 1 + d, ..., 1 + 100 d from their mean is 255, then a value of d is:    (2016)
(1) 10
(2) 20.2
(3) 5.05
(4) 10.1
Ans. (4)
Mean is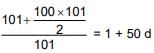
sum of deviation about mean is
50 d + 49d + ................... d + 0 + d + ........ + 50 d
= 50.51 d
Mean deviation =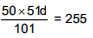


Q.65. Consider the following two statements:
P: If 7 is an odd number, then 7 is divisible by 2.
Q: If 7 is a prime number, then 7 is an odd number.
If V₁ is the truth value of contrapositive of P and V₂ is the truth value of contrapositive of Q, then the ordered pair (V₁, V₂) equals:    (2016)
(1) (F, T)
(2) (T, F)
(3) (F, F)
(4) (T, T)
Ans. (1)
Statement P is False
Statement Q is True.
V₁ ≡ F
V₂ ≡ T
1

Q.66. The contrapositive of the following statement,
" If the side of a square doubles, then its area increases four times", is    (2016)
(1) If the area of a square does not increase four times, then its side is not doubled.
(2) If the area of a square increases four times, then its side is not doubled.
(3) If the area of a square increases four times, then its side is doubled.
(4) If the side of a square is not doubled, then its area does not increase four times.
Ans. (1)
p ≡ The side of a square doubles
q ≡ Area of square increases four time
so the contrapositive of p → q is ~ q → ~ P

Q.67. The mean of 5 observations is 5 and their variance is 124. If three of the observations are 1, 2 and 6, then the mean deviation from the mean of the data is    (2016)
(1) 2.5
(2) 2.8
(3) 2.6
(4) 2.4
Ans. (2)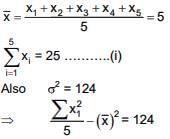


Now,