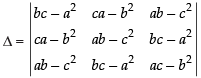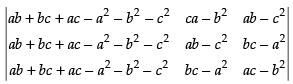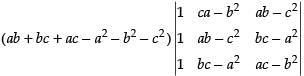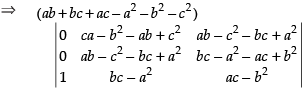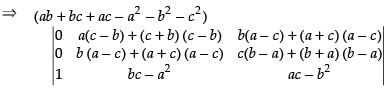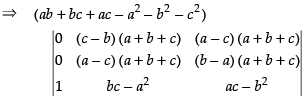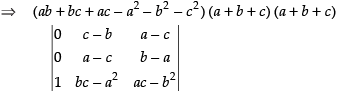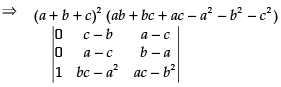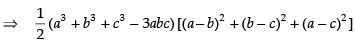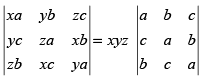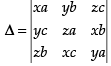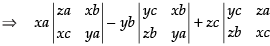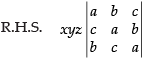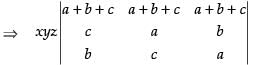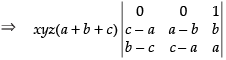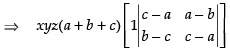Using the properties of determinants in Exercises 1 to 6, evaluate:
Q.1. 
Ans.
Let
C1 → C1 - C2

= (x + 1) (x2 – 2x + 2) – 0
= x3 – 2x2 + 2x + x2 – 2x + 2 = x3 – x2 + 2
Q.2. 
Ans.
Let
C1 → C1 + C2 + C3

(Taking a + x + y + z common)
R1 → R1 - R2, R2 → R2 - R3

Expanding along C1 = (a + x+y +z)  = a2(a + x + y + z)
= a2(a + x + y + z)
Q.3. 
Ans.
Let
Taking x2, y2 and z2 common from C1, C2 and C3 respectively

Expanding along R1

= x2y2z2 [- x(0 - yz) + x( yz - 0)]
= x2y2z2(xyz + xyz) = x2y2z2(2xyz) = 2x3y3z3
Q.4. 
Ans.
Let
C1 → C1 + C2 + C3

Taking (x + y + z) common from C1

R1 → R1 - R2, R2 → R2 - R3

Expanding along C1

= (x+y+ z) [(-x - 2y)(-y - 2z) -(2y +z)(-x +y)]
= (x + y + z) (xy + 2zx + 2y2 + 4yz + 2xy – 2y2 + zx – zy)
= (x + y + z) (3xy + 3zx + 3yz) = 3(x + y + z) (xy + yz + zx)
Q.5. 
Ans.
Let
C1 → C1 + C2 + C3

Taking (3x + 4) common from C1

R1 → R1 - R2, R2 → R2 - R3

Expanding along C1

Q.6. 
Ans.
Let
R1 → R1 + R2 + R3

Taking (a + b + c) common from R1

C1 → C1 - C2, C2 → C2 - C3

Taking (b + c + a) from C1 and C2

Expanding along R1

Using the properties of determinants in Exercises 7 to 9, prove that:
Q.7. 
Ans.
L.H.S. =
R1 → xR1, R2 → yR2, R3 → zR3 and dividing the determinant by xyz.

Taking xyz common from C1 and C2

C3 → C3 + C1

Taking (xy + yz + zx) common from C3

[∵ C2 and C3 are identical]
L.H.S. = R.H.S. Hence proved.
Q.8. 
Ans.
L.H.S. =
C1 → C1 - (C2 + C3)

Taking –2 common from C1

R2 → R2 - R3

Expanding along C1
= - 2 [ x - zy- zy ] = – 2(– 2xyz) = 4xyz R.H.S.
L.H.S. = R.H.S.
Hence, proved.
Q.9. 
Ans.
L.H.S.=
R1 → R1 - R2, R2 → R2 - R3

Taking (a – 1) common from C1 and C2

Expanding along C3

= (a – 1)2 (a + 1 – 2) = (a – 1)2 (a – 1) = (a – 1)3 R.H.S.
L.H.S.= R.H.S.
Hence, proved.
Q.10. If A + B + C = 0, then prove that
Ans.
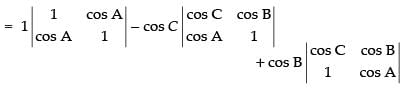
L.H.S. = 
Expanding along C1

= 1(1 – cos2 A) – cos C(cos C – cos A cos B) + cos B (cos A cos C – cos B)
= sin2 A – cos2 C + cos A cos B cos C + cos A cos B cos C – cos2 B
= sin2 A – cos2 B – cos2 C + 2 cos A cos B cos C
= – cos (A + B) × cos (A - B) - cos2 C + 2 cos A cos B cos C
[∵ sin2 A - cos2 B= - cos (A +B)× cos (A - B)]
= - cos ( - C) × cos (A - B) + cos C (2 cos A cos B - cos C) [∵ A + B + C = 0]
= – cos C(cos A cos B + sin A sin B) + cos C(2 cos A cos B – cos C)
= – cos C(cos A cos B + sin A sin B – 2 cos A cos B + cos C)
= – cos C(– cos A cos B + sin A sin B + cos C)
= cos C(cos A cos B – sin A sin B – cos C)
= cos C[cos(A + B) – cos C ]
= cos C[cos (– C) – cos C] [∵ A + B = - C]
= cos C[cos C - cos C] = cos C × 0 = 0 R.H.S.
L.H.S. = R.H.S.
Hence, proved.
Q.11. If the co-ordinates of the vertices of an equilateral triangle with sides of length ‘a’ are (x1, y1), (x2, y2), (x3, y3), then
Ans.
Area of triangle whose vertices are (x1, y1), (x2, y2) and (x3, y3)

Let ⇒
⇒
But area of equilateral triangle whose side is ‘a‘ =


Hence, proved.
Q.12. Find the value of θ satisfying
Ans.
Let

C1 → C1 - C2
⇒
Taking 7 common from C1
⇒
⇒
Expanding along C1
⇒
⇒ –2 + 7 sin 3θ + 2 (cos 2θ – 3 sin 3θ) = 0
⇒ – 2 + 7 sin 3θ + 2 cos 2θ – 6 sin 3θ = 0
⇒ – 2 + 2 cos 2θ + sin 3θ = 0
⇒ – 2 + 2 (1 – 2 sin2 θ) + 3 sin θ – 4 sin3 θ = 0
⇒ – 2 + 2 – 4 sin2 θ + 3 sin θ – 4 sin3 θ = 0
⇒ – 4 sin3 θ – 4 sin2 θ + 3 sin θ = 0
⇒ – sin θ(4 sin2 θ + 4 sin θ – 3) = 0
sin θ = 0 or 4 sin2 θ + 4 sin θ – 3 = 0
∴ θ = nπ or 4 sin2 θ + 6 sin θ – 2 sin θ – 3 = 0 when n ∈ I
⇒ 2 sin θ(2 sin θ + 3) - 1 (2 sin θ + 3) = 0
⇒ (2 sin θ + 3)(2 sin θ – 1) = 0
⇒ 2 sin θ + 3 = 0 or 2 sin θ - 1 = 0

 is not possible as – 1 ≤ x ≤ 1
is not possible as – 1 ≤ x ≤ 1

Hence,
Q.13. If , then find values of x.
, then find values of x.
Ans.
Let 

R1 → R1 + R2 + R3
⇒
Taking (12 + x) common from R1,
⇒
C1 → C1 - C2, C2 → C2 - C3

Expanding along R1
⇒
(12 + x) (4x2 – 0) = 0 ⇒ 12 + x = 0 or 4x2 = 0
⇒ x = -12 or x = 0
Q.14. If a1, a2, a3, …, ar are in G.P., then prove that the determinant
 is independent of r.
is independent of r.
Ans.
If a1, a2, a3, … ar be the terms of G.P., then
an = ARn–1
(where A is the first term and R is the common ratio of the G.P. )
∴ar+1 = ARr+1–1 = ARr; ar+5 = ARr+5–1 = ARr+4
ar+9 = ARr +9-1 = ARr +8 ; ar+7 = ARr+7–1 = ARr+6
ar+11 = ARr+11–1 = ARr+10; ar+15 = ARr+15–1 = ARr+14
ar+17 = AR r +17-1 = ARr +16 ; ar+21 = ARr+21–1 = ARr+20
∴ The determinant becomes

Taking ARr, ARr+6 and ARr+10 common from R1, R2 and R3 respectively.


[∵ R1 and R2 are identical rows]
= 0
Hence, the given determinant is independent of r.
Q.15. Show that the points (a + 5, a – 4), (a – 2, a + 3) and (a, a) do not lie on a straight line for any value of a.
Ans.
If the given points lie on a straight line, then the area of the triangle formed by joining the points pairwise is zero.

R1 → R1 - R2, R2 → R2 - R3
⇒
Expanding along C3

As 7 ≠ 0. Hence,, the three points do not lie on a straight line for any value of a.
Q.16. Show that the ∆ABC is an isosceles triangle if the determinant

Ans.

C1 → C1 - C2, C2 → C2 - C3

Taking (cos A – cos B) and (cos B – cos C) common from C1 and C2 respectively.


⇒ (cos A - cos B) (cos B- cos C) [cos B + cos C + 1 - cos A - cos B - 1] = 0
⇒ (cos A – cos B) (cos B – cos C) (cos C – cos A) = 0
cos A – cos B = 0 or cos B – cos C = 0
or cos C – cos A = 0
⇒ cos A = cos B or cos B = cos C or cos C = cos A
⇒ ∠A = ∠C or ∠B = ∠C ⇒ ∠A = ∠B
Hence, ΔABC is an isosceles triangle.
Q.17. Find A–1 if and show that
and show that
Ans.
Here,

= 0 – 1 (0 – 1) + 1 (1 – 0)
= 1 + 1 = 2 ≠ 0 (non-singular matrix.)
Now, co-factors,



∴
Now, A2 =

Hence, A2 = 
Now, we have to prove that

Hence, proved.
Long Answer (L.A.)
Q.18. If find A–1. Using A–1, solve the system of linear equations x – 2y = 10 , 2x – y – z = 8 , –2y + z = 7.
find A–1. Using A–1, solve the system of linear equations x – 2y = 10 , 2x – y – z = 8 , –2y + z = 7.
Ans.
Given that

= 1(–1 – 2) – 2(–2 – 0) + 0
= – 3 + 4 = 1 ≠ 0 (non-singular matrix.)
Now co-factors,


∴
⇒
Now, the system of linear equations is given by x – 2y = 10, 2x – y – z = 8 and – 2y + z = 7, which is in the form of CX = D.

where
∵ (AT)–1 = (A–1)T

Hence, x = 0, y = – 5 and z = – 3
Q.19. Using matrix method, solve the system of equation
3x + 2y – 2z = 3, x + 2y + 3z = 6, 2x – y + z = 2.
Ans.
Given that
3x + 2y – 2z = 3
x + 2y + 3z = 6
2x – y + z = 2
Let

= 3(2 + 3) – 2(1 – 6) – 2(– 1 – 4)
= 15 + 10 + 10 = 35 ≠ 0 non-singular matrix
Now, co-factors,





Hence, x = 1, y = 1 and z = 1.
Q.20. Given find BA an⇒d use this to solve the system of equations y + 2z = 7, x – y = 3, 2x + 3y + 4z = 17.
find BA an⇒d use this to solve the system of equations y + 2z = 7, x – y = 3, 2x + 3y + 4z = 17.
Ans.
We have,
BA =

∴
The given equations can be re-write as,
x – y = 3, 2x + 3y + 4z = 17 and y + 2z = 7
∴
⇒

Hence, x = 2, y = – 1 and z = 4
Q.21. If a + b + c ≠ 0 and then prove that a = b = c.
then prove that a = b = c.
Ans.
Given that: a + b + c ≠ 0 and
C1 → C1 + C2 + C3
⇒
⇒ (Taking a + b + c common from C1)
(Taking a + b + c common from C1)
⇒
R1 → R1 - R2 and R2 → R2 - R3
⇒
Expanding along C1
⇒
⇒ (b – c) (a – b) – (c – a)2 = 0
⇒ ab – b2 – ac + bc – c2 – a2 + 2ac = 0
⇒ – a2 – b2 – c2 + ab + bc + ac = 0
⇒ a2 + b2 + c2 – ab – bc – ac = 0
⇒ 2a2 + 2b2 + 2c2 – 2ab – 2bc – 2ac = 0
(Multiplying both sides by 2)
⇒ (a2 + b2 – 2ab) + (b2 + c2 – 2bc) + (a2 + c2 – 2ac) = 0
⇒ (a – b)2 + (b – c)2 + (a – c)2 = 0
It is only possible when (a – b)2 = (b – c)2 = (a – c)2 = 0
∴ a = b = c Hence, proved.
Q.22. Prove that is divisible by a + b + c and find the quotient.
is divisible by a + b + c and find the quotient.
Ans.
Let
C1 → C1 + C2 + C3
⇒
Taking ab + bc + ac – a2 – b2 – c2 common from C1

R1 → R1 - R2 and R2 → R2 - R3





Expanding along C1
⇒ (a +b + c)2 (ab + bc + ac - a2 - b2 - c2 )
⇒ (a + b + c)2(ab + bc + ac - a2 - b2 - c2)[(c - b) (b - a)-(a- c)2]
⇒ (a + b + c)2 (ab + bc + ac - a2- b2- c2 )(bc - ca - b2+ ab - a2- c2 + 2ac)
⇒ (a + b + c)2 (ab + bc + ac - a2- b2- c2 )(ab + bc + ca - a2- b2- c2 )
⇒ (a + b + c)2 (ab + bc + ac - a2 - b2 - c2)2
⇒ (a + b + c) (a + b + c) (a2 + b2 + c2 - ab - bc - ac)2
Hence, the given determinant is divisible by a + b + c and the quotient is
(a + b + c) (a2 + b2 + c2 - ab - bc - ac)2
⇒ (a + b + c) (a2 + b2 + c2 - ab - bc - ac) (a2 + b2 + c2 - ab - bc - ac)
⇒ (a3 + b3 + c3 - 3abc) (a2 + b2 + c2 - ab - bc - ac)
⇒ (a3 + b3 + c3- 3abc) (2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ac)

Q.23. If x + y + z = 0, prove that
Ans.
L.H.S.
Let 
Expanding along R1

⇒ xa(yza2 – x2bc) – yb(y2ac – xzb2) + zc(xyc2 – z2ab)
⇒ xyza3 – x3abc – y3abc + xyzb3 + xyzc3 – z3abc
⇒ xyz(a3 + b3 + c3) – abc(x3 + y3 + z3)
⇒ xyz(a3 + b3 + c3) – abc(3xyz)
[(∵ x + y + z = 0) (∴ x3 + y3 + z3 = 3xyz)]
⇒ xyz(a3 + b3 + c3 – 3abc)

R1 → R1 + R2 + R3


(Taking a + b + c common from R1)
C1 → C1 - C2, C2 → C2 - C3

Expanding along R1

⇒ xyz(a + b+ c) [(c - a)2 - (b- c) (a - b)]
⇒ xyz(a + b + c)(c 2 + a2- 2ca - ab + b2+ ac - bc)
⇒ xyz(a + b+ c)( a2 + b2 + c2 - ab - bc - ca)
⇒ xyz(a3 + b3 + c3 - 3abc)
[a3 + b3 + c3 - 3abc = (a + b + c) (a2 + b2 + c2 - ab - bc - ca)]
L.H.S. = R.H.S.
Hence, proved.
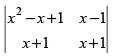
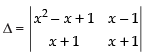
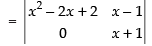
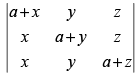
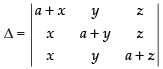
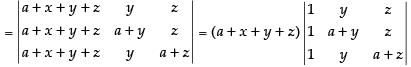
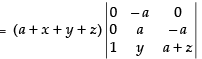
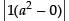 = a2(a + x + y + z)
= a2(a + x + y + z)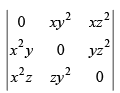
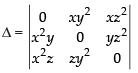
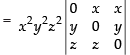
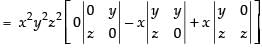
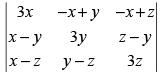
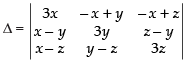
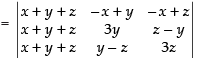
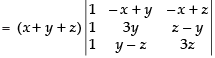
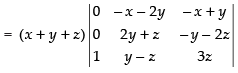
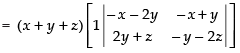
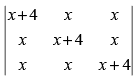
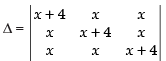
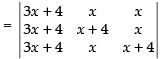
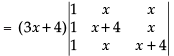
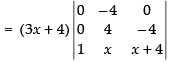
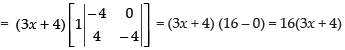
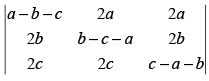
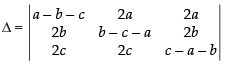
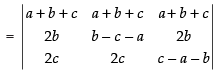
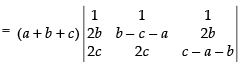
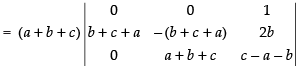
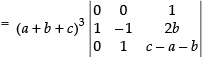
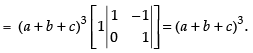
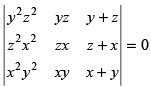
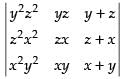
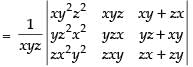
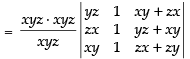
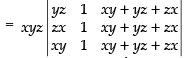
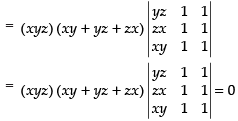
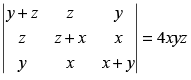
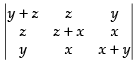
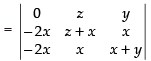

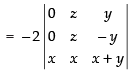
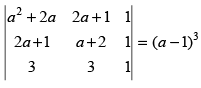
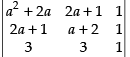
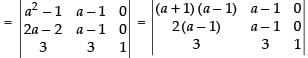
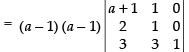
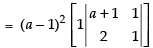
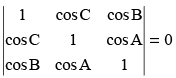
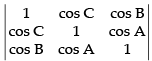
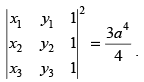
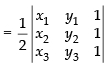
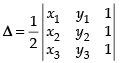 ⇒
⇒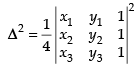
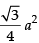
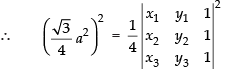
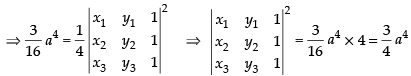
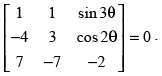
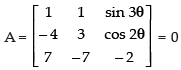
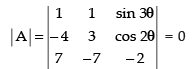
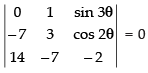
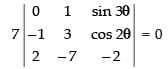
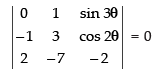
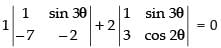
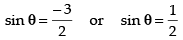
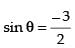 is not possible as – 1 ≤ x ≤ 1
is not possible as – 1 ≤ x ≤ 1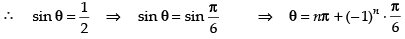
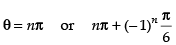
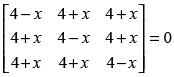 , then find values of x.
, then find values of x.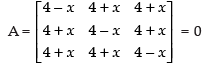
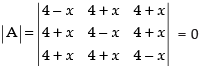
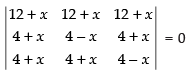
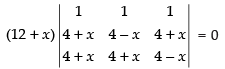
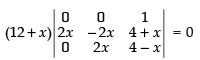
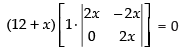
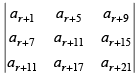 is independent of r.
is independent of r.
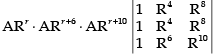
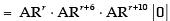
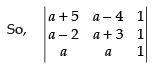
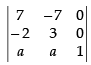

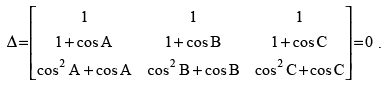
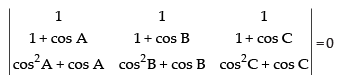
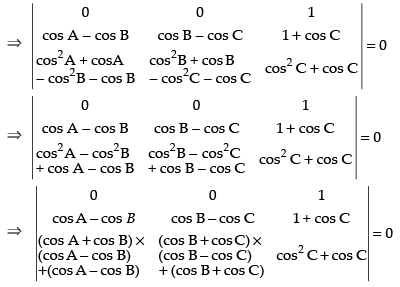
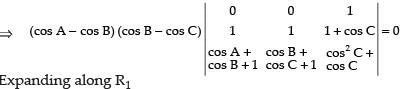
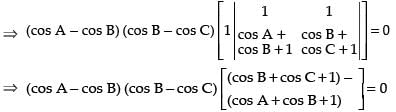
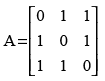 and show that
and show that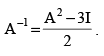
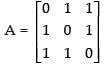
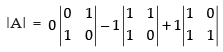
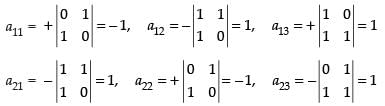
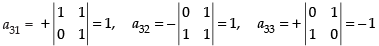

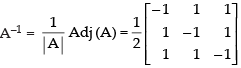
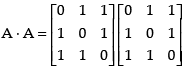

 find A–1. Using A–1, solve the system of linear equations x – 2y = 10 , 2x – y – z = 8 , –2y + z = 7.
find A–1. Using A–1, solve the system of linear equations x – 2y = 10 , 2x – y – z = 8 , –2y + z = 7.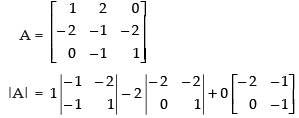
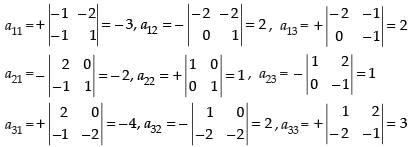
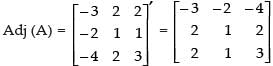

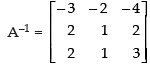
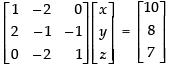
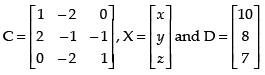
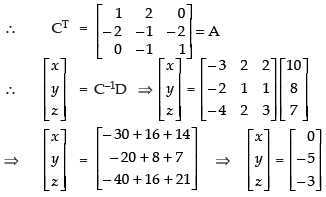
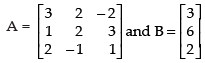
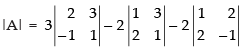
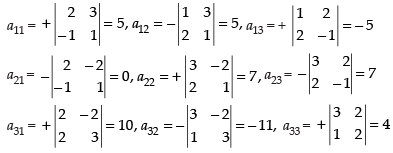
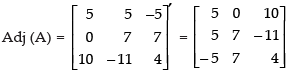
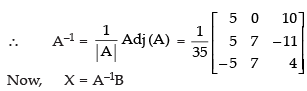

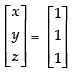
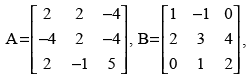 find BA an⇒d use this to solve the system of equations y + 2z = 7, x – y = 3, 2x + 3y + 4z = 17.
find BA an⇒d use this to solve the system of equations y + 2z = 7, x – y = 3, 2x + 3y + 4z = 17.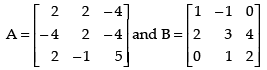
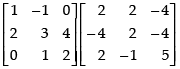
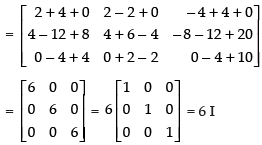
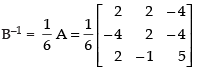
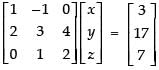

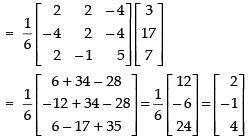
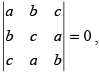 then prove that a = b = c.
then prove that a = b = c.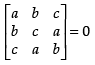
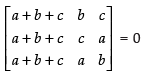
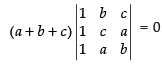 (Taking a + b + c common from C1)
(Taking a + b + c common from C1)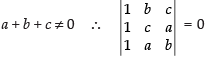
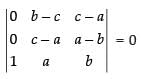
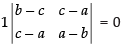
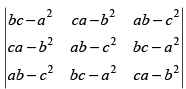 is divisible by a + b + c and find the quotient.
is divisible by a + b + c and find the quotient.