NCERT Exemplar: Application of Integrals

Q.1. Find the area of the region bounded by the curves y² = 9x, y = 3x.
Ans.
We have, y² = 9x, y = 3x
Solving the two equations, we have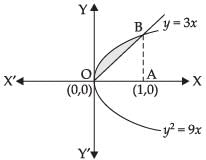

(3x)² = 9x
⇒ 9x² - 9x = 0 ⇒ 9x (x - 1) = 0
∴ x = 0, 1 Area of the shaded region
= ar (region OAB) - ar (DOAB)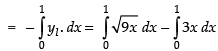


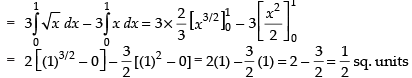
Hence, the required area =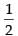sq. units.

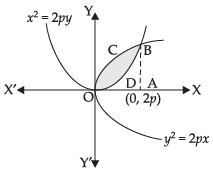
Q.2. Find the area of the region bounded by the parabola y² = 2px, and x² = 2py.
Ans.
We are given that: x² = 2py ...(i)
and y² = 2px ...(ii)
From eqn. (i) we get y =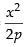

Putting the value of y in eqn. (ii) we have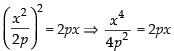

⇒ x⁴ = 8p³x ⇒ x⁴ - 8p³x = 0
⇒ x (x³ - 8p³) = 0 ∴ x = 0, 2p
Required area = Area of the region (OCBA - ODBA)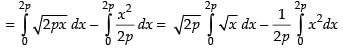



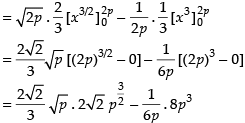
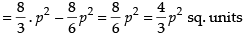
Hence, the required area =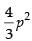sq. units.

Q.3. Find the area of the region bounded by the curve y = x³ and y = x + 6 and x = 0.
Ans.
We are given that: y = x³, y = x + 6 and x = 0
Solving y = x³ and y = x + 6, we get
x + 6 = x³
⇒ x³ - x - 6 = 0
⇒ x² (x - 2) + 2x (x - 2) + 3 (x - 2) = 0
⇒ (x - 2) (x² + 2x + 3) = 0
x² + 2x + 3 = 0 has no real roots. ∴ x = 2
∴ Required area of the shaded region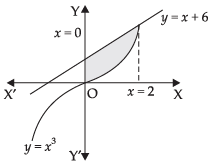


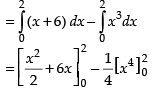
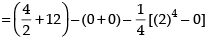
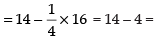10 sq. units.

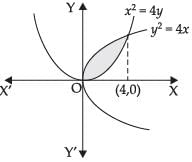
Q.4. Find the area of the region bounded by the curve y² = 4x, x² = 4y.
Ans.
We have y² = 4x and x² = 4y.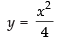

⇒

⇒
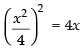
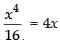
⇒ x⁴ = 64x ⇒ x⁴ - 64x = 0
⇒ x(x³ - 64) = 0
∴ x = 0, x = 4
Required area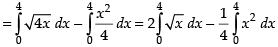


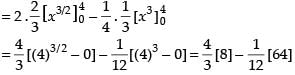
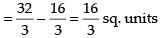
Hence, the required area =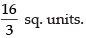

Q.5. Find the area of the region included between y² = 9x and y = x
Ans.
Given that: y² = 9x ...(i)
and y = x...(ii)
Solving eqns. (i) and (ii) we have
x² = 9x ⇒ x² - 9x = 0
x (x - 9) = 0 ∴ x = 0, 9
Required area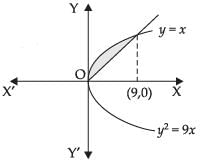





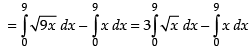
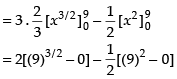
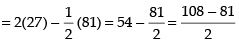
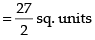
Hence, the required area =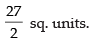

Q.6. Find the area of the region enclosed by the parabola x² = y and the line y = x + 2
Ans.
Here, x² = y and y = x + 2
∴ x² = x + 2
⇒ x² - x - 2 = 0
⇒ x² - 2x + x - 2 = 0
⇒ x(x -2) + 1 (x - 2) = 0
⇒ (x - 2) (x + 1) = 0
∴ x = -1, 2
Graph of y = x + 2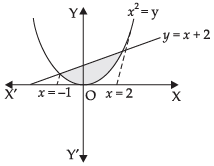


Area of the required region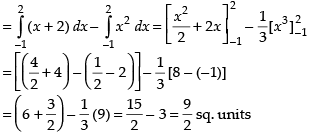

Hence, the required area =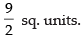

Q.7. Find the area of region bounded by the line x = 2 and the parabola y² = 8x
Ans.
Here, y² = 8x and x = 2
y² = 8(2) = 16
∴ y = ±4
Required area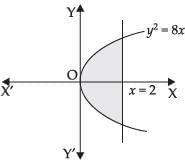



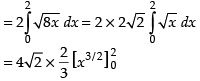
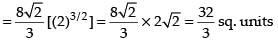
Hence, the area of the region =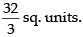

Q.8. Sketch the region {(x, 0) : y =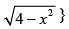and x-axis. Find the area of the region using integration.
Ans.
Given that {(x, 0) : y =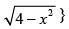 
⇒ y² = 4 - x²
⇒ x² + y² = 4 which is a circle.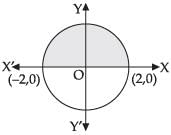

Required area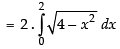

[Since circle is symmetrical about y-axis]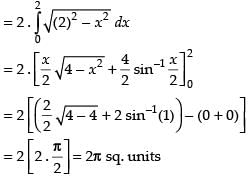

Hence, the required area = 2π sq. units.

Q.9. Calculate the area under the curve y = 2 √x included between the lines x = 0 and x = 1.
Ans.
Given the curves y = 2√x , x = 0 and x = 1.
y = 2√x ⇒ y² = 4x (Parabola)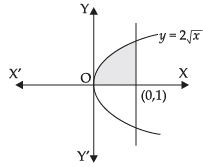

Required area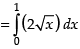

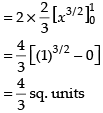
Hence, required area =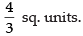

Q.10. Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8.
Ans.
Given that: 2y = 5x + 7, x-axis, x = 2 and x = 8.
Let us draw the graph of 2y = 5x + 7 ⇒ y =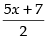


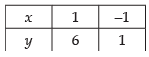
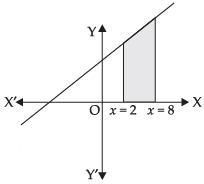
Area of the required shaded region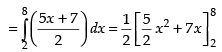

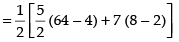
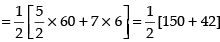
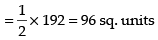
Hence, the required area = 96 sq. units.

Q.11. Draw a rough sketch of the curve y =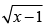in the interval [1, 5]. Find the area under the curve and between the lines x = 1 and x = 5.
Ans.
Here, we have y =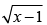 

⇒ y² = x - 1 (Parabola)
Area of the required region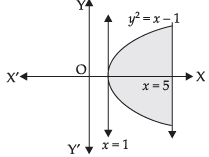



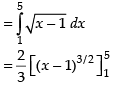
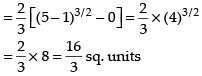
Hence, the required area =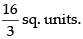

Q.12. Determine the area under the curve y =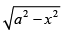 included between the lines x = 0 and x = a.
Ans.
Here, we are given y =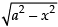

⇒ y² = a² - x²

⇒ x² + y² = a² 
Area of the shaded region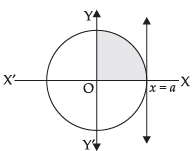



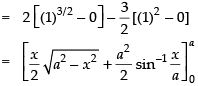
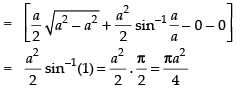
Hence, the required area =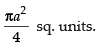

Q.13. Find the area of the region bounded by y = √x and y = x.
Ans.
We are given the equations of curve y = √x and line y = x.
Solving y = √x ⇒ y² = x and y = x, we get
x² = x ⇒ x² - x = 0
⇒ x (x - 1) = 0 ∴ x = 0, 1
Required area of the shaded region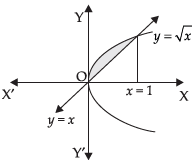



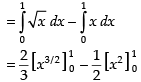
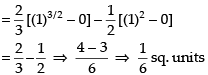
Hence, the required area =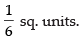

Q.14. Find the area enclosed by the curve y = -x² and the straight lilne x + y + 2 = 0.
Ans.
We are given that y = -x² or x² = -y
and the line x + y + 2 = 0
Solving the two equations, we get
x  - x² + 2 = 0
⇒ x²  - x - 2 = 0
⇒ x² - 2x + x - 2 = 0
⇒ x (x - 2) + 1 (x - 2) = 0
⇒ (x - 2) (x + 1) = 0
∴ x = -1, 2
Area of the required shaded region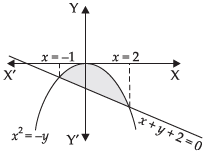


⇒
⇒
⇒
⇒

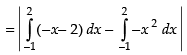
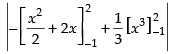
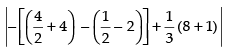
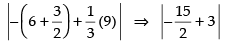
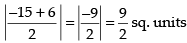
Q.15. Find the area bounded by the curve y = √x , x = 2y + 3 in the first quadrant and x-axis.
Ans.
Given that: y = √x , x = 2y + 3, first quadrant and x-axis.
Solving y = √x and x = 2y + 3, we get
y = 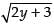 ⇒ y² = 2y + 3

⇒ y² - 2y - 3 = 0 ⇒ y² - 3y + y - 3 = 0
⇒ y(y - 3) + 1 (y - 3) = 0
⇒(y + 1) (y - 3) = 0
∴ y = -1, 3
Area of shaded region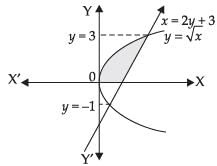



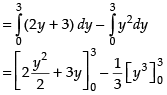
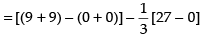
= 18 - 9 = 9 sq. units
Hence, the required area = 9 sq. units.

Long Answer (L.A.)
Q.16. Find the area of the region bounded by the curve y² = 2x and x² + y² = 4x.
Ans.
Equations of the curves are given by
x² + y² = 4x ...(i)
and y² = 2x ...(ii)
⇒ x² - 4x + y² = 0
⇒ x² - 4x + 4 - 4 + y² = 0
⇒  (x - 2)² + y² = 4
Clearly it is the equation of a circle having its centre (2, 0) and radius 2.
Solving x² + y² = 4x and y² = 2x
x² + 2x = 4x
⇒ x² + 2x - 4x = 0
⇒  x² - 2x = 0
⇒ x (x - 2) = 0
∴ x = 0, 2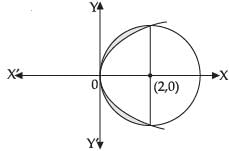

Area of the required region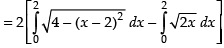

[∴ Parabola and circle both are symmetrical about x-axis.]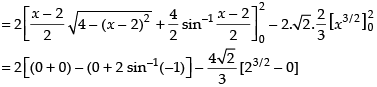


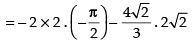
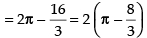sq. units
Hence, the required area =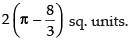

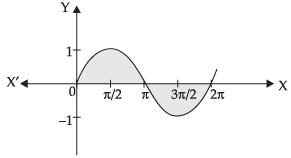
Q.17. Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
Ans.
Required area =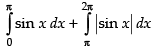




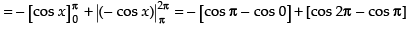
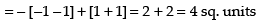
Q.18. Find the area of region bounded by the triangle whose vertices are (-1, 1), (0, 5) and (3, 2), using integration.
Ans.
The coordinates of the vertices of ΔABC are given by A(-1, 1), B (0, 5) and C (3, 2).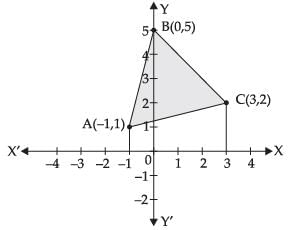

Equation of AB is y - 1 =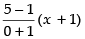
⇒ y - 1 = 4x + 4
∴ y = 4x + 4 + 1 ⇒ y = 4x + 5 ...(i)
Equation of BC is y - 5 =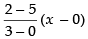
⇒ y - 5 = -x
∴ y = 5 - x ...(ii)
Equation of CA is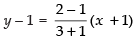

⇒
∴
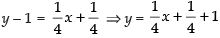
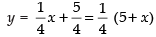
Area of ΔABC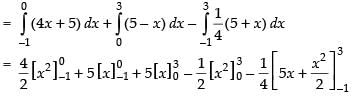






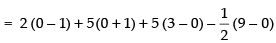
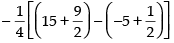
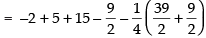
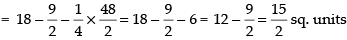
Q.19. Draw a rough sketch of the region {(x, y) : y² ≤ 6ax and x² + y² ≤ 16a²}. Also find the area of the region sketched using method of integration.
Ans.
Given that:
{(x, y) : y² ≤ 6ax and x² + y² ≤ 16a²}
Equation of Parabola is
y² = 6ax ...(i)
and equation of circle is
x² + y² ≤ 16a² ...(ii)
Solving eqns. (i) and (ii) we get
x² + 6ax = 16a²
⇒ x² + 6ax - 16a² = 0
⇒ x² + 8ax - 2ax - 16a² = 0
⇒ x(x + 8a) - 2a (x + 8a) = 0
⇒(x + 8a) (x - 2a) = 0
∴ x = 2a and x = - 8a. (Rejected as it is out of region)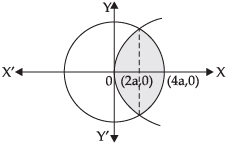

Area of the required shaded region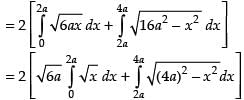






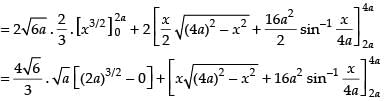
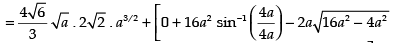
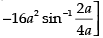
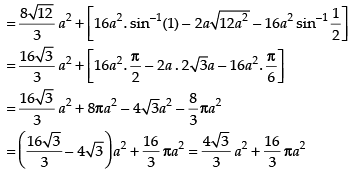
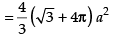
Hence, required area =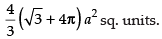

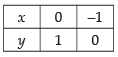
Q.20. Compute the area bounded by the lines x + 2y = 2, y - x = 1 and 2x + y = 7.
Ans.
Given that: x + 2y = 2 ...(i)
y - x = 1 ...(ii)
and 2x + y = 7 ...(iii)

Solving eqns. (ii) and (iii) we get
y = 1 + x
∴ 2x + 1 + x = 7
3x = 6
⇒ x = 2
∴ y = 1 + 2  = 3
Coordinates of B = (2, 3)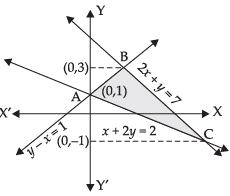

Solving eqns. (i) and (iii)
we get
x + 2y = 2
∴ x = 2 - 2y
2x + y = 7
2(2 - 2y) + y = 7
⇒ 4 - 4y + y = 7 ⇒ - 3y = 3
∴ y = -1 and x = 4
∴ Coordinates of C = (4, - 1) and coordinates of A = (0, 1).
Taking the limits on y-axis, we get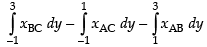




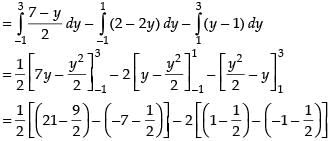
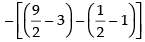
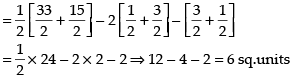
Hence, the required area = 6 sq. units.

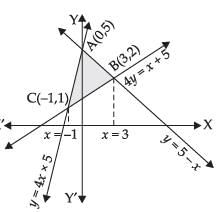
Q.21. Find the area bounded by the lines y = 4x + 5, y = 5 - x and 4y = x + 5.
Ans.
Given that y = 4x + 5 ...(i)
y = 5 - x ...(ii)
and 4y = x + 5 ...(iii)


Solving eq. (i) and (ii) we get
4x + 5 = 5 - x
⇒ x = 0 and y = 5
∴ Coordinates of A = (0, 5)
Solving eq. (ii) and (iii)
y = 5 - x
4y = x + 5
5y = 10
∴ y = 2 and x = 3
∴ Coordinates of B = (3, 2)
Solving eq. (i) and (iii)
y = 4x + 5
4y = x + 5
⇒ 4 (4x + 5) = x + 5
⇒ 16x + 20 = x + 5 ⇒ 15x = - 15
∴ x = -1 and y = 1
∴ Coordinates of C = (-1, 1).
∴ Area of required regions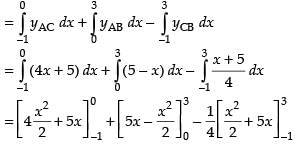



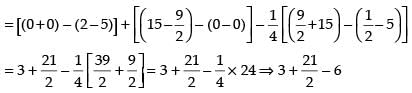
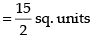
Hence, the required area =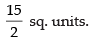

Q.22. Find the area bounded by the curve y = 2cosx and the x-axis from x = 0 to x = 2π.
Ans.
Given equation of the curve is y = 2 cos x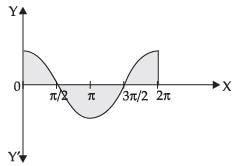

∴ Area of the shaded region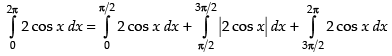





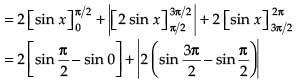
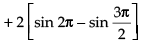
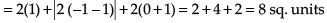
Q.23. Draw a rough sketch of the given curve y = 1 + |x +1|, x = -3, x = 3, y = 0 and find the area of the region bounded by them, using integration.
Ans.
Given equations are y = 1 + |x + 1|, x = -3
and x  = 3, y = 0
Taking y = 1 + |x + 1|
⇒ y = 1 + x + 1
⇒ y = x + 2 and y = 1 - x - 1 
⇒ y = -x
On solving we get x = -1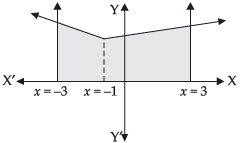

Area of the required regions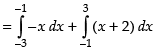


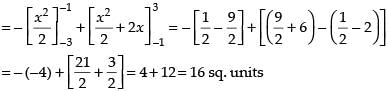
Hence, the required area = 16 sq. units.

Objective Type Questions
Q.24. The area of the region bounded by the y-axis, y = cosx and y = sinx, 0 ≤ x ≤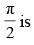
(a) √2 sq. units 
(b) ( √2 + 1) sq. units 
(c) ( √2 - 1) sq. units 
(d) (2√2 - 1) sq. units
Ans. (c)
Solution .
Given that y-axis, y = cos x, y = sin x,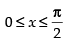 

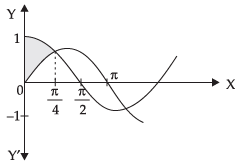
Required area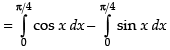

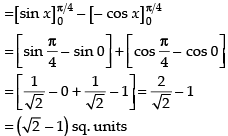
Hence, the correct option is (c).

Q.25. The area of the region bounded by the curve x² = 4y and the straight line x = 4y - 2 is
(a) 3/8 sq. units 
(b) 5/8 sq. units
(c) 7/8 sq. units
(d) 9/8 sq. units
Ans. (d)
Solution .
Given that: The equation of parabola is x² = 4y ...(i)
and equation of straight line is x = 4y - 2 ...(ii)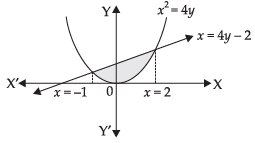

Solving eqn. (i) and (ii) we get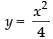


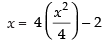
⇒ x = x² - 2
⇒ x² - x - 2 = 0 ⇒ x² - 2x + x - 2 = 0
⇒ x (x - 2) + 1 (x - 2) = 0 ⇒ (x - 2) (x + 1) = 0 ∴ x = -1, x = 2
Required area =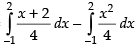

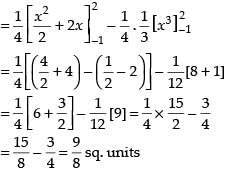
Hence, the correct option is (d).

Q.26. The area of the region bounded by the curve y =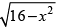and x-axis is 
(a) 8 sq units 
(b) 20π sq units  
(c) 16π sq units 
(d) 256π sq units
Ans. (a)
Solution .
Here, equation of curve is y =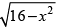 
Required area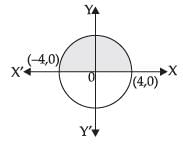


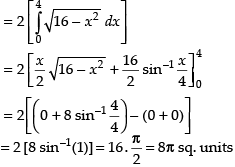
Hence, the correct option is (a).

Q.27. Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x² + y² = 32 is 
(a) 16π sq units 
(b) 4π sq units 
(c) 32π sq units    
(d) 24 sq units
Ans. (b)
Solution .
Given equation of circle is  x² + y² = 32 ⇒ x² + y² = (4√2 )²
and the line is y = x and the x-axis.
Solving the two equations we have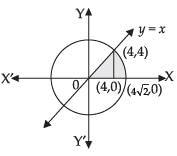

x² + x² = 32
⇒ 2x² = 32
⇒ x² = 16
∴ x = ± 4
Required area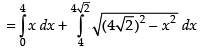



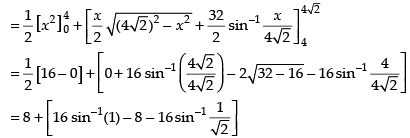
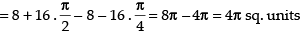
Hence, the correct option is (b).

Q.28. Area of the region bounded by the curve y = cosx between x = 0 and x = π is
(a) 2 sq. units 
(b) 4 sq. units 
(c) 3 sq. units 
(d) 1 sq. units
Ans. (a)
Solution .
Given that: y = cos x, x = 0, x = π
Required area



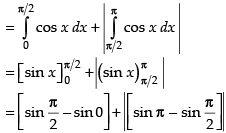
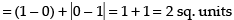
Hence, the correct option is (a).

Q.29. The area of the region bounded by parabola y² = x and the straight line 2y = x is
(a) 4/3 sq. units 
(b) 1 sq. unit
(c) 2/3 sq. units 
(d) 1/3 sq. units
Ans. (a)
Solution .
Given equation of parabola is y² = x ...(i)
and equation of straight line is 2y = x ...(ii)
Solving eqns. (i) and (ii) we get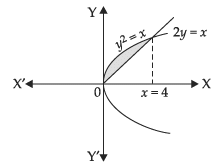


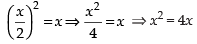
⇒ x(x - 4) = 0 ∴ x = 0, 4
Required area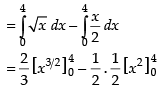



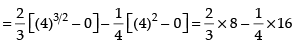
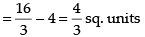
Hence, the correct answer is (a).

Q.30. The area of the region bounded by the curve y = sinx between the ordinates x = 0,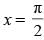and the x-axis is
(a) 2 sq. units 
(b) 4 sq. units 
(c) 3 sq. units 
(d) 1 sq. units
Ans. (d)
Solution .
Given equation of curve is y = sin x between x = 0 and x =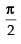

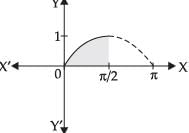
Area of required region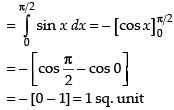

Hence, the correct answer is (d).

Q.31. The area of the region bounded by the ellipse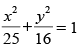 is
(a) 20π sq units 
(b) 20π² sq units 
(c) 16π² sq units 
(d) 25 π sq units
Ans. (a)
Solution .
Given equation of ellipse is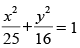 



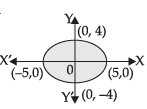
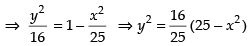
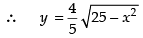
∴ Since the ellipse is symmetrical about the axes.
∴ Required area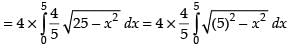

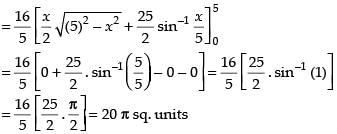
Hence, the correct answer is (a).

Q.32. The area of the region bounded by the circle x² + y² = 1 is 
(a) 2π sq units 
(b) π sq units 
(c) 3π sq units 
(d) 4π sq units
Ans. (b)
Solution .
Given equation of circle is
x² + y² = 1  y =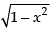

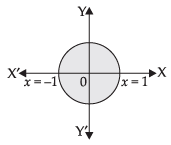
Since the circle is symmetrical about the axes.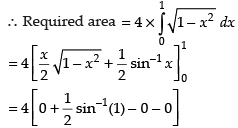


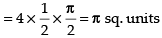
Hence, the correct answer is (b).

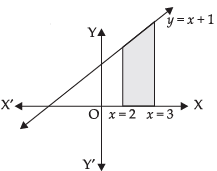
Q.33. The area of the region bounded by the curve y = x + 1 and the lines x = 2 and x = 3 is
(a) 7/2 sq. units 
(b) 9/2 sq. units 
(c) 11/2 sq. units
(d) 13/2 sq. units
Ans. (a)
Solution .
Given equation of lines are
y = x + 1, x = 2 and x = 3
Required area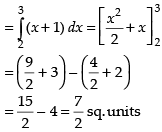


Hence, the correct option is (a).

Q.34. The area of the region bounded by the curve x = 2y + 3 and the y lines. y = 1 and y = -1 is

(a) 4 sq. units
(b) 3/2 sq. units 

(c) 6 sq. units
(d) 8 sq. units
Ans. (c)
Solution .
Given equations of lines are x = 2y + 3,  y = 1 and y = -1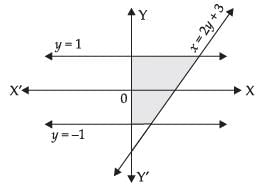

Required area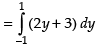

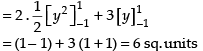
Hence, the correct answer is (c).