NCERT Exemplar - Matrices(Part-2) | Mathematics (Maths) Class 12 - JEE PDF Download
Long Answer (L.A.)
Q.49. If AB = BA for any two sqaure matrices, prove by mathematical induction that (AB)n = An Bn.
Ans.
Let P(n) : (AB)n = AnBn
Step 1:
Put n = 1, P(1) : AB = AB (True)
Step 2:
Put n = k, P(k) : (AB)k = AkBk
(Let it be true for any k ∈ N)
Step 3:
Put n = k + 1, P(k + 1) : (AB)k + 1 = Ak + 1 Bk + 1
L.H.S. (AB)k + 1 = (AB)k.AB
= AkBk.AB [from Step 2]
= Ak + 1Bk + 1 R.H.S.
L.H.S. = R.H.S.
Hence, if P(n) is true for P(k) then it is true for P(k + 1).
Q.50. Find x, y, z if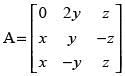 satisfies A′ = A–1.
satisfies A′ = A–1.
Ans.
Given that: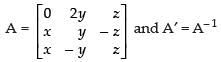
Pre-multiplying both sides by A we get,
AA′ = AA– 1
⇒ AA′ = I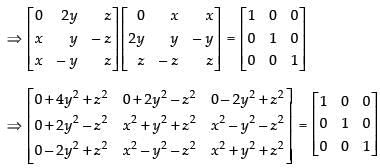
Equating the corresponding elements, we get,
4y2 + z2 = 1 ...(i)
2y2 – z2 = 0 ...(ii)
Adding (i) and (ii) we get,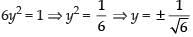
From eqn. (i), we get,
4y2 + z2 = 1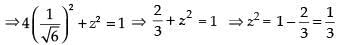
∴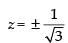
x2 + y2 + z2 = 1 ...(iii)
x2 – y2 – z2 = 0 ...(iv)
Adding (iii) and (iv) we get,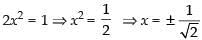
Hence,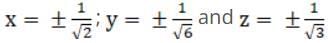
Q.51. If possible, using elementary row transformations, find the inverse of the following matrices
(i)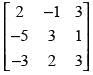
(ii)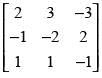
(iii)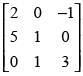
Ans.
(i) Here, A = for elementary row transformation we put
for elementary row transformation we put
A = IA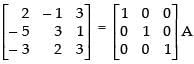
R2 → R2 + R1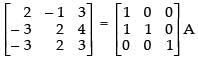
R3 → R3 - R2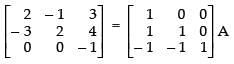
R1 → R1 + R2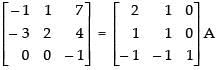
R2 → R2 - 3R1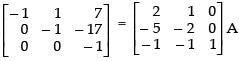
R1 → R1 + R2 and R3 → - 1 . R3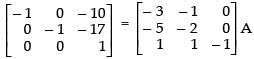
R1 → R1 + 10R3 and R2 → R2 + 17R3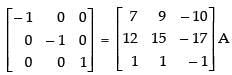
R1 → - 1. R1 and R2 → - 1. R2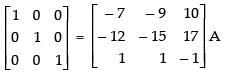
Hence,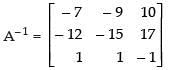
(ii) Here,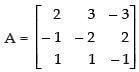
Put A = IA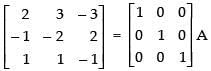
R1 → R1 - 2R3 and R2 → R2 + R1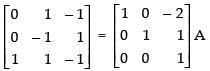
R1 → R1 + R2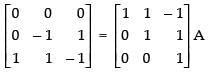
First row on L.H.S. contains all zeros, so the inverse of the given matrix A does not exist.
Hence, matrix A has no inverse.
(iii) Here,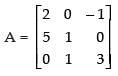
Put A = IA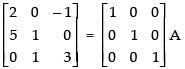
R1 → 3R1 - R2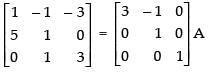
R2 → R2 - 5R1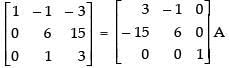
R2 → R2 - 5R3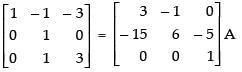
R3 → R3 - R2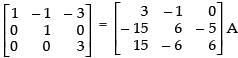
R1 → R1 + R2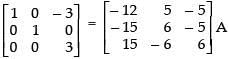
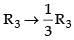
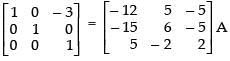
R1 → R1 + 3R3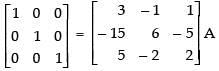
Hence,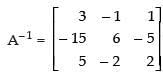
Q.52. Express the matrix as the sum of a symmetric and a skew symmetric matrix.
as the sum of a symmetric and a skew symmetric matrix.
Ans.
We know that any square matrix can be expressed as the sum of symmetric and skew symmetric matrix i.e.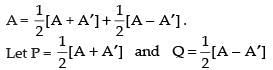
So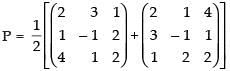
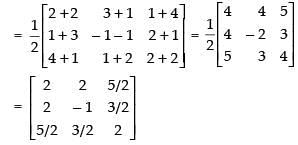

As P′ = P ∴ P is a symmetric matrix.
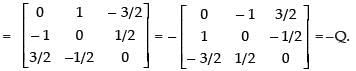
As Q = –Q ∴ Q is a skew symmetric matrix.
So A = P + Q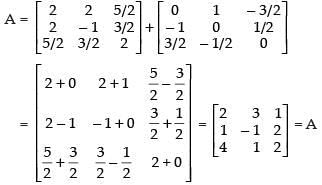
Hence, the required relation is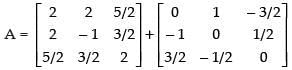
Objective Type Questions
Q.53. The matrix P =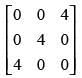 is a
is a
(a) square matrix
(b) diagonal matrix
(c) unit matrix
(d) none
Ans. (a)
Solution.
Given that A =
Here number of columns and the number of rows are equal i.e., 3.
So, A is a square matrix.
Hence, the correct option is (a).
Q.54. Total number of possible matrices of order 3 × 3 with each entry 2 or 0 is
(a) 9
(b) 27
(c) 81
(d) 512
Ans. (d)
Solution.
Total number of possible matrices of order 3 × 3 with each entry 0 or 2 = 23×3 = 29 = 512.
Hence, the correct option is (d).
Q.55. If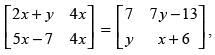 then the value of x + y is
then the value of x + y is
(a) x = 3, y = 1
(b) x = 2, y = 3
(c) x = 2, y = 4
(d) x = 3, y = 3
Ans. (b)
Solution.
Given that: 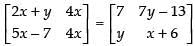
Equating the corresponding elements, we get,
2x + y = 7 ...(i)
and 4x = x + 6 ...(ii)
from eqn. (ii) 4x – x = 6
3x = 6
∴ x = 2
from eqn. (i) 2 × 2 + y = 7
4 + y = 7 ∴ y = 7 – 4 = 3
Hence, the correct option is (b).
Q.56. If A =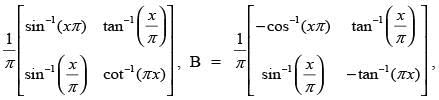 then A – B is equal to
then A – B is equal to
(a) I
(b) O
(c) 2I
(d)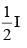
Ans. (d)
Solution.
Given that: A =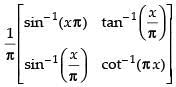 and B =
and B =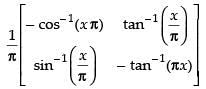
A – B = 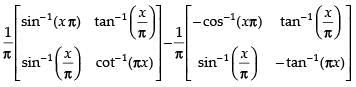
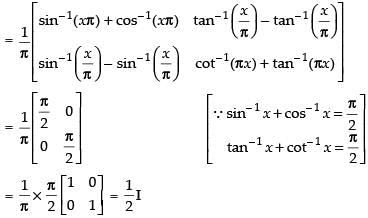
Hence, the correct option is (d).
Q.57. If A and B are two matrices of the order 3 × m and 3 × n, respectively and m = n, then the order of matrix (5A – 2B) is
(a) m × 3
(b) 3 × 3
(c) m × n
(d) 3 × n
Ans. (d)
Solution.
As we know that the addition and subtraction of two matrices is only possible when they have same order. It is also given that m = n.
∴ Order of (5A – 2B) is 3 × n
Hence, the correct option is (d).
Q.58. If A =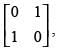 then A2 is equal to
then A2 is equal to
(a)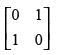
(b)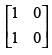
(c)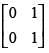
(d)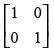
Ans. (d)
Solution.
Given that A =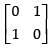
A2 = A . A =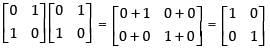
Hence, the correct option is (d).
Q.59. If matrix A = [aij]2 × 2 , where aij = 1 if i ≠ j = 0 if i = j then A2 is equal to
a) I
(b) A
(c) 0
(d) None of these
Ans. (a)
Solution.
Given that: A = [aij]2 × 2
Let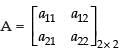 a11 = 0 [∵ i = j]
a11 = 0 [∵ i = j]
a12 = 1 [∵ i ≠ j]
a21 = 1 [∵ i ≠ j]
a22 = 0 [∵ i = j]
∴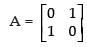
Now, A2 = A . A =
Hence, the correct option is (a).
Q.60. The matrix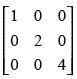 is
is
(a) Identity matrix
(b) symmetric matrix
(c) skew symmetric matrix
(d) none of these
Ans. (b)
Solution.
Let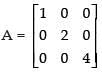
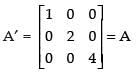
A′ = A, so A is a symmetric matrix.
Hence, the correct option is (b).
Q.61. The matrix is a
is a
(a) diagonal matrix
(b) symmetric matrix
(c) skew symmetric matrix
(d) scalar matrix
Ans. (c)
Solution.
Let 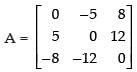
 ⇒
⇒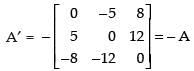
A′ = - A, so A is a skew symmetric matrix.
Hence, the correct option is (c).
Q.62. If A is matrix of order m × n and B is a matrix such that AB′ and B′A are both defined, then order of matrix B is
(a) m × m
(b) n × n
(c) n × m
(d) m × n
Ans. (d)
Solution.
Order of matrix A = m × n
Let order of matrix B be K × P
Order of matrix B′ = P × K
If AB′ is defined then the order of AB′ is m × K if n = P
If B′A is defined then order of B′A is P × n when K = m
Now, order of B′ = P × K
∴ Order of B = K × P
= m × n [∵ K = m, P = n]
Hence, the correct option is (d).
Q.63. If A and B are matrices of same order, then (AB′–BA′) is a
(a) skew symmetric matrix
(b) null matrix
(c) symmetric matrix
(d) unit matrix
Ans. (a)
Solution.
Let P = (AB′ - BA′) P′ = (AB′ - BA′)′
= (AB′)′ -(BA′)′
= (B′)A′ - (A′)′B′ [∵ (AB)′ = B′A′]
= BA′ - AB′
= –(AB′ - BA′) = -P
P′ = –P, so it is a skew symmetric matrix.
Hence, the correct option is (a).
Q.64. If A is a square matrix such that A2 = I, then (A–I)3 + (A + I)3 –7A is equal to
(a) A
(b) I – A
(c) I + A
(d) 3A
Ans. (a)
Solution.
(A – I)3 + (A + I)3 – 7A = A3 – I3 – 3A2I + 3AI2 + A3 + I3 + 3A2I + 3 AI2 – 7A
= 2A3 + 6AI2 – 7A
= 2A.A2 + 6AI – 7A
= 2AI + 6AI – 7A [A2 = I]
= 8AI – 7A = 8A – 7A
= A
Hence, the correct option is (a).
Q.65. For any two matrices A and B, we have
(a) AB = BA
(b) AB ≠ BA
(c) AB = O
(d) None of the above
Ans. (d)
Solution.
We know that for any two matrices A and B, we may have
AB = BA, AB ≠ BA and AB = 0, but it is not always true.
Hence, the correct option is (d).
Q.66. On using elementary column operations C2 → C2 – 2C1 in the following matrix equation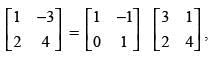 we have :
we have :
(a)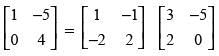
(b)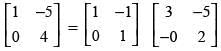
(c)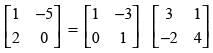
(d)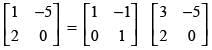
Ans. (d)
Solution.
Given that: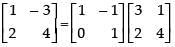
Using C2 → C2 - 2C1, we get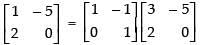
Hence, the correct option is (d).
Q.67. On using elementary row operation R1 → R1 – 3R2 in the following matrix equation: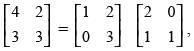 we have :
we have :
(a)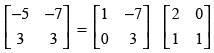
(b)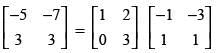
(c)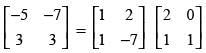
(d)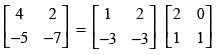
Ans. (a)
Solution.
We have,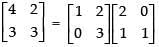
Using elementary row transformation R1 → R1 - 3R2,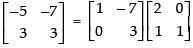
Hence, the correct option is (a).
Fill in the blanks
Q.68. _________ matrix is both symmetric and skew symmetric matrix.
Ans.
Null matrix i.e.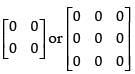 is both symmetric and skew symmetric matrix.
is both symmetric and skew symmetric matrix.
Q.69. Sum of two skew symmetric matrices is always _________ matrix.
Ans.
Let A and B be any two matrices
∴ For skew symmetric matrices
A = –A′ ...(i)
and B = –B′ ...(ii)
Adding (i) and (ii) we get
A + B = –A′ - B′
⇒ A + B = –(A′ + B′), so A + B is skew symmetric matrix.
Hence, the sum of two skew symmetric matrices is always skew symmetric matrix.
Q.70. The negative of a matrix is obtained by multiplying it by _________.
Ans.
Let A be a matrix
∴ – A = – 1 . A
Hence, negative of a matrix is obtained by multiplying it by – 1.
Q.71. The product of any matrix by the scalar _________ is the null matrix.
Ans.
Let A be any matrix
∴ 0 . A = A . 0 = 0
Hence, the product of any matrix by the scalar 0 is the null matrix.
Q.72. A matrix which is not a square matrix is called a _________ matrix.
Ans.
A matrix which is not a square matrix is called a rectangular matrix.
Q.73. Matrix multiplication is _________ over addition.
Ans.
Matrix multiplication is distributive over addition.
Let A, B and C be any matrices.
So, (i) A(B + C) = AB + AC
(ii) (A + B)C = AC + BC
Q.74. If A is a symmetric matrix, then A3 is a _________ matrix.
Ans.
Let A be a symmetric matrix
∴ A′ = A
(A3)′ = (A′)3 = A3 [∵ (A′)k = (Ak)′]
Hence, if A is a symmetric matrix, then A3 is a symmetric matrix.
Q.75. If A is a skew symmetric matrix, then A2 is a _________.
Ans.
If A is a skew symmetric matrix,
∴ A′ = –A
(A2)′ = (A′)2
= (–A)2
= A2
Hence, A2 is a symmetric matrix.
Q.76. If A and B are square matrices of the same order, then
(i) (AB)′ = _________.
(ii) (kA)′ = _________. (k is any scalar)
(iii) [k (A – B)]′ = _________.
Ans.
(i) (AB)′ = B′A′
(ii) (kA)′ = k . A′
(iii) [k(A - B)]′ = k(A - B)′ = k(A′ - B′)
Q.77. If A is skew symmetric, then kA is a _________. (k is any scalar)
Ans.
If A is a skew symmetric matrix
∴ A′ = – A
(kA)′ = kA′ = k(- A) = - kA
Hence, kA is a skew symmetric matrix.
Q.78. If A and B are symmetric matrices, then
(i) AB – BA is a _________.
(ii) BA – 2AB is a _________.
Ans.
(i) Let P = (AB – BA)
P′ = (AB – BA)′
= (AB)′ - (BA)′
= B′A′ - A′B′ [∵ (AB)′ = B′A′]
= BA – AB [∵ A′ = A and B′ = B]
= -(AB - BA)
= –P
Hence, (AB – BA) is a skew symmetric matrix.
(ii) Let Q = (BA – 2AB)
Q′ = (BA – 2AB)′
= (BA)′ - (2AB)′
= A′B′ - 2(AB)′ [∵ (kA)′ = kA′]
= A′B′ - 2B′A′
= AB – 2BA [∵ A′ = A and B′ = B]
= - (2BA - AB)
Hence, (BA – 2AB) is neither a symmetric nor a skew symmetric matrix.
Q.79. If A is symmetric matrix, then B′AB is _________.
Ans.
If A is a symmetric matrix
∴ A′ = A
Let P = B′AB
P′ = (B′AB)′
= B′A′(B′)′ [∵ (AB)′ = B′A′]
= B′AB [∵ A′ = A and (B′)′ = B]
∴ P′ = P
So, P is a symmetric matrix.
Hence, B′AB is a symmetric matrix.
Q.80. If A and B are symmetric matrices of same order, then AB is symmetric if and only if _________.
Ans.
Given that A′ = A
and B′ = B
Let P = AB
P′ = (AB)′
= B′A′
P′ = BA [∵ A′ = A and B′ = B]
= P
Hence, AB is symmetric if and only if AB = BA.
Q.81. In applying one or more row operations while finding A–1 by elementary row operations, we obtain all zeros in one or more, then A–1 _________.
Ans.
A–1 does not exist if we apply one or more row operations while finding A–1 by elementary row operations, obtain all zeroes in one or more rows.
True or False
Q.82. A matrix denotes a number.
Ans. False.
A matrix is an array of elements, numbers or functions having rows and columns.
Q.83. Matrices of any order can be added.
Ans. False.
The matrices having same order can only be added.
Q.84. Two matrices are equal if they have same number of rows and same number of columns.
Ans. False.
The two matrices are said to be equal if their corresponding elements are same.
Q.85. Matrices of different order can not be subtracted.
Ans. True.
For addition and subtraction, the order of the two matrices should be same.
Q.86. Matrix addition is associative as well as commutative.
Ans. True.
If A, B and C are the matrices of addition then
A + (B + C) = (A + B) + C (associative)
A + B = B + A (commutative)
Q.87. Matrix multiplication is commutative.
Ans. False.
Since AB ≠ BA if AB and BA are well defined.
Q.88. A square matrix where every element is unity is called an identity matrix.
Ans.
False.
Since, in identity matrix all the elements of principal diagonal are unity rest are zero.
e.g.,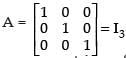
Q.89. If A and B are two square matrices of the same order, then A + B = B + A.
Ans. True.
If A and B are square matrices then their addition is commutative i.e., A + B = B + A.
Q.90. If A and B are two matrices of the same order, then A – B = B – A.
Ans. False.
Since subtraction of any two matrices of the same order is not commutative i.e.,
A – B ≠ B - A.
Q.91. If matrix AB = O, then A = O or B = O or both A and B are null matrices.
Ans. False.
Since for any two non-zero matrices A and B, we may get AB = 0.
Q.92. Transpose of a column matrix is a column matrix.
Ans. False.
Transpose of a column matrix is a row matrix.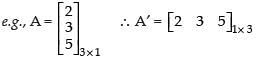
Q.93. If A and B are two square matrices of the same order, then AB = BA.
Ans. False.
For two square matrices A and B, AB = BA is not always true.
Q.94. If each of the three matrices of the same order are symmetric, then their sum is a symmetric matrix.
Ans. True.
Let A, B and C be three matrices of the same order.
Given that A′ = A, B′ = B and C′ = C
Let P = A + B + C
⇒ P′ = (A + B + C)′
= A′ + B′ + C′
= A + B + C
= P
So, A + B + C is also a symmetric matrix.
Q.95. If A and B are any two matrices of the same order, then (AB)′ = A′B′.
Ans. False.
Since (AB)′ = B′A′.
Q.96. If (AB)′ = B′ A′, where A and B are not square matrices, then number of rows in A is equal to number of columns in B and number of columns in A is equal to number of rows in B.
Ans. True.
Let A = [aij]m × n and B = [bij]p × q
AB is defined when n = P
∴ Order of AB = m × q
⇒ Order of (AB)′ = q × m
Order of B′ is q × p and order of A′ is n × m
∴ B′A′ is defined when P = n
and the order of B′A′ is q × m
Hence, order of (AB)′ = Order of B′A′ i.e., q × m.
Q.97. If A, B and C are square matrices of same order, then AB = AC always implies that B = C.
Ans. False.
Let A =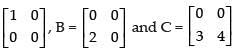
∴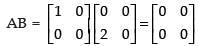
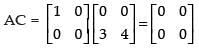
Here AB = AC = 0 but B ≠ C.
Q.98. AA′ is always a symmetric matrix for any matrix A.
Ans. True.
Let
P = AA′
P′ = (AA′)′
= (A′)′ . A′ [(AB)′ = B′A′]
= AA′
= P
So, P is symmetric matrix.
Hence, AA′ is always a symmetric matrix.
Q.99. If A =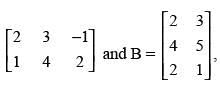 then AB and BA are defined and equal.
then AB and BA are defined and equal.
Ans. False.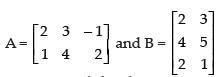
Since AB is defined∴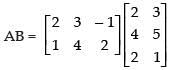
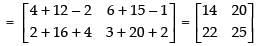
BA is also defined.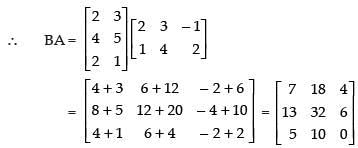
So AB ≠ BA
Q.100. If A is skew symmetric matrix, then A2 is a symmetric matrix.
Ans. True.
(A2)′ = (A′)2
= [– A]2 [∵ A′ = - A]
= A2
So, A2 is a symmetric matrix.
Q.101. (AB)–1 = A–1. B–1, where A and B are invertible matrices satisfying commutative property with respect to multiplication.
Ans. True.
If A and B are invertible matrices of the same order
∴ (AB)–1 = (BA)–1 [∵ AB = BA]
But (AB)–1 = A–1B–1 [Given]
∴ (BA)–1 = B–1A–1
So A–1B–1 = B–1A–1
∴ A and B satisfy commutative property w.r.t. multiplication.
|
203 videos|377 docs|167 tests
|
FAQs on NCERT Exemplar - Matrices(Part-2) - Mathematics (Maths) Class 12 - JEE
| 1. What are matrices and how are they used in mathematics? |  |
| 2. How can matrices be represented and manipulated in computer programming? |  |
| 3. What is the significance of the determinant of a matrix? |  |
| 4. How can matrices be used to solve systems of linear equations? |  |
| 5. Can matrices be used to solve real-world problems? |  |
















