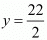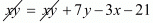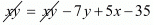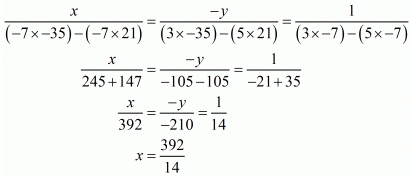Page No 3.102
Q.11. Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Ans. Let the speed of the train be x km/hour that of the bus be y km/hr, we have the following cases
Case I: When Roohi travels 300 Km by train and the rest by bus
Time taken by Roohi to travel 60 Km by train =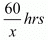
Time taken by Roohi to travel (300-60) =240 Km by bus =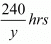
Total time taken by Roohi to cover 300Km =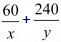
It is given that total time taken in 4 hours
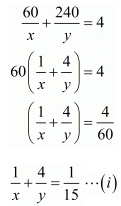
Case II: When Roohi travels 100 km by train and the rest by bus
Time taken by Roohi to travel 100 Km by train =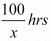
Time taken by Roohi to travel (300-100) =200Km by bus =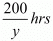
In this case total time of the journey is 4 hours 10 minutes
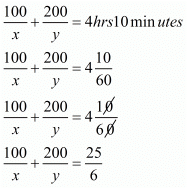
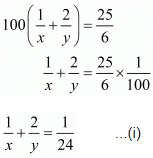
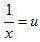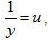Puttingand, the equations (i) and (ii) reduces to
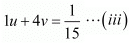
Subtracting equation (iv) from (iii) we get
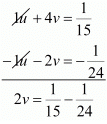
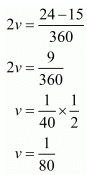
Putting 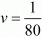in equation (iii), we get
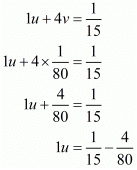
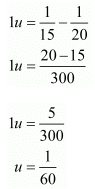
Now
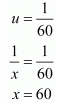
and
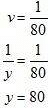
Hence, the speed of the train is 60 km / hr,
The speed of the bus is 80 km / hr.
Q.12. Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.
Ans. Let the speed of rowing in still water be x km/hr and the speed of the current be y km/hr
Speed upstream = (x - y)km / hr
Speed downstream = (x + y)km / hr
Now,
Time taken to cover 20 km down stream =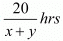
Time taken to cover 4 km upstream =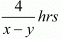
But, time taken to cover 20 km downstream in 2 hours
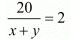
20 = 2(x + y)
20 = 2x + 2y...(i)
Time taken to cover 4 km upstream in 2 hours
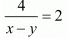
4 = 2(x - y)
4 = 2x - 2y ...(i)
By solving these equation (i) and (ii) we get
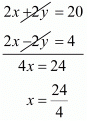
x = 6
Substitute x = 6 in equation (i) we get
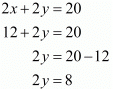
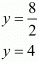
Hence, the speed of rowing in still water is 6 km / hr
The speed of current is 4 km /hr
Q.13. A motor boat can travel 30 km upstream and 28 km downstream in 7 hours. It can travel 21 km upstream and return in 5 hours. Find the speed of the boat in still water and the speed of the upstream.
Ans. Let the speed of the boat in still water be x km/h and the speed of the stream be y km/h.
Speed of boat upstream = x − y
Speed of boat downstream = x + y
It is given that, the boat travels 30 km upstream and 28 km downstream in 7 hours.
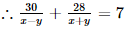
Also, the boat travels 21 km upstream and return in 5 hours.
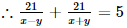
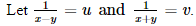
So, the equation becomes
30u + 28v = 7 ...(i)
21u + 21v = 5 ...(ii)
Multiplying (i) by 21 and (ii) by 30, we get
630u + 558v = 147 ...(iii)
630u + 630v = 150 ...(iv)
Solving (iii) and (iv), we get
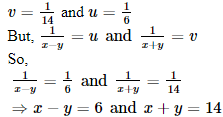
Solving these two equations, we get
x = 10 and y = 4
So, the speed of boat in still water = 10 km/h and speed of stream = 4 km/h.
Q.14. Abdul travelled 300 km by train and 200 km by taxi, it took him 5 hours 30 minutes. But if he travels 260 km by train and 240 km by taxi he takes 6 minutes longer. Find the speed of the train and that of the taxi.
Ans. Let the speed of the train be x km/hour that of the taxi be y km/hr, we have the following cases
Case I: When Abdul travels 300 Km by train and the 200 Km by taxi
Time taken by Abdul to travel 300 Km by train =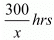
Time taken by Abdul to travel 200 Km by taxi =
Total time taken by Abdul to cover 500 Km =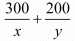
It is given that total time taken in 5 hours 30 minutes
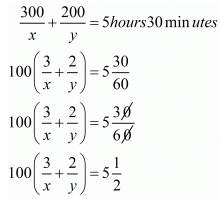
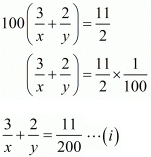
Case II: When Abdul travels 260 Km by train and the 240 km by taxi
Time taken by Abdul to travel 260 Km by train =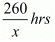
Time taken by Abdul to travel 240 Km by taxi =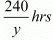
In this case total time of the journey is 5 hours 36 minutes
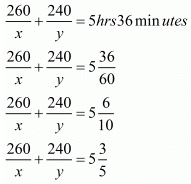
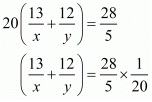
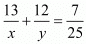...(ii)
Putting 1/x = u and, 1/y = u, the equations (i) and (ii) reduces to
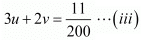
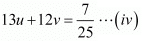
Multiplying equation (iii) by 6 the above system of equation becomes
Subtracting equation (iv) from (v) we get
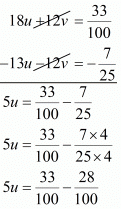
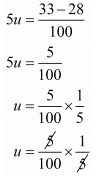
u = 1/100
Putting u = 1/100 in equation (iii), we get
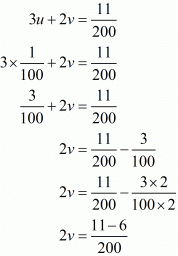
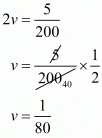
Now
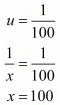
and
v = 1/ 80
1/y = 1/80
y = 80
Hence, the speed of the train is 100 km/hr.
The speed of the taxi is 80 km/hr.
Q.15. A train covered a certain distance at a uniform speed. If the train could have been 10 km/hr. faster, it would have taken 2 hours less than the scheduled time. And, if the train were slower by 10 km/hr; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
Ans. Let the actual speed of the train be 1 km/hr and the actual time taken by y hours. Then,
Distance = Speed x Time
Distance covered = (xy)km ...(i)
If the speed is increased by 10 Km/hr, then time of journey is reduced by 2 hours
when speed is (x + 10) km/ hr, time of journey is (y - 2)hours
∴ Distance covered = (x + 10)(y - 2)
xy = (x + 10)(y - 2)
xy = xy + 10y - 2x - 20
- 2x + 10y - 20 = 0
- 2x + 3y - 12 = 0 ...(ii)
When the speed is reduced by 10 km /hr, then the time of journey is increased by 3 hours when speed is (x - 10) km / hr, time of journey is (y + 3) hours
∴ Distance covered = (x - 10)(y + 3)
xy = (x - 10)(y + 3)
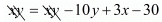
0 = -10y + 3x - 30
3x - 10y - 30 = 0 ...(iii)
Thus, we obtain the following system of equations:
- x + 5y - 10 = 0
3x - 10y - 30 = 0
By using cross multiplication, we have
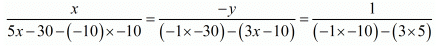
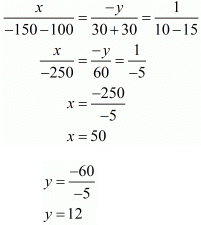
Putting the values of x and y in equation (i), we obtain
Distance= xy km
= 50 x 12
= 600 km
Hence, the length of the journey is 600 km
Q.16. Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of two cars.
Ans. Let x and y be two cars starting from points A and B respectively.
Let the speed of the car X be x km/hr and that of the car Y be y km/hr.
Case I: When two cars move in the same directions:
Suppose two cars meet at point Q, then,
Distance travelled by car X=AQ
Distance travelled by car Y=BQ
It is given that two cars meet in 5 hours.
Distance travelled by car X in 5 hours = 5x km AQ = 5x
Distance travelled by car Y in 5 hours = 5y km BQ = 5y
Clearly AQ-BQ = AB 5x - 5y = 100
Both sides divided by 5, we get x - y = 20 ...(i)
Case II: When two cars move in opposite direction
Suppose two cars meet at point P, then,
Distance travelled by X car X=AP
Distance travelled by Y car Y=BP
In this case, two cars meet in 1 hour
Therefore,
Distance travelled by car y in1 hours = 1x km
Distance travelled by car y in 1 hours = 1y km
AP + BP = AB
1x + 1y = 100
x + y = 100
x + y = 100 ...(ii)
By solving (i) and (ii) we get,
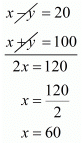
By substituting x = 60 in equation (ii), we get
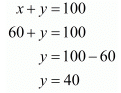
Hence, speed of car X is 60 km / hr, speed of car Y is 40 km / hr.
Q.17. While covering a distance of 30 km. Ajeet takes 2 hours more than Amit. If Ajeet doubles his speed, he would take 1 hour less than Amit. Find their speeds of walking.
Ans. Let the speed of Ajeet and Amit be x Km/hr respectively. Then,
Time taken by Ajeet to cover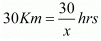
Time taken by Amit to cover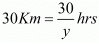
By the given conditions, we have
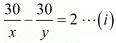
If Ajeet doubles his speed, then speed of Ajeet is 2xKm / hr
Time taken by Ajeet to cover
Time taken by Amit to cover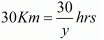
By the given conditions, we have
If Ajeet doubles his speed, then speed of Ajeet is 2xKm / hr
Time taken by Ajeet to cover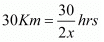
Time taken by Amit to cover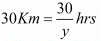
According to the given condition, we have
Putting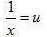andin equation (i) and (ii), we get
30u - 30v = 2 ...(iii)
- 15u + 30v = 1 ...(iv)
Adding equations (iii) and (iv), we get
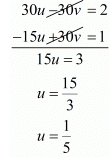
Putting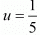in equation (iii), we get
30u - 30v = 2
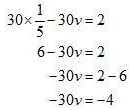
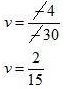
Now,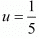
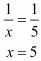
and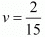
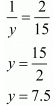
Hence, the speed of Ajeet is 5 km/ hr
The speed of Amit is 7.5 km /hr
Q.18. A takes 3 hours more than B to walk a distance of 30 km. But, if A doubles his pace (speed) he is ahead of B by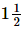hours. Find the speeds of A and B.
Ans. Let the speed of A and B be x Km/hr and y Km/hr respectively. Then,
Time taken by A to cover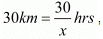
And, Time taken by B to cover
By the given conditions, we have
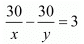
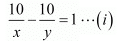
If A doubles his pace, then speed of A is 2x km / hr
Time taken by A to cover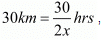
Time taken by B to cover
According to the given condition, we have
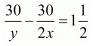
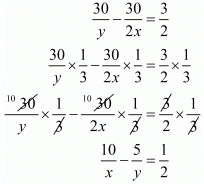
...(ii)
Putting 1/x = u and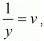in equation (i) and (ii), we get
10u - 10v = 1
10u - 10v - 1 = 0 ...(iii)
- 10u + 20v = 1
- 10u + 20v - 1 = 0 ...(iv)
Adding equations (iii) and (iv), we get,
10v - 2 = 0
10v = 2
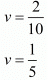
Putting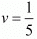in equation (iii), we get
10u - 10v - 1= 0
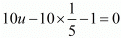
10u - 2 - 1 = 0
10u - 3 = 0
10u = 3
u = 3/10
Now, u = 3/10
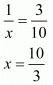
and,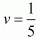
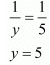
Hence, the A’s speed is,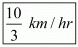
The B’s speed is 5 km / hr.
Page No 3.111
Q.1. If in a rectangle, the length is increased and breadth reduced each by 2 units, the area is reduced by 28 square units. If, however the length is reduced by 1 unit and the breadth increased by 2 units, the area increases by 33 square units. Find the area of the rectangle.
Ans. Let the length and breadth of the rectangle be x and y units respectively
Then, area of rectangle = xy square units
If length is increased and breadth reduced each by 2 units, then the area is reduced by 28 square units
(x + 2) (y - 2) = xy - 28
⇒ xy - 2x + 2y - 4 = xy - 28
⇒ -2x + 2y - 4 + 28 = 0
⇒ -2x + 2y + 24 = 0
⇒ 2x - 2y - 24 = 0
Therefore, 2x - 2y - 24 = 0 ...(i)
Then the length is reduced by 1 unit and breadth is increased by 2 units then the area is increased by 33 square units
(x − 1) (y + 2) = xy + 33
⇒ xy + 2x − y − 2 = xy + 33
⇒ 2x − y −2 − 33 = 0
⇒ 2x − y − 35 = 0
Therefore, 2x − y − 35 = 0 .....(ii)
Thus we get the following system of linear equation
2x − 2y − 24 = 0
2x − y − 35 = 0
By using cross multiplication, we have
x = 23
and
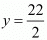
y = 11
The length of rectangle is 23 units.
The breadth of rectangle is 11 units.
Area of rectangle =length x breadth,
= x x y
= 23 x 11
= 253 square units
Hence, the area of rectangle is 253 square units.
Q.2. The area of a rectangle remains the same if the length is increased by 7 meters and the breadth is decreased by 3 meters. The area remains unaffected if the length is decreased by 7 meters and breadth in increased by 5 meters. Find the dimensions of the rectangle.
Ans. Let the length and breadth of the rectangle be x and y units respectively
Then, area of rectangle = xy square units
If length is increased by 7 meters and breadth is decreased by 3 meters when the area of a rectangle remains the same
Therefore,
xy = (x + 7) (y - 3)
xy = xy + 7y - 3x - 21
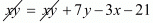
3x - 7y + 21 = 0 ...(i)
If the length is decreased by 7 meters and breadth is increased by 5 meters when the area remains unaffected, then
xy = (x - 7) (y + 5)
xy = xy - 7y + 5x - 35
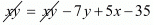
0 = 5x - 7y - 35 ...(ii)
Thus we get the following system of linear equation
3x - 7y + 21 = 0
5x - 7y - 35 = 0
By using cross-multiplication, we have
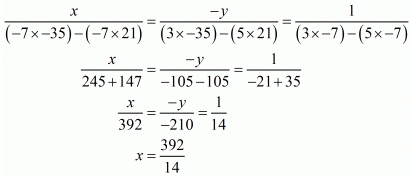
x = 28
and
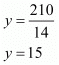
Hence, the length of rectangle is 28 meters
The breadth of rectangle is 15 meters.
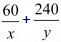
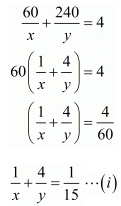
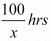
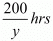
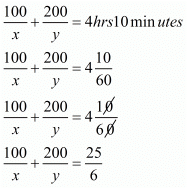
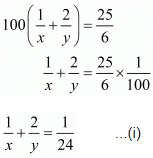
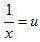and,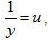
the equations (i) and (ii) reduces to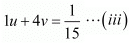
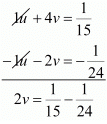
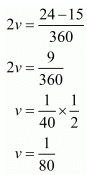
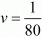in equation (iii), we get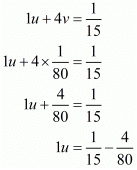
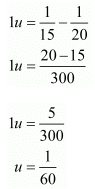
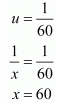
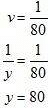
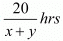
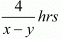
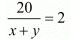
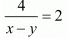
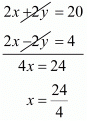
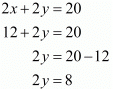
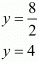
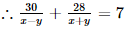
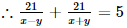
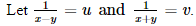
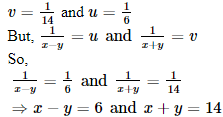
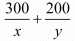
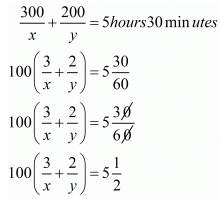
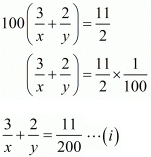
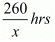
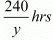
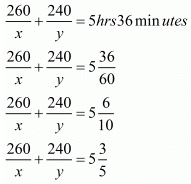
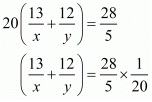
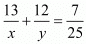...(ii)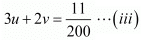
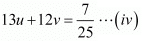
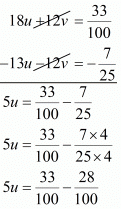
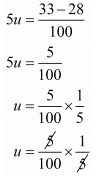
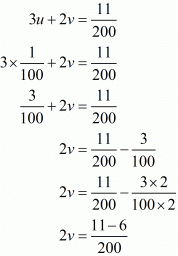
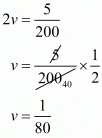
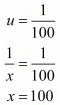
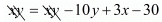
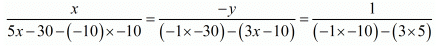
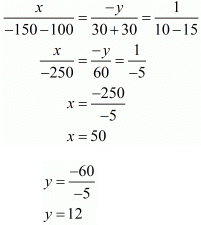
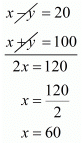
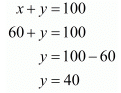
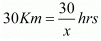
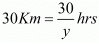
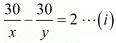
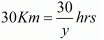
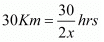
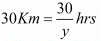
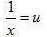and
in equation (i) and (ii), we get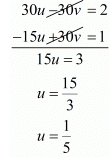
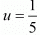in equation (iii), we get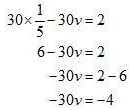
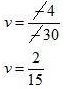
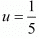
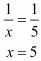
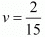
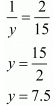
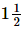hours. Find the speeds of A and B.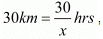
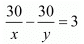
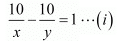
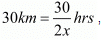
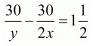
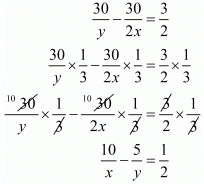
...(ii)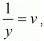
in equation (i) and (ii), we get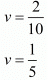
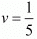in equation (iii), we get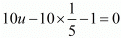
,
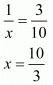
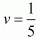
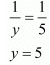
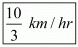