Important Formula: Remainder & Divisibility | Quantitative Aptitude (Quant) - Interview Preparation PDF Download
| Table of contents |

|
| Introduction |

|
| Theorems of Divisibility |

|
| Factors |

|
| Factors Formulas |

|
| Prime Factorisation |

|
| Divisibility Rules |

|
| Solved Questions: Factors |

|
Introduction
A number 'x' is said to be completely divisible by another number ‘y’ if it leaves no remainder.
- In general, it can be said that any integer I, when divided by a natural number N, there exist a unique pair of numbers Q and R which are called the Quotient and Remainder, respectively.
Thus, I = QN + R, where Q is an integer and N is a natural number or zero, and 0 < R < N (i.e. remainder has to be a whole number less than N).

- If the remainder is zero, we say that the number I is divisible by N.
- When R > 0, we say that the number I is divisible by N with a remainder.
Example: 25/8 can be written as: 25 = 3 * 8 + 1, where 3 is the quotient and 1 is the remainder. - Suppose, we divide – 32 by 7. Contrary to what you might expect, the remainder, in this case, is + 3 (and not – 4). This is because the remainder is always non-negative. Thus, –32/7 gives quotient as – 5 and remainder as + 3.
Example: –25/7 can be written as –25 = 7 * (-4) + 3, where -4 is the quotient and 3 is the remainder.
Theorems of Divisibility
 Some common divisibility rules
Some common divisibility rules1. If a is divisible by b, then a is divisible by bc for all c.
2. If a is divisible by b and b is divisible by c, then a is divisible by c.
3. If a and b are natural numbers such that a is divisible by b and b is divisible by a, then a = b.
4. If n is divisible by d and m is divisible by d then (m + n) and (m – n) are both divisible by d.
This has an important implication.
Suppose 28 and 742 are both divisible by 7.
Then (742 + 28) as well as (742 – 28) are divisible by 7. (and in fact so is + 28 – 742).
5. If a is divisible by b and c is divisible by d then ac is divisible by bd.
6. The highest power of a prime number p, which divides n! exactly is given by [n/p] + [n/p2] + [n/p3] +... where [x] denotes the greatest integer less than or equal to x.
Factors
A factor of a number can be defined as a number that divides the given number without leaving any remainder.
Generally, factors based questions are of the following types:
(i) The number of factors.
(ii) The sum of factors.
(iii) Product of factors.
(iv) Odd and Even Factors.
(v) Number of Factors which are perfect squares for certain kinds of questions.
Factors Formulas
There are basically three types of formulas considered for factors. They are:
- Number of Factors
- Product of Factors
- Sum of Factors
Let us assume N is a natural number, for which we need to find the factors. If we convert N into the product of prime numbers by the prime factorization method, we can represent it as;
N = Xa × Yb × Zc
where X, Y and Z are the prime numbers and a, b and c are their respective powers.
(i) Number of Factors
The formula for the total number of factors for a given number is given by:
Total Number of Factors for N = (a+1) (b+1) (c+1) |
(ii) Sum of Factors
The formula for the sum of all factors is given by:
| Sum of factors of N = [(Xa+1-1)/X-1] × [(Yb+1-1)/Y-1] × [(Zc+1-1)/Z-1] |
(iii) Product of Factors
The formula for the product of all factors is given by:
Product of factors of N = NTotal No. of Factors/2 |
Prime Factorisation
We all know that every composite number can be written as a product of some prime numbers.
For example: We can write 90 as 2 × 32 × 5.
This process is called prime factorization, and it is the first step to solve any questions related to factors.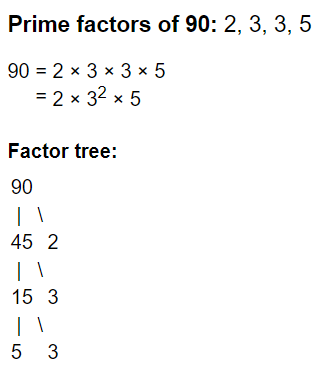 Prime Factors of 90Number of Factors of a Number
Prime Factors of 90Number of Factors of a Number
- Factors are those numbers that divide the given number completely.
Example: Factors of 72 - 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 48 and 72. - Observe that the number 1 is always a factor of every number, and the number itself will be the factor of the number.
- Now let us understand the formula for finding the number of factors of any composite number. We will take the above example of 72.
72 = 23 × 32 Prime Factors of 72
Prime Factors of 72 - Clearly, the number 72 is divisible by each of 20,21, 22, 23... but not by any higher power of 2 like 24, 25, … . Similarly, the number 72 is divisible by each of 30, 31, 32,..... but not by 33,34,….
- We should also observe that the number can be divisible by any ‘combination’ of one of 20,21, 22, 23 and one of 30, 31, 32.....by numbers of type 21 × 32 or 22 × 31 and so on.
How to Find the Sum of Factors of a Number?
- You might have encountered with such questions in earlier CAT papers or any Test series. Well, questions of such types require prior knowledge of solving it. Otherwise, you will waste time trying to solve such questions and end up with no results.
- There is a complete algorithm to solve such questions.
- Example: Find the sum and number of Factors of 720.
Sol: Write the number in Standard Form i.e. 720 = 24 x 32 x 51
Create a number of brackets as the number of prime factors.
Fill each bracket with the sum of all the powers of the respective prime number starting from 0 to the highest power of that number.
Sum of the factors = (20 + 21 + 22 + 23 + 24) x (30 + 31 + 32) x (50 + 51)
= (1 + 2 + 4+ 8 +16) x (1 + 3 + 9) x (1+ 5)
= 31 x 13 x 6 = 2418
How to Find Number of Factors of a Number?
- If you will check the sum of factors in step 3, and expand the bracket, you will find that all are actually factors of the number.
- Lets take a small number for this say 80:
80 = 24 x 51
Sum of the factors = (20 + 21 + 22 + 23 + 24) x (50 + 51) = 31 x 6 = 186 - So to calculate the number of factors of 80:
Add 1 to the powers of prime factors and multiply it
No. of Factors of 80 = (4 + 1) x (1 + 1) = 10. - Example: Find the number of Factors of 720.
Sol: 720 = 24 x 32 x 51
Number of Factors of 720 = (4 + 1) x (2 + 1) x (1 + 1) = 5 x 3 x 2 = 30
Divisibility Rules
As the name suggests, divisibility rules or tests are the procedures used to check whether a number is divisible by another number without necessarily performing the actual division.
 Divisibility Rules
Divisibility Rules
➤ Divisibility Test for 1
The divisibility test for 1 does not have any condition for numbers. All numbers are divisible by 1 irrespective of how large the numbers are.
When any number is divided by 1, the result is the number itself.
Example: 5/1= 5 and 100000/1 = 100000.
➤ Divisibility Test for 2
A number is divisible by 2 if the last digit of the number is 2, 4, 6, 8 or 0.
Example: 102/2 = 51, 54/2 = 27, 66/2 = 33, 28/2 = 14 and 20/2 = 10
Example. Check if 288 is divisible by 2.
Ans: Given, 288 is a number.
If the last digit of 288 is divisible by 2, then 288 is also divisible by 2.
The last digit of 288 is 8, which is divisible by 2, such that;
8/2 = 4
Hence, 288 satisfy the divisibility rule for 2.
➤ Divisibility Test for 3
The divisibility test for 3 states that a number is completely divisible by 3 if the digits of the number are divisible by 3 or is a multiple of 3.
 Divisibility Rule of 3
Divisibility Rule of 3
Example: Consider two numbers 308 and 207.
(i) Check 308 by summing its digits: 3 + 0 + 8 = 11, since 11 is not divisible by 3, then 308 is also not divisible by 3.
(ii) Check 207 by summing its digits: 2 + 0 + 7 = 9, since 9 is a multiple of 3, then 207 is also divisible by 3.
➤ Divisibility Test for 4
The divisibility test for 4 states that a number is divisible by 4 if the last two digits of the number are divisible by 4.
 Divisibility Rule of 4
Divisibility Rule of 4
Example: Consider two numbers, 2508 and 2506.
(i) 2508 is divisible by 4 because the last two digits 08 are divisible by 4.
(ii) 2506 is not divisible by 4 because the last two digits 06 are not divisible by 4.
Q. Check if 195 is divisible by 4 or not.
Solution: As we can see, the last digit of 195 is 5, which is not divisible by 4.
Hence, 195 is not divisible by 4.
➤ Divisibility Test for 5
- All numbers with the last digit as 0 or 5 are divisible by 5.
Example: 100/5 = 20, 205/5 = 41.
➤ Divisibility Test for 6
A number is divisible by 6 if its last digit is an even number or zero and the sum of the digits is a multiple of 3.

Example: 270 is divisible by 2 because the last digit is 0 and the sum of the digits is: 2 + 7 + 0 = 9 which is also divisible by 3.
Therefore, 270 is divisible by 6.
➤ Divisibility Rules for 7
- The divisibility test of 7 is explained in the following algorithm Consider a number 1073.
- To check whether the number is divisible by 7 or not? Eliminate number 3 and multiply it by 2, which becomes 6.
- Subtract 6 from the remaining number 107, therefore 107 – 6 = 101. Repeat again the process we have 1 x 2 = 2, and the remaining number is 10 – 2 = 8.
Since 8 is not divisible by 7, therefore the number 1073 is also not divisible by 7.
➤ Divisibility Test for 8
The divisibility test for 8 states that a number is divisible by 8 if its last three digits are divisible by 8.
 Divisibility Rule of 8
Divisibility Rule of 8
➤ Divisibility Test for 9
The divisibility test for 9 is the same as the divisibility test for 3. If the sum of the digits of a number is divisible by 9, then the number is also divisible by 9.
 Divisibility Rule of 9
Divisibility Rule of 9
Example: In a number like 78532, the sum of its digits is: 7+8+5+3+2 = 25.
- Since 25 is not divisible by 9, the 78532 is also not divisible by 9. Considering another case of number: 686997, the sum of digits is: 6 + 8 + 6 + 9 + 9 + 7 = 45. Since the sum is divisible by 9, then the number 686997 is divisible by 9.
➤ Divisibility Test for 10
- The divisibility rule for 10 states that any number whose last digit is zero, then the number I divisible by 10.
Example: The numbers: 30, 50, 8000, 20 33000 are divisible by 10.
➤ Divisibility Rules for 11
This rule states that a number is divisible by 11 if the difference of the sum of alternative digits is divisible by 11.
 Divisibility Rule of 11
Divisibility Rule of 11
Example: To check whether number 2143 is divisible by 11 or not.
The sum of alternative digits of each group: 2 + 4 = 6 and 1+ 3 = 4
Since 6 - 4 = 2, Therefore 2143 is not divisible by 11.
➤ Divisibility Rules for 12
If the number is divisible by both 3 and 4, then the number is divisible by 12 exactly.
 Divisibility Rule of 12
Divisibility Rule of 12
➤ Divisibility Rules for 13
To check whether a number is divisible by 13, repeated addition of the last digit is done 4 times to the remaining number until a two-digit number is arrived at.
If the two-digit number is divisible by 13, then the whole number is also divisible by 13.
 Divisibility Rule of 13
Divisibility Rule of 13
Example: 2795 → 279 + (5 x 4) → 279 + (20) → 299 → 29 + (9 x 4) → 29 + 36 →65.
Since the two-digit number is found to be 65, which is divisible by 13.
Therefore, the number 2795 is also divisible by 13.
Solved Questions: Factors
Example 1: How many factors of the number 28 x 36 x 54 x 105 are multiples of 120?
a. 540
b. 660
c. 594
d. 792
Ans: Option 'c'
Sol: The prime factorization of 28 x 36 x 54 x 105 is 213 x 36 x 59.
Now, 120 can be prime-factorized as 23 x 3 x 5.
All factors of 213 x 36 x 59 that can be written as multiples of 120 will be of the form 23 x 3 x 5 x K.
213 x 36 x59 = 23 x 3 x 5 x K
=> K = 210x 35 x58.
The number of factors of N that are multiples of 120 is identical to the number of factors of K.
Number of factors of K = (10 + 1) (5 + 1) * (8 + 1) = 11 x 6 x 9 = 594
Example 2: Number N = 26 x 55 x 76 x 107; how many factors of N are even numbers?
a.1183
b. 1200
c. 1050
d. 540
Ans: Option 'a'
Sol: The prime factorization of 26 x 55 x 76 x 107 is 213 x 512 x 76.
The total number of factors of N = 14 x 13 x 7
We need to find the total number of even factors. For this, let us find the total number of odd factors and then subtract this from the total number of factors. Any odd factor will have to be a combination of powers of only 5 and 7.
Total number of odd factors of 213 x 512 x 76 = (12 + 1) x (6 + 1) = 13 x 7
Total number of factors = (13 + 1) x (12 + 1) x (6 + 1)
Total number of even factors = 14 x 13 x 7 - 13 x 7
Number of even factors = 13 x 13 x 7 = 1183
Example 3: If a three digit number ‘abc’ has 3 factors, how many factors does the 6-digit number ‘abcabc’ have?
a. 16 factors
b. 24 factors
c. 16 or 24 factors
d. 20 factors
Ans: Option 'c is correct
Sol: ‘abc’ has exactly 3 factors,
so ‘abc’ should be square of a prime number. (Important ot remember)
Any number of the form paqbrc will have (a + 1) (b + 1) (c + 1) factors, where p, q, r are prime.
So, if a number has 3 factors, its prime factorization has to be p2.
‘abcabc’ = ‘abc’ * 1001 or abc * 7 * 11 * 13
Now, ‘abc’ has to be square of a prime number.
It can be either 121 or 169 (square of either 11 or 13) or it can be the square of some other prime number.
When abc = 121 or 169, then
‘abcabc’ is of the form p3q1r1 1, which should have 4 * 2 * 2 = 16 factors.
When ‘abc’ = square of any other prime number (say 172 which is 289) ,
then ‘abcabc’ is of the form p1q1r1s2 , which should have 2 * 2 * 2 * 3 = 24 factors
So, ‘abcabc’ will have either 16 factors or 24 factors.
Example 4: A number N2 has 15 factors. How many factors can N have?
a. 5 or 7 factors
b. 6 or 8 factors
c. 4 or 6 factors
d. 9 or 8 factors
Ans: Option 'b' is correct.
Sol: Any number of the form paqbrc will have (a + 1) (b + 1) (c + 1) factors, where p, q, r are prime. (This is a very important idea)
N2 has 15 factors.
Now, 15 can be written as 1 x 15 or 3 x 5.
If we take the underlying prime factorization of N2 to be paqb,
then it should have (a + 1) (b + 1) factors.
So, N can be of the form
p14 or p2q4
p14 will have (14 + 1) = 15 factors
p2q4 will have (2 + 1) x (4 + 1) = 15 factors.
Importantly, these are the only two possible prime factorizations that can result in a number having 15 factors.
Hence the answer is 6 or 8 factors.
|
171 videos|161 docs|118 tests
|
FAQs on Important Formula: Remainder & Divisibility - Quantitative Aptitude (Quant) - Interview Preparation
| 1. What are the basic theorems of divisibility? |  |
| 2. How can I find the prime factorization of a number? |  |
| 3. What are some common divisibility rules? |  |
| 4. Can you explain how to solve questions based on factors? |  |
| 5. Why is understanding factors and divisibility important for exams? |  |
















