Chapter 11 - Electrostatics - JEE PDF Download

Charge

• Quantization: Charge is always in the form of an integral multiple of electronic charge and never its fraction.
  q = ±ne where n is an integer and e = 1.6 x 10^-19 coulomb
  = 1.6 x 10^-19 C.
  Charge on an electron/proton is the minimum charge.
• Particles, known as quarks, are predicted theoretically by charges Gell-mann. Quarks contain
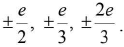
  Nobel prize of physics declared in 2004 refers to quarks.
• Millikan's oil drop experiment showed the discrete nature of charge. Charge cannot be fractional multiple of e. Quarks now throw a challenge.
• Charge on an electron is -ve. e = -1.6 x 10^-19 C.
  Charge on a proton is +ve. e = +1.6 x 10^-19 C.
  Total charge = ± ne.
• A particle/body is positively charged because it loses electrons or it has shortage of electrons.
• A particle is negatively charged because it gains electrons or it has excess of electron.
• Conservation: The total net charge of an isolated physical system always remains constant. Charge can neither be created nor destroyed. It can be transferred from one body to another.

Coulomb's inverse square law

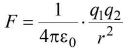• where F denotes the force between two charges q₁ and q₂ separated by a distance r in free space. ε₀ is a constant known as permittivity of free space. Free space is vacuum and may be deemed to be air practically.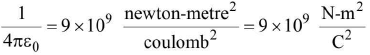
• 
• If free space is replaced by a medium, then ε₀ is replaced by (ε₀) or (ε₀ε_r) where K is known as dielectric constant or relative permittivity or specific inductive capacity (S.I.C.) or dielectric coefficient of the medium/material/matter. Thus
  
• 
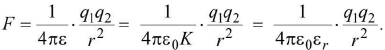
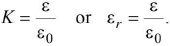
• K = 1 for vacuum (or air), K = ∞ for conductor/metal. 
• ε₀ = 8.85 x 10^-12 C² N^-1 m^-2.
• Vector form of the law (q₁ and q₂ are like charges)
  (i)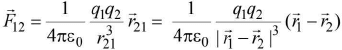 
  (ii)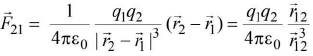
• If 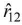 is a unit vector pointing from q₁ to q₂, then
  (i)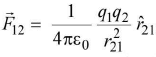 = force on q₁ by q₂.
  When q₁q₂ > 0 for like charges.
  (ii)  = force on q₂ by q₁
• When q₁q₂ > 0 for like charges .

Intensity/strength of electric field

• Intensity at a point is numerically equal to the force acting on a unit positive charge placed at the point.
• It is a vector quantity.
• The units of intensity E are NC^-1, volt/metre.
• The dimensions of E are [MLT^-3TA^-1].
• Intensity due to a charge q at distance r
  (i)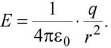
  It acts in the direction in which a +ve charge moves.
  (ii)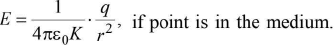
• Potential (V) and intensity (E)
  (i)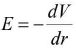 when potential varies with respect to distance. 
  (ii) when potential difference is constant.
  (iii) Potential at a point distance r from charge q.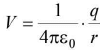
   in free space
  (iv)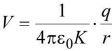in medium
  (v) Potential is a scalar quantity
  
• From positively charged surface, 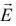 acts outwards at right angles i.e. along outward drawn normal.
• Intensity is equal to flux (number of electric lines of force) crossing unit normal area.
  

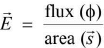
Electric lines of force

• Electric lines of force start from positive charge and terminate on negative charge.
• From a positively charged conducting surface lines of force are normal to surface in outward direction.
• Electric lines of force about a negative point charge are radial, inwards and about a positive point charge are radial, outwards.
• Electric lines of force are always perpendicular to an equipotential surface.
• These lines of force contract along the length but expand at right angles to their length. There is longitudinal tension and lateral pressure in a line of force. Contraction shows attraction between opposite charges while expansion indicates that similar charges repel.
• The number of electric lines of force (flux) passing through unit normal area at any point indicate electric intensity at that point.
• For a charged sphere these lines are straight and directed along radius.
• These may be open or closed curves. They are not necessarily closed though the magnetic lines of force are closed.
• Two lines of force never intersect or cut each other.
• Lines of force are parallel and equally spaced in a uniform field.
• Tangent to the curve at a point shows direction of field.

Gauss law

• For a closed surface enclosing a net charge q, the net electric flux ϕ emerging out is given by
  
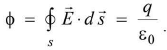
• If a dipole is enclosed by a closed surface, flux ϕ is equal to zero.
  Here the algebraic sum of charges (+q - q = 0) is zero.
• The flux will come out if +ve charge is enclosed. The flux will enter if negative charge is enclosed.
• Flux from a cube
  (i) If q is at the centre of cube, total flux (ϕ) = q/ε₀.
  (ii) From each face of cube, flux = q/6ε_0.
• Electric field due to a charged shell
  (i) At an external point, E =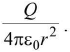
  This is the same as the field due to a point charge placed at the centre.
  (ii) At a point on surface of shell, this is E_max.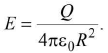
  
  Again the shell behaves like a point charge placed at the centre.
  (iii) At an inside point (r' < R), E = 0.
  Thus a charge q placed inside a charged shell does not experience any force due to the shell.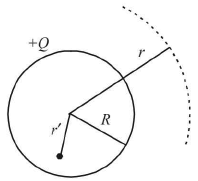
  
  Gaussian surface
  (i) For a sphere or spherical shell - a concentric sphere.
  (ii) For a cylinder or an infinite rod - a coaxial cylinder.
  (iii) For a plate - a cube or a cuboid.

Potential and intensity due to a charged conducting sphere (or shell)

• At a point outside the charged sphere
  (i) Intensity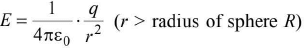  
  It is a vector quantity.
  (ii) Potential V =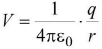 It is a scalar quantity.
• At a point on the surface of charged sphere
  (i) Intensity  
  Intensity is a vector quantity.
  (ii) Potential V =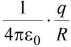 Potential is a scalar quantity.
• At a point inside the sphere (r < radius of sphere)
  (i) Intensity E = zero.
  (ii) Potential V =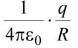
  Potantial is constant inside the sphere. This is same as potential at the surface of sphere.
• At the centre of sphere
  (i) Intensity E = zero.
  (ii) Potential V =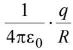
• At infinity
  (i) Intensity E = zero.
  (ii) Potential V = zero.

Electric field and potential due to charged non-conducting sphere

• Outside the sphere when r > radius of sphere R
  (i) Electric intensity E =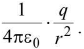 It is a vector quantity.
  (ii) Electric potential V =  It is a scalar quantity.
• On the surface of the sphere where r = R
  (i) Electric intensity E =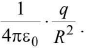 Intensity is a vector quantity.
  (ii) Electric potential V =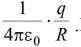 Potential is a scalar quantity.
• Inside the sphere when r < R
  (i) Electric intensity E =
  (ii) Electric potential V =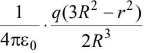
• At the centre of sphere when r = 0
  (i) Electric intensity E = zero.
  (ii) Electric potential V =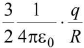
  ∴ Potential at centre =
• At infinity
  (i) Intensity = zero.
  (ii) Potential = zero.
  Electric dipole
• Two equal and opposite charges (q) each, separated by a small distance (l) constitute an electric dipole. Many of the atoms/molecules are dipoles.
  (i) Dipole moment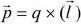
  (ii) Dipole moment is a vector quantity.
  (iii) The direction of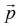  is from negative charge to positive charge.
  (iv) Unit of dipole moment = coulomb-metre = Cm.
  (v) Dimension of dipole moment = [ATL].
• Intensity of electric field due to a dipole
  (i) Along axis at distance r from centre of dipole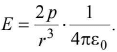
  
  Direction of E is along the direction of dipole moment.
  (ii) Along equator of dipole at distance r from centre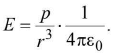
  Direction of E is antiparallel to direction of p.
  (iii) At any point along direction θ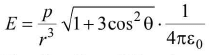
  
  The direction of E makes an angle β with the line joining the point with centre of dipole where tanβ =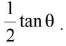
• Torque on a dipole
  
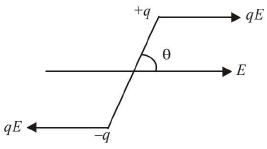
• Two forces [qE and (-qE)] equal, opposite and parallel, separated by a distance constitute a couple.
  
• This direction of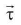is perpendicular to the plane containing  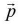and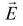. The torque tends to align the dipole in the direction of field.
• When dipole is parallel to electric field, it is in stable equilibrium. When it is antiparallel to electric field, it is in unstable equilibrium.
• Torque is maximum when θ = 90°. Dipole is perpendicular to E. Therefore maximum torque = pE.

Potential energy of dipole in uniform electric field

• Workdone in rotating the dipole from an angle 0 t to angle 0 2.
  

  

  
  

  

  
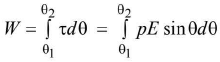
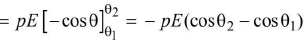
  (i) If θ₁ = 0 and θ₂ = 180°, W= 2pE.
  (ii) if θ₁ = 0 and θ₂ = 90°, W = pE.
• Potential energy of dipole, when it is turned through an angle 0 from field direction is
  
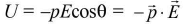
  (i) If θ = 0, U= -pE.
  The dipole orients itself parallel to field.
  (ii) If θ = 90°, U= 0.
  (iii) If θ = 180°, U = pE.
• Variation of potential energy of dipole with angle θ, between  and 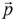 , is shown in the figure.(i) Potential energy is negative from 0 to π/2 and 3n/2 to 2π. They are regions of stable equilibrium of dipole.
  (ii) Potential energy is positive from π/2 to 3π/2. This is the region of unstable equilibrium of the dipole.
  

Dipole in non-uniform electric field

• In non-uniform electric field, the two ends of dipole are acted upon by forces qE₁ and -qE₂. They are not equal as E₁ ≠ E₂ in non-uniform field. Hence a force and a torque both act on the dipole.
• Force acting on the dipole can be represented by
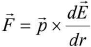
• Broadly speaking,Net force = (qE₁ - qE₂) along direction of greater field intensity.
• On account of net force upon dipole, it may undergo linear motion.
• In a non-uniform electric field, a dipole may, therefore, undergo rotation as well as linear motion.

Potential energy of charge system

• For two point charges q₁ and q₂ separated by a distance r, electrostatic potential energy U is given by
  
  
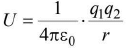
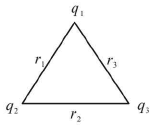
• For three point charges, U =
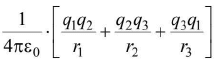
• For n charges, consider all pairs with due regard of signs of charges, positive or negative.
• S I. unit of energy = joule (J)
• Another popular unit is electron volt (eV).
• 1 eV = 1.6 x 10^-19 joule.

Charged soap bubble

For equilibrium of a charged soap bubble, pressure due to surface tension = 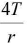 acting inwards.
Electric pressure due to charging 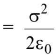acting outwards.
At equilibrium, 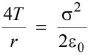where σ = surface density of charge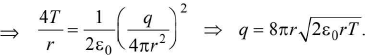

Here air pressures, inside and outside the bubble, are supposed to be same.

Behaviour of a conductor in an electrostatic field

In the case of a charged conductor
(i) charge resides only on the outer surface of conductor.
(ii) electric field at any point inside the conductor is zero.
(iii) electric potential at any point inside the conductor is constant and equal to potential on the surface of the conductor, whatever be the shape and size of the conductor.
(iv) Electric field at any point on the surface of charged conductor is directly proportional to the surface density of charge at that point, but electric potential does not depend upon the surface density of charge.

Capacitance

• When a conductor is given a charge, its potential gets raised. The quantity of charge given to a conductor is found to be directly proportional to the potential raised by it. If q is the charge given to conductor and V is potential raised due to it, then q ∝ V or q = CV, where C is a constant, known as capacitance of the conductor.
• Capacitance = charge/potential.
• Unit of capacitance is farad.
  IF = 1 coulomb/volt.
• 1 Farad = 9x 10¹¹ stat farad.
• Dimensions of capacitance are [M^-1 L^-2 T⁴ A²].
• Capacity of an isolated spherical conductor : Capacitance of an isolated spherical conductor of radius a placed in a medium of dielectric constant K,
  C = 4πε₀Ka farad
  For vaccum or air, K = 1, hence
  C0 = 4πε₀a farad.
  i.e., capacitance of a spherical conductor ∝ radius.
• Capacitor is a pair of two conductors of any shape which are close to each other and have equal and opposite charges.
• A capacitor is an arrangement which can store sufficient quantity of charge.
• The quantity of charge that can be given to a capacitor is limited by the fact that every dielectric medium becomes conducting at a certain value of electric field.
• Capacitance of a capacitor is
  (i) Directly proportional to the area of the plates (A).
  (ii) Inversely proportional to distance between plates (d)^-1.
  (iii) Directly proportional to dielectic constant of the medium filled between its plates (K).
• Parallel plate capacitor : Capacitance of a parallel plate capacitor filled completely with some dielectric medium.
  
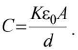
• For air and vacuum, K = 1.
  
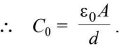
• Capacitance of a parallel plate capacitor filled with dielectric slab of thickness t is given by
  
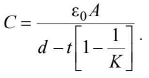
• Capacitance of a parallel plate capacitor filled with a conducting slab of thickness t is given by
  
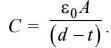
• The plates of a parallel plate capacitor attract each other with a force F =
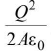
• Capacitance of a spherical condenser/capacitor, is
  C = 4πε₀K [ab/(b - a)]
  when a and b are the radii of inner and outer spheres respectively.
• Dielectrics are of two types : Non-polar and polar. The non-polar dielectrics (like N₂, O₂, benzene, methane) etc. are made up o f non-polar atoms / molecules, in which the centre of mass of negative coincides with the centre of mass of negative charge of the atom / molecule.
• The polar dielectrics (like H₂O , CO₂, NH₃, HC1) etc. are made up o f polar atoms / molecules, in which the centre of mass of positive charge does not coincide with the centre of mass of negative charge of the atom / molecule.
• A non-polar dielectric can be polarized by applying an external electric field on the dielectric.
• The effective electric field £ in a polarised dielectric is given by 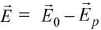where 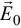 is strength of external field applied and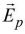is intensity of induced electric field set up due to polarization. It is equal to surface density of induced charge. The ratio E₀ / E = K, dielectric constant.
• When a dielectric slab is placed between the plates of a parallel plate capacitor, the charge induced on its sides due to polarization of dielectric is
  
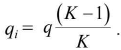
• Capacitors in series: Equivalent capacitance of a series combination of capacitors is
  
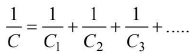
• In series combination of capacitors, charge is same on each capacitor and is equal to charge supplied by source CV= C₁V₁ = C₂V₂ = ...
• Capacitors in parallel: Equivalent capacitance of a parallel combination of capacitors is C_p = C₁ + C₂ + C₃ +....
• In parallel combination of capacitors, potential difference is same across each capacitor and is equal to applied potential difference
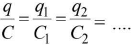
• Electric potential energy stored in a charged conductor or capacitor is
  
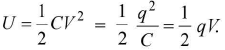
• The electric potential energy of capacitor resides in the dielectric medium between the plates of the condenser.
• When two charged conductors are connected together, the redistributed charges on them are in the ratio of their capacitance.
• When two charged conductors having charges q₁ and q₂ and capacitances C₁ and C₂ are connected together, then after redistribution of charges, the common potential is
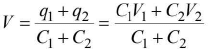  where V₁ and V₂ are the initial potentials of the charged conductors.
• In case of charged capacitors, when plates of same polarity are connected together, common potential
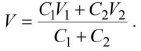
  But when plates of opposite polarity are connected together, then common potential is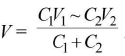
  
• Total energy stored in any grouping of capacitors is equal to sum of the energies stored in individual capacitors.
• If n charged drops, each of capacity C, charged to potential V with charge q, surface density σ and potential energy U coalesce to form a single drop, then for such a drop, total charge = nq
  total capacity = n^1/3 C
  potential = n^2/3V
  Surface density of charge = n^1/3σ,
  and total potential energy = n^2/3U.
• Sharing of charges
  (i) Common potential : When two capacitors at different potentials V₁ and V₂ are connected, charged q₁ (= C₁V₁) and q₂ (= C₂V₂) are redistributed till a common potential V is reached. Then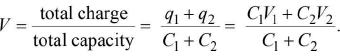
  
  (ii) Loss of energy : During sharing o f charges, energy is lost; mostly as heat, partly as cracking noise and partly as sparking light.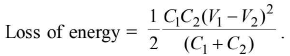
  

Van de Graaff generator

• Van de Graaff designed this electrostatic machine in 1931 to build up high potential difference of the order of few million volt.
• The generator is based on the following points:
  (i) The action of sharp points i.e. the phenomenon of corona dischage.
  (ii) The property that the charge resides on the outer surface of a conductor. Charge given to a hollow conductor is transferred to outer surface and is distributed uniformly over it.
• The high potential generated is used to accelerate charged particles like electrons, protons, ions etc. The particles hit the target with the huge energy acquired and carry out the artificial transmutation etc.
• ∵ Capacity of a spherical shell = 4πε₀R
  ∴
  or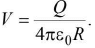
  
  The positive charge goes on accumulating on the large spherical conducting shell.
  ∴ Energy of the ions to be accelerated = qV where q denotes charge on the ion or particle accelerated to hit the required target.