Chapter - 1 Units and measurement - JEE PDF Download

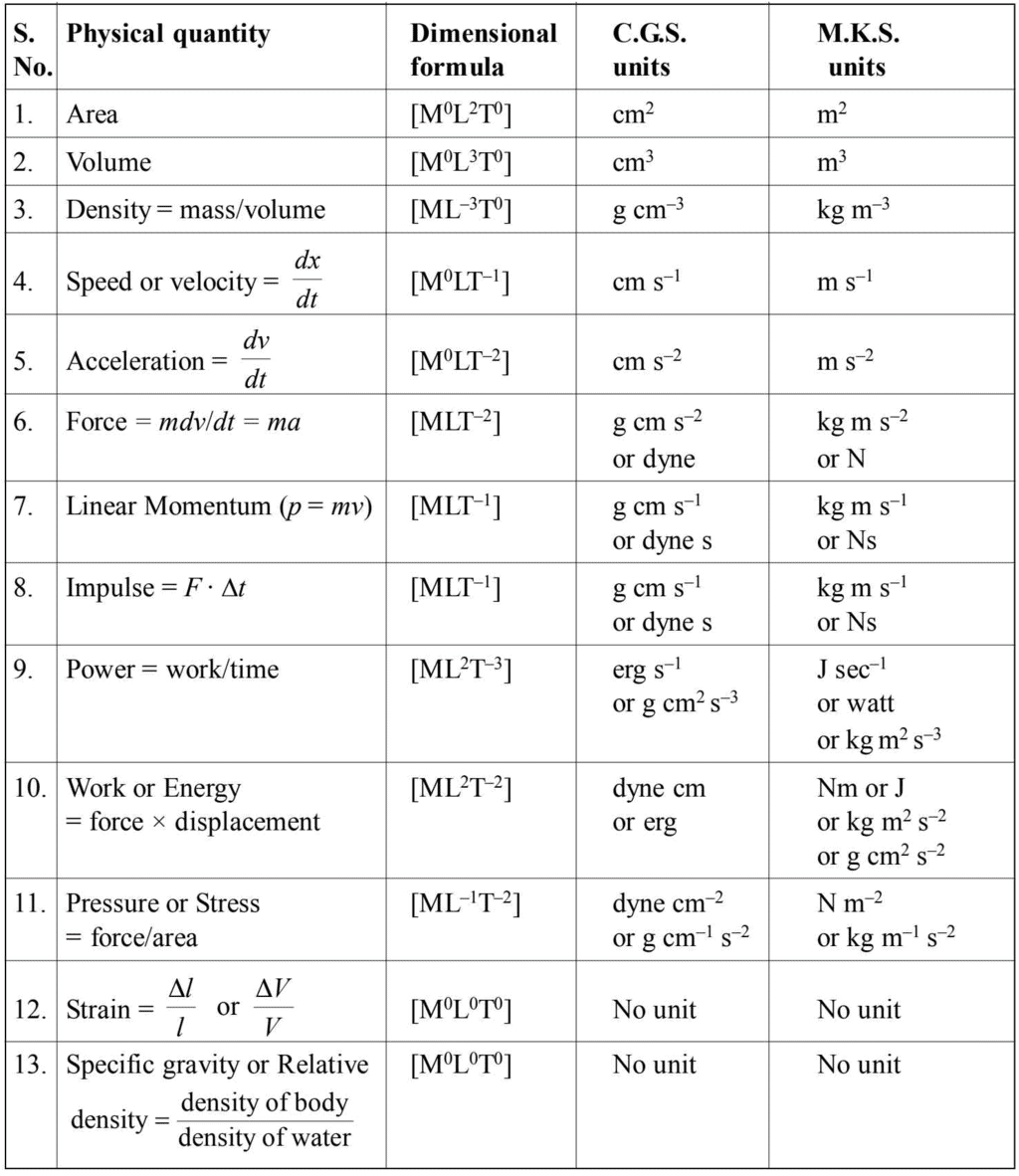
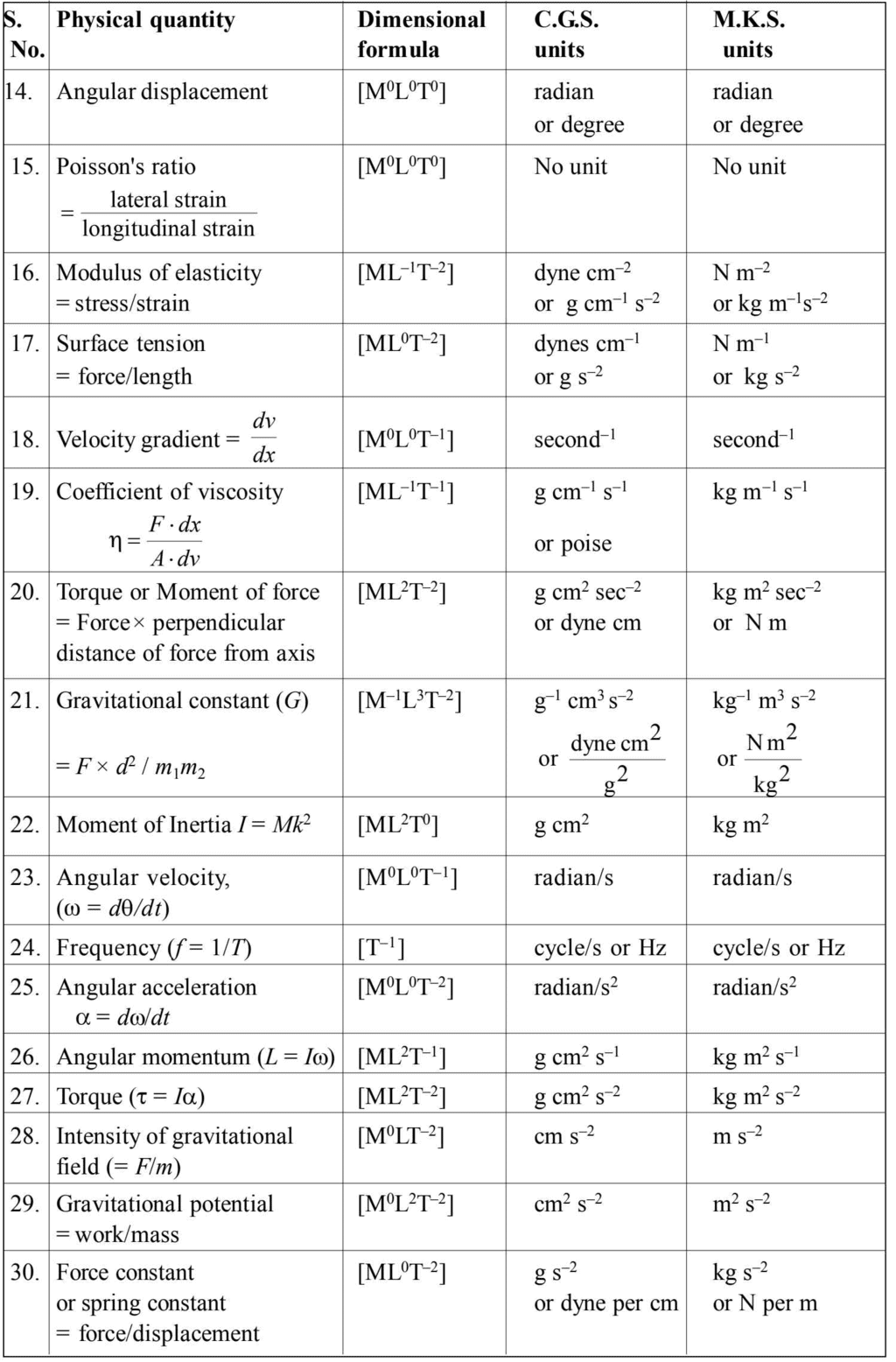
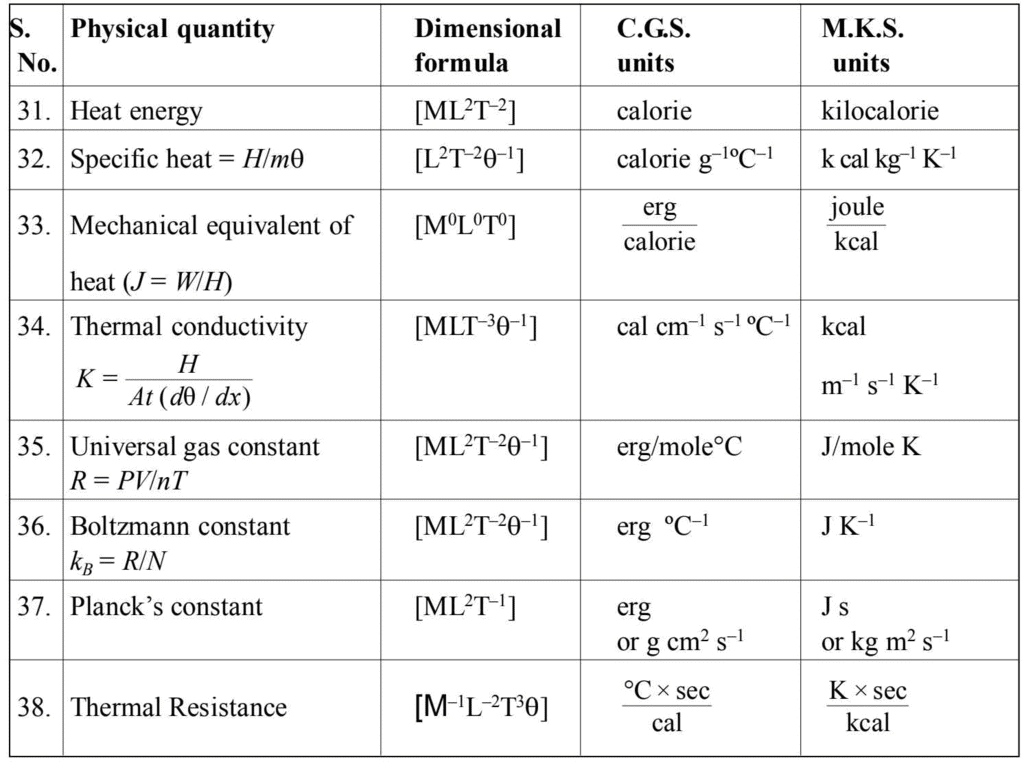
• Units and dimensional formulae of some important physical quantities.

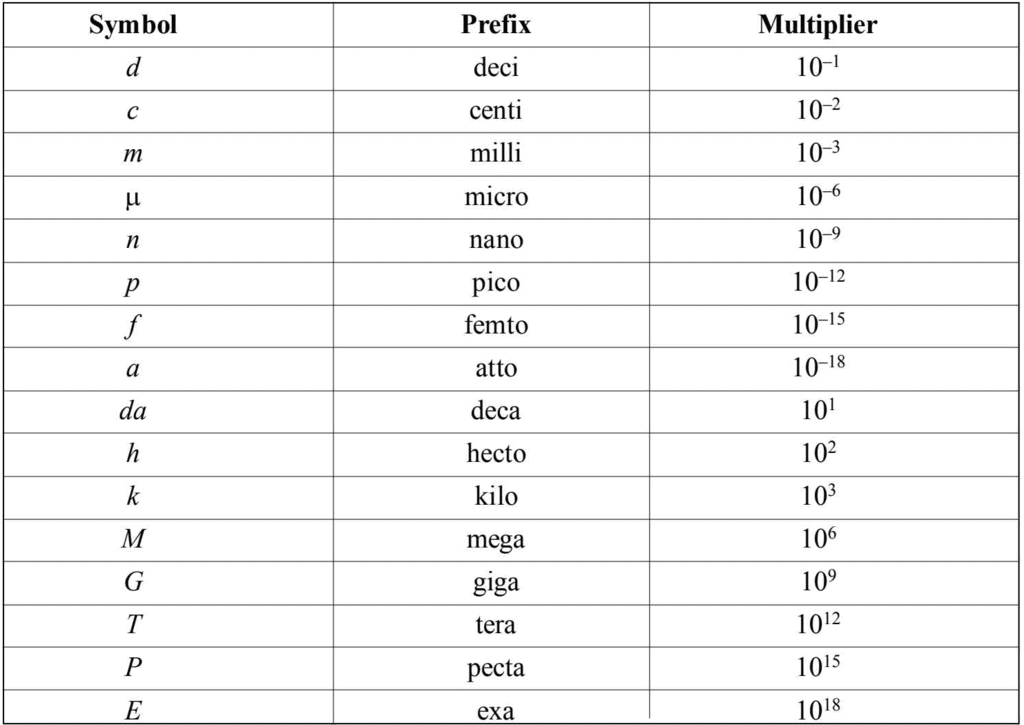
• Some important abbreviations

Significant Figure Rule

• So far significant figures are concerned, in mathematical operations like addition and subtraction, the result would be correct up to minimum number of decimal places in any of quantities involved. However, in multiplication and division, number of significant figures in the result will be limited corresponding to the minimum number of significant figures in any of the quantities involved.
• To represent the result to a correct number of significant figures, we round off as per the rules.
• There are three rules on determining how many significant figures are in a number :
  (i) Non-zero digits are always significant.
  (ii) Any zeros between two significant digits are significant.
  (iii) A final zero or trailing zeros in the decimal portion ONLY are significant.
• All numbers are based upon measurements (except for a very few that are defined). Since all measurements are uncertain, we must only use those numbers that are meaningful. 
• A common ruler cannot measure something to be 22.4072643 cm long. Not all of the digits have meaning (significance) and, therefore, should not be written down. In science, only the numbers that have significance (derived from measurment) are written.
• Rule 1: Non-zero digits are always significant. Number like 26.38 would have four significant figures and 7.94 would have three. The problem comes with numbers like 0.00980 or 28.09.
• Rule 2: Any zeros between two significant digits are significant, e.g. 406 have 3 significant figures.
• Rule 3: A final zero or trailing zeros in the decimal portion only are significant. e.g. 0.00500 m only three number are significant.The zero at left of non-zero and after decimal point are not significant figures. Another way the number 0.00500 m can be written in scientific notation (in power of 10) is
  0.00500 m = 5.00 x l0^-3 m = 5.00 x 10^-1cm
  = 5.00 x 10^-6 km.The power 10 is not considered or irrelevant in significant figures.
• Rule 4: Trailing zeros in a whole number are not significant. e.g. 25,000 has two significant figures.
• Example
  0.009 g → has one significant figure and can be written as 9 x 10^-3 g.
  6.032 Nm^-2 → has four significant figures.
  0.000507 m2^-4 has three significant figures.
• When some value is recorded on the basis of some actual measurement, the zeros on the right of last non-zero digit become significant. For example, m = 100 kg has three significant figures.

Rounding Off

• Rule 1: If the digit to be dropped is less than 5, then the preceding digit is left unchanged. e.g. 8.22 is rounded off to 8.2.
• Rule 2: If the digit to be dropped is more than 5, then the preceding digit is raised by one. e.g. x = 6.87 is rounded off to 6.9.
• Rule 3: If the digit to be dropped is 5 followed by digit other than zero, then the preceeding digit is raised by one. e.g. 7.851 is rounded off to 7.9.
• Rule 4: If the digit to be dropped is 5 or 5 followed by zero, then preceding digit is left unchanged, if it is even. e.g. 5.250 rounding off to 5.2.
• Rule 5: If the digit to be dropped is 5 or 5 followed by zeros, then the preceding digit is raised by one, if it is odd. e.g. 3.750 is rounded off to 3.8.
• Accuracy is the extent to which a reported measurement approaches the true value of the quantity measured.

Absolute Error

• This error in the measurement of a quantity is the magnitude of the difference between the true value and the measured value of the quantity.
  Let in some experiment on physical quantity is measured n times. Let the measured values be a₁ a₂, .... a_n. The arithmetic mean of these value is

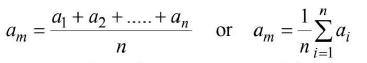
a_m is considered as true value of the quantity, if the true value of that quantity is not known.

• The absolute error in the measured values of quantity are
  Δa₁= a_m - a₁
  Δa₂ = a_m - a₂
  .........................
  ........................
  .........................
  .........................
  Δa_{n =am - an}
• The absolute error may be positive in certain cases and negative in certain other cases.

  Mean absolute Error
  It is the arithmetic mean of the magnitude of absolute errors in all the measurements of the quantity.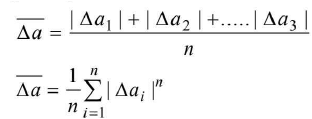
  

Hence the final result of measurement may be written as
 

Relative Error or Fractional Error

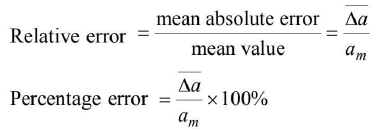
Propagation Or Combination Of Errors

• Error in sum of quantities
  Let x = a + b
  Let Δ a = absolute error in measurement of a
  Let Δ b = absolute error in measurement of b
  The maximum absolute error in x is
  Δx = ± (Δa + Δb)
• Error in difference of quantities
  Let x = a - b
  The maximum absolute error in x is Δx = ± (Δa + Δb)
• Error in product of quantities 
  x = a x b
  Maximum possible value of (or maximum fractional error or relative error in product)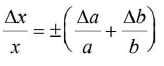
  
• Error in quantity raised to some power
  Let x=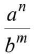 
  
• The fraction error or relative error.
  
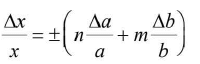
• • The initial and final temperatures of water as recorded by an observer are (40.6 ± 0.2)°C and (78.3 ± 0.3)°C. The rise in temperature with proper error limit is given by : Rise in temperature = 0 = 0₂ - 0₁ = 78.3 - 40.6 = 37.7°C Δ0 = (Δ0J + Δ02) = ± (0.2 + 0.3) = ±0.5°C.
• Hence rise in temperature = (37.7 ± 0.5)°C.
• Any order of magnitude is an exponential change of plus-or-minus 1 in the value of a quantity or unit. The term is generally used in conjunction with power-of-10 scientific notation.
• In base 10, the most common numeration scheme worldwide, an increase of one order of magnitude is the same as multiplying a quantity by 10. An increase of two orders of magnitude is the equivalent of multiplying by 100 or 10². In general, an increase of n orders of magnitude is the equivalent of multiplying a quantity of 10². This, 2315 is one order of magnitude larger than 231.5, which in turn is one order of magnitude larger than 23.15.
• For smaller value, a decrease of one order of magnitude is the same as multiplying a quantity by 0.1. A decrease of two orders of magnitude is the equivalent of multiplying by 0.01 or 10^-2. In general, a decrease of n orders of magnitude is equivalent of multiplying a quantity by 10^-n.
• In the Standard International (SI) System of Units, most quantities can be expressed in multiple or fractional terms according to the order of magnitude. For example attaching the prefix “kilo” to a unit increases the size of the unit by three orders of magnitude, or one thousand (10³).
  Attaching the prefix “micro” to a unit decreases the size of the unit by six orders of magnitude, the equivalent of multiplying it by one millionth (10^-6). Scientists and engineers have designated prefix multipliers from septillionths (10^-24) to septillions (10²⁴), a span of 48 orders of magnitude.

Trigonometric Identities 

• Reciprocal Identities
  
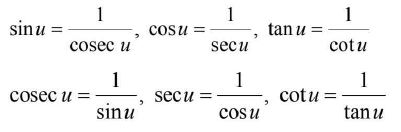
• Pythagorean identities
  sin² u + cos² u = 1
  1 + tan² u = sec² u
  1 + cot²u = cosec²u
• Quotient identities
  
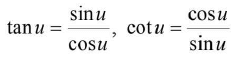
• Co-function identities
  
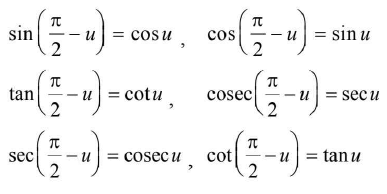
• Even-odd identities
  
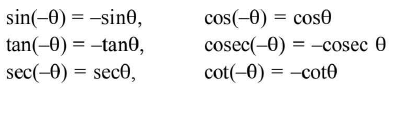
• Sum-difference formulae

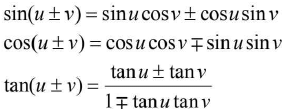
• Double angle formulae
  sin(2u) = 2 sin u cosu
  cos(2u ) = cos² u - sin² u = 2 cos² u - 1 = 1 - 2 sin² u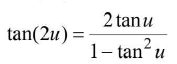
  
• Sum-to-product formulae
  
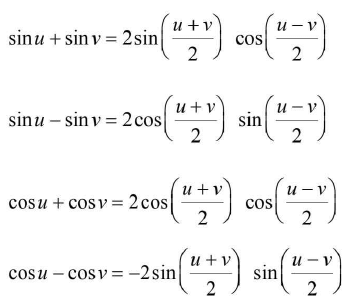
• Product-to-sum formulae
  

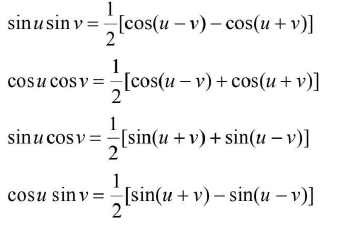
Measurement

• The mass, length and time in the physical world have variations from atomic to astronomical range. Measurements are an integral part of all advancements in modem science and technology. Extent of uncertainty is simultaneously taken in to account while reporting the results of research and exploration .

Measurement Of Length 

• The Indian national standards of seven base units are maintained at National Physical Laboratory (NPL), New Delhi.
• The standard of length (metre) is realised by employing a stabilised helium-neon laser as a source of light.
• Very small distances such as inter-molecular distances, size of molecules, radius of atom can be measured by electron microscope. Modern science has developed tunneling microscopes to resolve microscopic distances. Rutherford developed scattering method to measure distance of closest approach which is of the order of 10^-14 m.
• Very large distances such as the distance of a star from earth can be measured with the help of angular measurements or parallax methods. Sextant can measure height of mountains. Radar signal echo method or optical Doppler shift method provide measurements of diameters of moon and star.
• The following table displays the large variation in terms of order of magnitude of length.

Measurement of Mass

• The Indian national standard of mass is a copy No. 57 of the International prototype kilogram supplied by the International Bureau of Weights and Measures (BIPM).
• Science differentiates between the inertial mass and the gravitational mass.
• Inertial mass (m) = force/acceleration. It can be measured with the help of inertia balance.
• Gravitational mass of a body determines the gravitational pull due to earth acting upon the body. It can be measured with the help of a common balance. In order to measure the weight of a body, a spring balance is used.

The following table displays the huge variation in terms of order of magnitude of mass:

Measurement of time

• The national standard of time interval, second as well as frequency, is maintained through four cesium atomic clocks mentioned at NPL.
• The standard maintained at NPL is linked to different users in a variety of ways. This process is known as dissemination. Time is disseminated through TV, radio, special telephone service for day-to-day requirements. For high level of accuracy there is a satellite-based time dissemination service which utilized the Indian Satellite INSAT.
• The following table displays the low to high range of variation of time.

Units

• In the System International, length(m), mass(kg), time(s), electric current(A), thermodynamic temperature(K), luminous intensity(cd) and quantity of matter(mol) are considered as fundamental quantities. In this system, plane angle and solid angle are considered as supplementary quantities.
• The quantities that are derived using the fundamental quantities are called derived quantities. For example speed, volume, acceleration, force, momentum, etc.
• The units, that are used to measure the fundamental quantities are known as fundamental units.
• The units, that are used to measure the derived quantities are known as derived units e.g. metre2, newton, cubic metre, erg, watt, etc.
• Some more quantities which are found to be fundamental in nature are added to the existing list of fundamental quantities. The system consisting of all fundamental quantities is known as “System International” and units are called SI units.
• Units should not be expressed in capital letters. They should be written as newton, joule, watt, etc.
• Units can be expressed in full or by approved symbols.
• Units must be expressed in singular form. Example: 11 metre, 26 newton, 6 joule, etc.
• Symbols of units : When a unit is named after a scientist, the symbol is a capital letter. For other units, the symbol is not a capital letter. Thus symbol for kelvin, the unit of temperature is K. Similarly J (joule), N (newton), W (watt), P (pascal), C (coulomb), A (ampere), F (faraday), H (henry), V (volt), Wb (weber), T (tesla), Gs (gilbert), Q (ohm), S (siemen) represent other units. Correct symbol for gram is g, for kilogram is kg, for metre is m.
• Single solidus: In a symbol, more than one solidus should not be used. Acceleration should not be expressed as m/s/s. It should be written as ms^-2 or m/s². The index form ms^-2 is, however, preferred.
• No full stop after symbol. Volume should be written as cc and not as c.c.
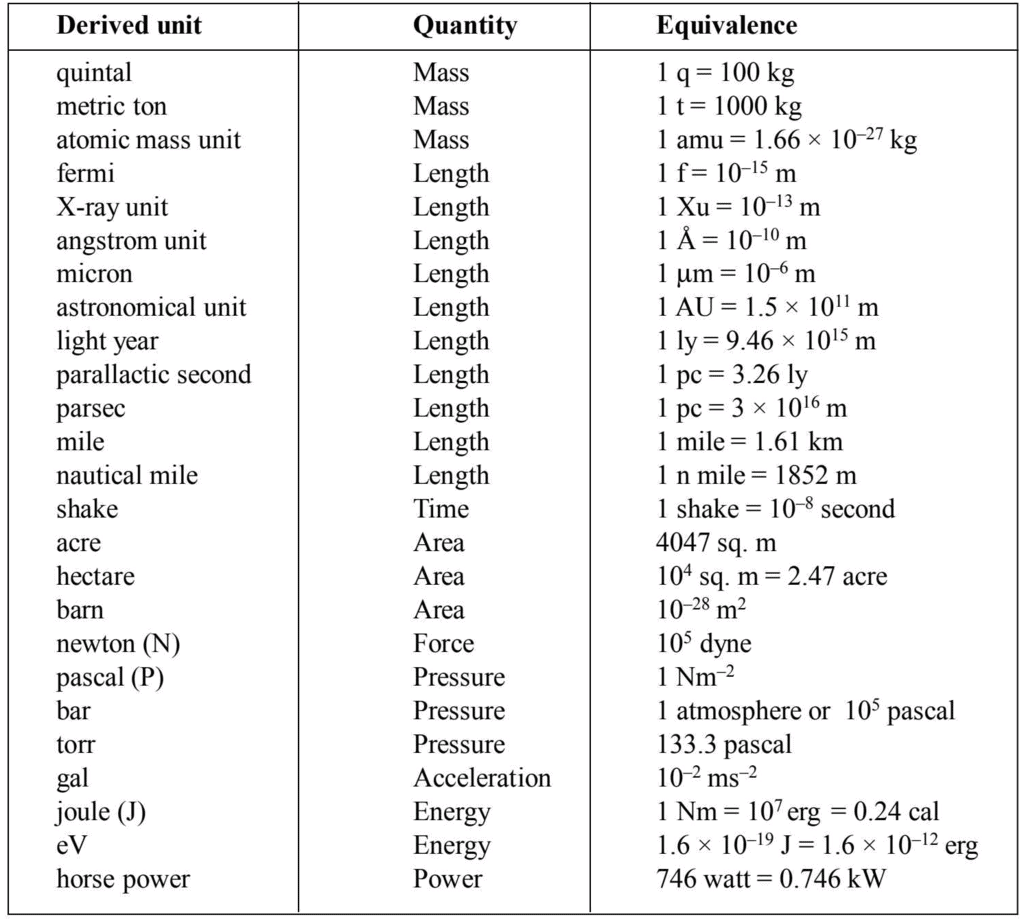
• Derived units and equivalences.

Dimensions

• The dimensions of a physical quantity are the powers to which the fundamental units are raised to obtain the unit of that quantity.
• Angle and ratio do not have dimensions.
• The dimensional equations are used
  (a) to verify whether an equation connecting physical quantities is correct or not.
  (b) to find the relation between systems of units of the same physical quantity.
  (c) to derive equations connecting physical quantities.
• The dimensional methods are applicable to equations connecting physical quantities alone.
• The dimensional methods are applicable to equations involving the three fundamental quantities only.
• The proportionality constants are to be found experimentally.
• How to obtain a dimensional formula? 
• (a) From the definition or from the defining equation:
  
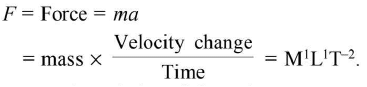
  (b) From a knowledge of the unit: 
  Planck’s constant = joule - sec = M¹L²T^-2T' = M¹L²PT^-l.
  (c) From a formula in which the required quantity appears:

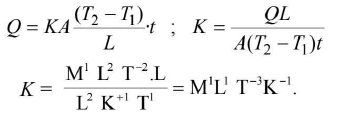
Important uses of dimensions illustrated 
(a) Conversion from one system to the other:

1 N = 10⁵ dyne.

(b) Investigating how the unit of a derived quantity change when the fundamental units L, M, T are altered.

Ex: If L, M and T are doubled, what happens to the unit of power.

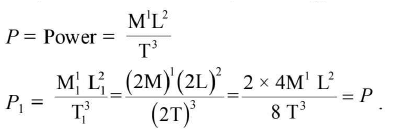
If L represents inductance, C represents capacitance, R represents resistance and q represents the charge, then
(i) L/R, RC, √LC have the dimensions o f time
(ii) R/L, \IRC1/√LC have dimensions of frequency.
(iii) q²/C, LI², qV, V²C, all have dimensions of energy.

If R is resistance, I is current, V is potential difference and t is time, then

(i) VI,  V²/R,I² R have the dimensions of power.

(ii) VI t, 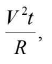I² Rt have the dimensions of energy.

• If m is mass, s is specific heat, Δ0 is change in temperature, L is latent heat, P is pressure, V is volume, T is temperature and R is gas constant, then ms Δ0 ; mL ; PV\ RT all have the same dimensions of energy [M¹L² T^-2].
• The principle of homogeneity of dimensions is used in checking the correctness of formulae, and also in the derivation of formulae.
• Only like quantities having the same dimensions can be added to or subtracted from each other.
• The order of accuracy obtained in adopting atomic standards of length and time, as detailed earlier is 1 part in 10⁹.
• Planck’s constant has the same dimensional formula as angular momentum, i.e. [M¹ L² T¹].
• Thermal capacity, Boltzmann constant, entropy have the same dimesions, i.e. [ML² T^-2 K^-1].
• Work, energy, kinetic energy, potential energy, couple, moment of a force, torque, internal energy, heat energy, electron volt, kilowatt, hour, etc. all have the same dimensional formula [M¹L² T^-2].
• The three coefficients of elasticity, stress, pressure have the same dimensions, i.e. [M ¹ L^-1 T ^-2].
• Strain, refractive index, relative density, angle, solid angle, trigonometrical ratios, phase, relative permittivity and relative permeability-all are dimensionless.
• Surface tension, surface energy, spring constant and force gradient have the same dimensional formula, i.e. [M¹L⁰T^-2].
• Force, thrust and weight have the same dimensional formula, i.e. [M¹L¹T^-2].
• Inertia and mass have the same dimensional formula.
• Relative velocity also has the dimensions of velocity.
• Distance travelled in nth second has the dimensions of velocity.