Chapter 18 - Ray Optics - JEE PDF Download

• Ray optics is based on the assumption that light travels along straight lines.
• Sources of light are of three types: thermal sources, gas discharge sources and luminescent sources.
• Photometry is a branch of ray optics which deals with the measurement of light energy.
• The amount of visible light energy emitted per second from the source is called luminous flux (Ф) of a source of light. The S.I. unit of luminous flux is lumen.
• The luminous flux emitted per unit solid angle in any direction is known as luminous intensity (I) of a light source. S.I. unit of luminous intensity is candle power or candela.
• Illuminance (E) of a surface is the luminous flux incident normally on unit area of the surface. Its unit is lux.
• Luminance or brightness (B) of a surface is the luminous flux reflected into our eyes from unit area of the surface. Its unit is lambert.
• According to Lambert’s cosine law, E ∝ cosθ, where θ is the angle which the incident light makes with normal to the surface at that point.
• A photometer is used for comparing the luminous intensities of two sources.
• Velocity of light, c =  and the most accurate value of c = 2.99797 x 10⁸ m/s.

Reflection of light

• Reflection of light is the phenomenon of change in the path of light without change in medium.
• Laws of reflection :
  (i) The incident ray, the reflected ray and the normal to the surface all lie in the same plane.
  (ii) The angle of incidence (i) is equal to the angle of reflection (r).
• Plane mirror : For image due to a plane mirror
  (i) Size of image = size of object Magnification = unity
  (ii) Distance of image (behind mirror) = distance of object
  (iii) Image is erect and virtual.
  (iv) There is a lateral invertion in the image.
  (v) A plane mirror may form a virtual as well as real image.
• Size of plane mirror = half the size of a person. A man of 6' height may see his full image in a mirror of 3' height.
• Number of images of a object
  When two plane mirrors are held at an angle 0, the number of images of an object placed between them is given as below.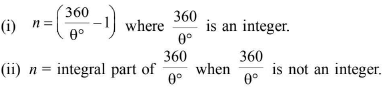
  
• A thick mirror forms a number of images, out of which second one is the brightest.
• Kaleidoscope and periscope employ the principle of image formation by plane mirrors.
• A plane mirror may form a real image, when the pencil of light incident on the mirror is convergent. Children, during their play, form an image of Sun on wall by a strip of plane mirror.
• Convex mirror : Image formed is always diminished, virtual, erect and behind the mirror.
• Focal length of mirror = 1/2 x radius of curvature of the mirror
  ⇒ f = R/2.
• Field of view is large as the image formed is diminished.
• 
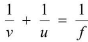
  Using the convention of signs of coordinate geometry, when light travels from left to right, u is - ve and v , f, R, magnificationare all +ve.
• When object is situated at pole of mirror, the image is also formed at the pole of the surface. The behaviour at pole is same as with a plane mirror.
• A convex mirror is used in street lights and by the side of driver of a car/scooter for seeing the back-view. The large field of view helps in movement of vehicle ahead.
• Concave mirror :
  
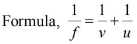
• R = 2f
• A concave mirror forms variety of real and virtual images.
• For all real images which are formed on the side o f object, v, u , f magnification, R and height of image are -ve. Height of object is +ve. Sign convention of coordinate geometry is followed. Object is situated to left of mirror. Incident rays travel from left to right.
• For virtual image v, S.I., S.O. and m are +ve while u , f R are -ve.
• Real image of same size is formed at the object itself only with a concave mirror. The object should be placed at centre of curvature. The real image is also formed at C.

  Magnification = -1.

• When object is placed at pole of concave (or convex) mirror, virtual image of same size is formed at the pole itself. It is, infact, a plane mirror behaviour for this position of object.

• A concave mirror is used in search lights, head lights and torches. It is also used as mirror for shaving and make-up purposes where in a virtual image, larger than the object is formed, to display details of the object.

• For concave mirror, f² = x₁,x₂ where x₁, and x₂ denote distances o f object and its image from focus of concave mirror. This is known as Newton's formula. The formula does not apply to convex mirror.

Refraction of light

• When a ray of light is incident on the boundary between two transparent media, a part of it passes into the second medium with a change in direction. This phenomenon is called refraction.
• Laws of refraction :
  (i) The incident ray, the refracted ray and the normal all lie in the same plane.
  (ii) Snell’s law : The ratio of the sine of the angle of incidence to the sine of angle of refraction is constant for two given media. This constant is called refractive index (μ) of medium 2 with respect to medium 1. i.e. μ = sini/sinr, where i is the angle of incidence and r is the angle of refraction.
• Refractive index (μ) - In short, R.I. (μ) : Refractive index o f a material depends upon four factors as follows:
  (i) Material: Refractive index is maximum for diamond. Its value is 2.42. It is rated to be one for vacuum or almost unity for air. This value of R.I. is minimum.
  Refractive index of carbon di sulphide liquid ≈ 1.6
  Refractive index of water = 4/3 = 1.33
  Refractive index of glass = 3/2=1.50
  Refractive index of glycerine ≈ 1.47 ≈ 1.50 ≈ R.I. of glass
  (ii) Colour of light
  - Refractive index of violet colour is maximum while that for red light is minimum. μ_{V >} μ_R.
  VIBGYOR denotes seven colours in descending order of R.I.
  Thus μ_V > μ_I > μ_B > μ_G > μ_Y > μ_O > μ_R.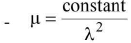
  generally. Specifically ,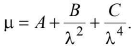This is Cauchy's formula.
  (iii) Temperature/density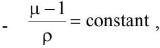
  where ρ denotes density of material. Since density decreases with rise of temperature, R.I. also decreases with rise of temperature
  - μ is inversely proportional to temperature,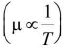
  (iv) Surrounding media
  - R.I. of medium y with respect to medium x is represented as ^xμ_y or μ_xy and here the ray of light travels from x to y.
  - If light travels from y to x, R.I. = ^yμ_x.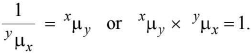
  
  - If glass is surrounded by water, R.I. = ^wμ_g.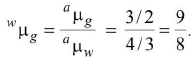
  
• R.I., speed of light, wavelength of light
  xμ_y = R.I. of y with respect to x.
  
• In a given transparent medium/material, velocity of light is not same for all colours. It is different for different colours/wavelengths λ/frequencies n. Red colour travels fastest and violet light travels slowest in a given transparent medium/material.
  v_R > v_O > v_Y > v_G > v_B > v_I > v_V
• In vacuum, all colours travel with the same speed. Velocity of light in vacuum is an absolute constant. Its value is, c = 3 x 10⁸ m/s. It does not depend upon colour (wavelength or frequency) of light, amplitude, intensity of light, velocity of source or velocity of observer.
• Quantities which remain constant during refraction are
  (i) frequency of light. Frequency depends upon source of light.
  (ii) Phase angle.
• Quantities which change during refraction are:
  (i) Speed of light. Denser the medium, less the velocity.
  (ii) Wavelength of light. Denser the medium, less the wavelength.
  (iii) Amplitude of light.
  (iv) Intensity of light. This is due to the partial reflection and partial absorption of light.
• The cause of refraction is that light travels faster in a rarer medium than in a denser medium.
  
  Frequency n does not change during refraction.
• ^aμ_m = R.I. of medium m with respect to a (or vacuum)
  
  Denser the medium (i.e. greater ^aμ_m), less the speed of light in it and less the wavelength of light in it (the medium).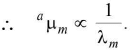
  
• Apparent depth - If an object is placed below the surface of water or under a glass slab, it appears to be raised, i.e. the apparent depth is less than the real depth. This is due to refraction. Refractive index (μ) can also be given as
  μ = real depth/apparent depth.
• Total internal reflection is the phenomenon of reflection of light into the denser medium from the boundary of the denser medium and rarer medium.
• The angle of incidence (i) in denser medium for which the angle of refraction in rarer medium is 90° is called the critical angle for the pair of media under consideration.
• Refractive index (R.I.) and critical angle
  Critical angle is the angle of incidence in denser medium for which angle of refraction in rarer medium is 90°.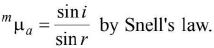
  
  Ray travels from the denser medium to air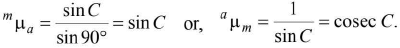
• Critical angle increases with temperature
• Denser the medium, less the critical angle.
• Regarding colour/wavelength or frequency o f light, μ_V > μ_R . Hence C_V< C_R.

  Critical angle for violet colour is lowest.

  Critical angle for red colour is highest.

• Critical angle for diamond = 24°
  Critical angle for glass = 42°
  Critical angle for water = 48°

• Total internal reflection occurs if angle of incidence in denser medium exceeds critical angle.

• Mirage is an optical illusion observed in deserts and roads on a hot day when the air near the ground is hotter and hence rarer than the air above.

• Optical fibres consist of long fine quality glass or quartz fibres, coated with a thin layer of a material of lower refractive index. The device is used as a light pipe in medical diagnosis and for optical signal transmission.

• A lens is a piece of transparent refracting material which is bounded by two spherical surfaces or by one spherical surface and one plane surface.

• When the lens is thicker in the middle than at the edges, it is called a convex lens or converging lens. When it is thinner in the middle, it is called a concave lens or diverging lens.

• The image formed by a concave lens is always virtual, erect and diminished and lies between the lens and F for all positions of the object.

• Lens’s maker's formula : 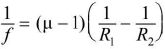where μ is the refractive index of the material of the lens with respect to the outer medium, R₁ is the radius of curvature of the surface facing the object and R₂ that of the other surface.

• Sign convention for radii of curvature - When the centre of curvature is on the same side as the outgoing light, R is positive, otherwise it is negative.

• The focal length of a convex lens is positive and that of a concave lens is negative.

• The lens equation is
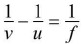
  where u is the distance of the object from the lens, v is the distance of the image from the lens and f is the focal length.

• Linear magnification is given as m = v/u.

• For a convex lens m is positive, when object lies between F and optical centre of lens, and image is virtual, m is negative when object lies beyond F and image is real.

• For a concave lens, m is positive as image is always erect and virtual.

• Areal magnification, m_A =

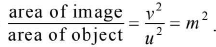
• The reciprocal of focal length of a lens is called its power. Power P= 1/f.

• If two thin lenses, having focal lengths f₁ and f₂ are placed in contact, then the equivalent focal length F of the combination is given by
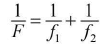   and power P = P₁ + P₂.

• When two thin lenses are separated along an axis by a distance x,
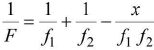
  P = P₁ + P₂ - x . P₁ P₂.

• As the refractive index is different for different colours, the image of an object illuminated by white light gets spread out. The violet colour is focussed nearest to the lens and the red farthest. This delect is known as chromatic aberration.

• In astigmatism, horizontal and vertical lines may be focussed in different planes.

• If an object not on the principal axis may not come to a sharp focus but converge in a comet shaped figure, the defect is called coma.

• Distortion happens due to non-uniform magnification of images at different points.

• A ray of light suffers two refractions at two surfaces on passing through a prism.

• Prism formula is given as
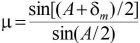
  where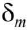  is the minimum deviation and A is the angle of the prism.

• Dispersion of light is the phenomenon of splitting of white light into its constituent colours on passing through a prism. This is because different colours have different wavelengths.

• Angular dispersion 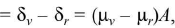 where μ_v and μ_r represents refractive index for violet and red lights.

• Dispersive power, ω is the mean refractive index.

• Spectra obtained from luminous bodies are called emission spectra. These are of three types.
  (i) Line spectrum : It consists of narrow bright lines separated by dark intervals.
  (ii) Band spectrum : It consists of a number of bright bands separated by dark intervals and contains a large number of close lines.
  (iii) Continuous spectrum : A continuous spectrum consists of an unbroken sequence of wavelength over a wide range.

• Absorption spectra - When white light passes through a semi-transparent solid, liquid or gas its spectrum contains certain dark lines or bands, showing that certain wavelengths have been absorbed. Such a spectra is called the absorption spectrum.

• The solar spectrum shows several dark lines crossing the otherwise continuous spectrum. These are called Fraunhofer lines.

• The amount of scattering by molecules (Rayleigh scattering) is inversely proportional to the fourth power of the wavelength.

The eye

• In myopia or short sightedness, only nearby objects can be seen distinctly. Far point of eye shifts from infinity to a distance d. To remove this defect, a concave lens of focal length (d) has to be used.

In hypermetropia or long-sightedness, only far off objects can be seen distinctly. Near point of eye shifts away from the eye. To remove this, a convex lens of focal length (f) has to be used.

Astigmatism - An astigmatic eye cannot focus on horizontal and vertical lines at the same distance at the same time. This can be corrected by using suitable cylindrical lenses.

Camera

• f-numbers
  (i) The f-numbers represent the size of the aperture.
  (ii) Usually,f-numbers are 2, 2.8, 4, 5.6, 8, 11, 22, 32.
  (iii) The diameter of aperture = d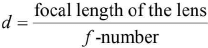
  

The amount of light (L) entering the camera is directly proportional to the area A of the aperture. A depends on diameter of aperture d.
L ∝ A ∝ d²

• Brightness of image B is proportional to d²/f².
  or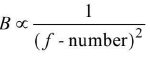
• Exposure number E determines time of exposure T.
  
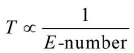
• Time of exposure T
  
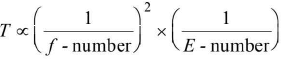
• Depth of focus
  It refers to the range of distance over which the object may lie so as to form a good quality image. Larger the /-numbers, greater will be the depth of focus.

Simple microscope

• A simple microscope consists of a convex lens of small focal length i.e. large power.
• Magnifying power = M
  (i) For distinct vision,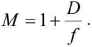
  The final image is formed at the least distance of distinct vision from eye.
  This distance D is about 25 cm.
  (ii) For normal vision,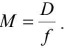
  The final image is formed at infinity for normal vision setting.

Compound microscope

• A compound microscope consists of an objective and an eyepiece.
  The objective is a convex lens of small focal length f₀.
  The eye-piece is a convex lens o f small focal length f_e but f₀, < f_e .
• Magnifying power for distinct vision
  
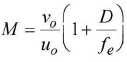
• Magnifying power for normal vision
  
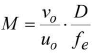
• Crosswires may be used for measurement purposes.
• The object is placed very near the objective but beyond the focus of objective.
• The objective forms a real, enlarged and inverted image of the object.
• This image serves as the virtual object for eyepiece of microscope.
• Final image is enlarged and inverted with respect to the object viewed by microscope.
• Resolving power of a microscope is given by
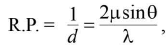   where d is the minimum distance between two point objects which can just be resolved, λ is the wavelength of light used, μ is the refractive index of the medium between the object and lens and 0 is the half angle of the cone of light from the point object on the objective lens.

Telescope

• A telescope consists of an objective and an eyepiece.
  The objective is a convex lens of large focal length and large aperture. The eyepiece is a convex lens of small focal length.
  f_o > f_e.
• Magnifying power for distinct vision
  
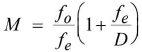
  The object lies at infinity.

  The focal image is formed at least distance of distinct vision (D).

• Magnifying power for normal vision
  
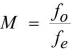
  The object lies at infinity.
  The final image is also formed at infinity.
  Tube length = f₀ + f_e.

• Resolving power of telescope
  (i) The ability of an optical instrument to produce separate diffraction patterns of two nearby objects is known as resolving power.
  (ii) The reciprocal of resolving power is defined as the limit of resolution.
  (iii) For telescope,
  the limit of resolution (dθ) =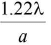
  Resolving power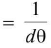
  or Resolving power =
  (iv) dθ ∝ λ (wavelength of light used)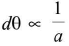
  (d = diameter of aperture of objective).

Salient points about ray optics

• Continuous spectrum is produced by red hot bodies, electric bulbs, electric arc, sun, red hot gases etc.
• Band/molecular spectrum is produced by gases excited in molecular form. Discharge tubes containing gases at low pressure produce band spectra.
• Line spectrum is produced by substances excited in atomic form. Lamps of sodium and mercury give line spectra.
• When light is reflected by a denser medium, phase difference of π radian or path difference of λ/2 or time difference T/2 is produced. This is known as Stoke's law.
• Path of light is reversible.
• Distance x travelled by light in a medium o f refractive index μ is equal to distance (μx) travelled in vacuum.
• Time taken by light to traverse a thickness x of medium of refractive index μ,
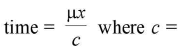   velocity of light in vacuum.
• Cauchy's formula:
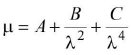
  μ denotes refractive index and X denotes wavelength of light.
  Generally speaking,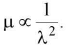
• Illustration of scattering of light
  (i) Blue colour of sky
  (ii) Red colour of signals of danger
  (iii) Red colour at the time of sun-rise and sun-set
  (iv) Black colour of sky in the absence of atmosphere
• The human eye is most sensitive to yellow colour.
• For large magnifying power of a telescope,f_o should be large and f_e should be small.
• For large magnifying power o f a microscope, f₀ < f_e but f_e should be small.
• Eye-pieces
  (i) Huygen's eye piece is free from chromatic and spherical aberrations but it cannot be used for measurement purposes.
  (ii) Ramsden's eye piece can be used for precise measurement as cross wires can be fixed in this eye-piece. It slightly suffers from spherical and chromatic aberrations.