Important Determinant Formulas Formulas for JEE and NEET

Important Formulas
1.The symbol  is called the determinant of order two.
is called the determinant of order two.
It's value is given by : D = a1 b2 − a2 b1
2.The symbol 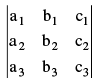 is called the determinant of order three.
is called the determinant of order three.
Its value can be found as : D = 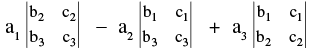
Or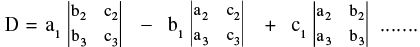 and so on. In this manner we can expand a determinant in 6 ways using elements of ; R1, R2, R3 or C1, C2, C3.
and so on. In this manner we can expand a determinant in 6 ways using elements of ; R1, R2, R3 or C1, C2, C3.
3. The following examples of short handwriting large expressions are :
(i) The lines : a1x + b1y + c1 = 0........ (1)
a2x + b2y + c2 = 0........ (2)
a3x + b3y + c3 = 0........ (3)
are concurrent if, 
Condition for the consistency of three simultaneous linear equations in 2 variables.
(ii) ax2+ 2 hxy + by2 + 2 gx + 2 fy + c = 0 represents a pair of straight lines if abc + 2 fgh − af2 − bg2 − ch2 = 0 = 
(iii) The area of a triangle whose vertices are (xr, yr) ; r = 1 , 2 , 3 is : 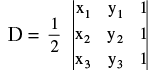 If D = 0 then the three points are collinear.
If D = 0 then the three points are collinear.
(iv) Equation of a straight line passing through 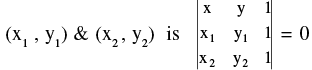
4. Minor
The minor of a given element of a determinant is the determinant of the elements which remain after deleting the row & the column in which the given element stands For example, the minor of a1 in (Key Concept 2) is 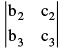 & the minor of b2 is
& the minor of b2 is
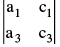 . Hence a determinant of order two will have “4 minors” & a determinant of order three will have “9 minors” .
. Hence a determinant of order two will have “4 minors” & a determinant of order three will have “9 minors” .
5. Cofactor If Mij represents the minor of some typical element then the cofactor is defined as :
Cij = (−1)i+j . Mij ; Where i & j denotes the row & column in which the particular element lies. Note that the value of a determinant of order three in terms of ‘Minor’ & ‘Cofactor’ can be written as : D = a11M11 − a12M12 + a13M13 OR D = a11C11 + a12C12 + a13C13 & so on .......
6. Properties of Determinants
Property −1 : The value of a determinant remains unaltered, if the rows & columns are inter changed. e.g. if D = 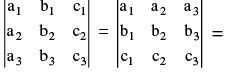 D′ D & D′ are transpose of each other. If D′ = − D then it is SKEW SYMMETRIC determinant but D′ = D ⇒ 2 D = 0 ⇒ D = 0 ⇒ Skew symmetric determinant of third order has the value zero.
D′ D & D′ are transpose of each other. If D′ = − D then it is SKEW SYMMETRIC determinant but D′ = D ⇒ 2 D = 0 ⇒ D = 0 ⇒ Skew symmetric determinant of third order has the value zero.
Property -2 : If any two rows (or columns) of a determinant be interchanged, the value of determinant is changed in sign only. e.g. Let: 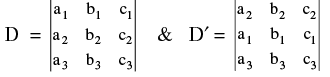 Then D′ = − D.
Then D′ = − D.
Property -3 : If a determinant has any two rows (or columns) identical, then its value is zero. e.g. Let D = 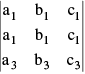 then it can be verified that D = 0.
then it can be verified that D = 0.
Property -4 : If all the elements of any row (or column) be multiplied by the same number, then the determinant is multiplied by that number.
e.g. If D 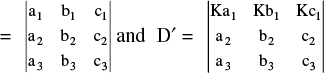 Then D′= KD
Then D′= KD
Property -5 : If each element of any row (or column) can be expressed as a sum of two terms then the determinant can be expressed as the sum of two determinants. e.g. 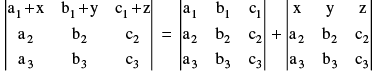
Property -6 : The value of a determinant is not altered by adding to the elements of any row (or column) the same multiples of the corresponding elements of any other row (or column).e.g. Let D 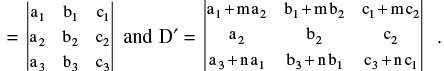 Then D′ = D.
Then D′ = D.
Note : that while applying this property ATLEAST ONE ROW (OR COLUMN) must remain unchanged.
Property -7 : If by putting x = a the value of a determinant vanishes then (x − a) is a factor of the determinant.
7. Multiplicaion of Determinants
(i) 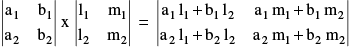 Similarly two determinants of order three are multiplied.
Similarly two determinants of order three are multiplied.
(ii) If D = 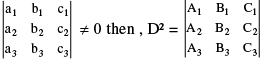 where Ai, Bi, Ci are cofactors
where Ai, Bi, Ci are cofactors
PROOF : Consider 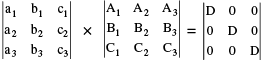 Note : a1A2 + b1B2 + c1C2 = 0 etc. therefore,
Note : a1A2 + b1B2 + c1C2 = 0 etc. therefore, 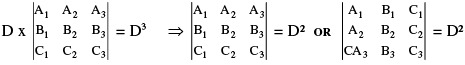
8. System of Linear Equations(In Two Variables)
(i) Consistent Equations: Definite & unique solution. [intersecting lines]
(ii) Inconsistent Equation: No solution. [Parallel line]
(iii) Dependent Equation : Infinite solutions. [Identical lines]
Let a1x + b1y + c1 = 0 & a2x + b2y + c2 = 0 then :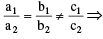 Given equations are inconsistent &
Given equations are inconsistent &  Given equations are dependent
Given equations are dependent
9. Cramer's Rule
Let, a1x + b1y + c1z = d1 ...(I) ; a2x + b2y + c2z = d2 ... (II) ; a3x + b3y + c3z = d3 ... (III)
Then, 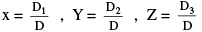 .
.
Where 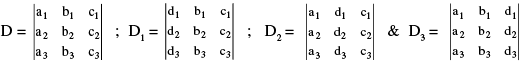
NOTE : (a) If D ≠ 0 and alteast one of D1, D2, D3 ≠ 0, then the given system of equations are consistent and have unique non trivial solution.
(b) If D ≠ 0 & D1 = D2 = D3 = 0, then the given system of equations are consistent and have trivial solution only.
(c) If D = D1 = D2 = D3 = 0, then the given system of equations are consistentand have infinite solutions. In case 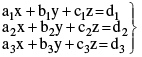 represents these parallel planes then also D = D1 = D2 = D3 = 0 but the system is inconsistent.
represents these parallel planes then also D = D1 = D2 = D3 = 0 but the system is inconsistent.
(d) If D = 0 but at least one of D1, D2, D3 is not zero then the equations are in consistent and have no solution.
10. If x, y, z are not all zero, the condition for a1x + b1y + c1z = 0 ; a2x + b2y + c2z = 0 & a3x + b3y + c3z = 0 to be consistent in x, y, z is that 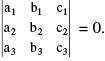 Remember that if a given system of linear equations have Only Zero Solution for all its variables then the given equations are said to have trivial solution.
Remember that if a given system of linear equations have Only Zero Solution for all its variables then the given equations are said to have trivial solution.
|
176 videos|582 docs|160 tests
|
FAQs on Important Determinant Formulas Formulas for JEE and NEET
| 1. What is a determinant in linear algebra? |  |
| 2. How do you calculate the determinant of a 2x2 matrix? |  |
| 3. What is the geometric interpretation of the determinant? |  |
| 4. Can you explain how to find the determinant of a 3x3 matrix? |  |
| 5. What properties of determinants should I know? |  |
















