Formulas - Relations and Functions - JEE PDF Download

1. General  Definition:

If to every value (Considered as real unless other−wise stated) of a variable x, which belongs to some collection (Set) E, there corresponds one and  only one  finite value of the quantity y, then  y is said to be a function (Single valued) of x or a dependent variable defined on the set E ;  x is the argument or independent variable .

If to every value of x belonging to some set E there corresponds one or several values of the variable y, then y is called a multiple valued function of x defined on E.Conventionally the word "Function” is used only as the  meaning  of a  single  valued function, if not otherwise stated. Pictorially: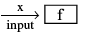  

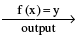 , y is called the image of x & x is the pre-image of y under f.  Every function from A  → B satisfies the following conditions .

(i) f ⊂  A x B  (ii) ∀  a ∈ A ⇒ (a, f(a)) ∈ f  and (iii)(a, b) ∈ f   &   (a, c) ∈ f  ⇒  b = c

2. Domain,  CO−−−−Domain  &  Range  Of  A  Function:

Let f :  A → B, then  the  set  A is  known  as the domain of f & the set B is known as co-domain off . The set of all f images of elements of A is known as the range off . Thus
Domain of f = {a| a ∈ A, (a, f(a)) ∈ f}
Range of f = {f(a) |a ∈ A, f(a) ∈ B} 

It should be noted that range is a subset of co−domain . If only the rule of function is given then the domain of the function is the set of those real numbers, where function is defined. For a continuous function, the interval from minimum to maximum value of a function gives the range.

3. Important  Types of   Functions :

(i) Polynomial  Function : If a function f is defined by f (x) = a₀ xⁿ + a₁ xⁿ⁻¹ + a₂ xⁿ⁻² + ... + a_n−1 x + a_n where n is a non negative integer and a₀, a₁, a₂, ..., a_n are real numbers and a₀ ≠ 0, then f is called a polynomial function of degree n NOTE : (a) A polynomial of degree one with no constant term is called an odd linear function .  i.e.  f(x) = ax ,  a ≠ 0.

(b) There  are  two polynomial  functions , satisfying  the  relation ; f(x).f(1/x) = f(x) + f(1/x).  They are  :
(i)  f(x) = xⁿ + 1  & (ii)  f(x) = 1 − xⁿ  , where n is a positive integer .
(ii) Algebraic Function : y is an algebraic function of x, if it is a function that satisfies an algebraic equation of the form P₀ (x) yⁿ + P₁ (x) yⁿ⁻¹ + ....... + P_n−1 (x) y + P_n (x) = 0  Where n is a positive integer and P₀ (x), P₁ (x) ........... are Polynomials in x.
e.g.  y = |x| is an algebraic function, since it satisfies the equation y² − x² = 0.

Note that all polynomial functions are Algebraic but not the converse. A function that is not algebraic is called Transcedental  Function.

(iii) Fractional  Rational  Function: A rational function is a function of the form. y =  f (x)  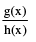=  where g (x) & h (x) are polynomials  & h (x) ≠ 0.

(iv) Absolute  Value  Function: A function y = f (x) = |x| is called  the  absolute  value  function  or  Modulus function.  It is defined as :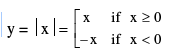

(V) Exponential  Function : A  function  f(x) = a^x = e^{x ln a} (a > 0 ,a ≠ 1, x ∈ R) is called an exponential function. The inverse of the exponential function is called the logarithmic function . i.e. g(x) = log_a x .

Note that  f(x) & g(x) are inverse of each other & their graphs are as shown .
   

(vi) Signum  Function : A function y= f (x) = Sgn (x) is defined as follows :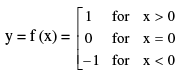

It is also written as Sgn x = |x|/ x  ;  x ≠ 0 ;  f (0) = 0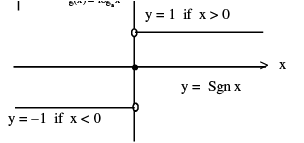

(vii) Greatest  Integer  or Step Up  Function : The function  y = f (x) = [x]  is called the greatest integer  function where [x]  denotes the greatest integer less than or equal to x . Note that for :

Properties of  greatest  integer function :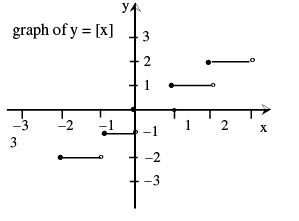

(a) [x] ≤ x < [x] + 1   and 

x − 1 < [x] ≤ x ,  0 ≤ x − [x] < 1

(b) [x + m] = [x] + m   if m is an integer . 

(c) [x] + [y] ≤ [x + y] ≤ [x] + [y] + 1 

(d) [x] + [− x] = 0   if x is an integer = − 1  otherwise .

(viii) Fractional  Part  Function : It  is  defined  as : g (x) = {x} = x − [x] . e.g. the fractional part of the no. 2.1 is 2.1− 2 = 0.1 and the fractional part  of − 3.7 is 0.3.  The period of this function is 1 and graph of thi s function is as shown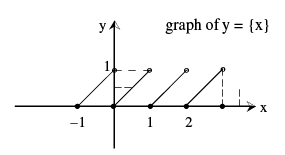
 

4. Domains  And Ranges of Common Function :

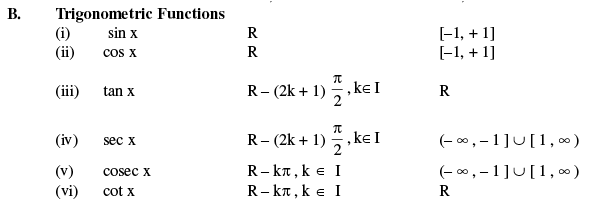
J. Constant Function

say f (x) = c                                     R                              { c }

5. Equal  Or  Identical  Function :

Two functions  f  &  g  are said to be equal  if : 

(i) The domain of  f  =  the domain of  g. 

(ii) The range of  f  =  the range of  g  and 

(iii) f(x) = g(x)  ,  for every x belonging to their common domain.  eg.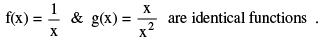

6. Classification  of  Functions : One −−−− One Function (Injective mapping) : A function  f :  A → B is said to be  a one−one  function  or  injective mapping if different  elements of  A have different f images in B .  Thus for  x₁, x₂ ∈ A &  f(x1) , f(x₂) ∈ B ,  f(x₁) = f(x₂)  ⇔  x₁ = x₂   or  x₁ ≠ x₂ ⇔  f(x₁) ≠  f(x₂) .

Diagramatically an injective mapping can be shown as

Note : 

(i) Any function which is entirely increasing or decreasing in whole domain, then f(x) is one−one . 

(ii) If any line parallel to x−axis cuts the graph of the function at most at one point, then the function is one−one .

Many–one function : A function  f :  A → B  is  said  to  be  a  many  one  function  if two or more elements of A have  the  same f image in  B . Thus  f :  A → B is  many  one  if for ;  x₁, x₂ ∈ A ,  f(x₁) = f(x₂) but  x₁ ≠ x₂ 

Diagramatically a many one mapping can be shown as

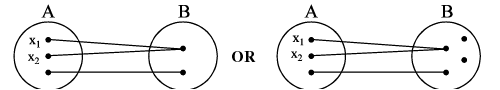
Note :

(i) Any continuous function which has at least one local maximum or local minimum, t h e n f( x ) is many−one . In  other  words,  if  a line parallel to x−axis  cuts  the  graph  of the  function  at least at  two  points, then f is many−one .,

(ii) If a function is one−one, it cannot be many−one and vice versa .

Onto function (Surjective mapping) : If the function  f :  A → B is such that each element in B (co−domain) is the f image of at least one element in A, then we say that f is a function of A 'onto' B . Thus f : A → B is surjective if f   ∀  b ∈ B,  ∃ some  a ∈ A such that  f (a) = b .

Diagramatically surjective mapping can be shown as

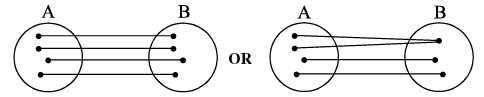
Note that : if range = co−domain, then  f(x) is onto. Into function : If  f :  A → B is such that there exists at least one element in co−domain which is not the image of any element in domain, then  f(x) is into .

Diagramatically into function can be shown as

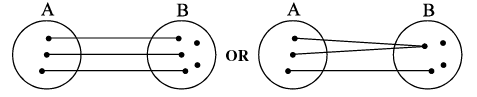
Note that : If a function is onto, it cannot be into and vice versa . A polynomial of degree even will always be into. Thus a function can be one of these four types :

(a) one−one onto (injective & surjective)  

(b) one−one into (injective but not surjective)

(c) many−one onto (surjective but not injective)

(d) many−one into (neither surjective nor injective)  

Note :

(i) If f is both injective & surjective, then it is called a Bijective mapping.

The bijective functions  are  also  named  as  invertible,  non singular  or bi uniform functions. 

(ii) If a  set  A contains n distinct  elements  then  the  number  of  different  functions defined from A → A is nⁿ & out of it n ! are one one.

Identity function : The function  f :  A → A defined by  f(x) = x  ∀  x ∈ A is called the identity of A and is denoted by IA. It is easy to observe that identity function is a bijection .

Constant function: A function  f :  A → B is said to be a constant function if every element of A has the same f image in B . Thus  f :  A → B ;  f(x) = c ,  ∀  x ∈ A ,  c ∈ B  is a constant function. Note that the range of a constant function is a singleton and a constant function may be  one-one or many-one, onto or into . 

7. Algebraic  Operations  on  Functions :

If f & g are real valued functions of x with domain set A, B respectively, then both f & g are defined in A ∩ B. Now we define f + g ,  f − g ,  (f . g) & (f/g) as follows :

(i) (f ± g) (x) = f(x) ± g(x)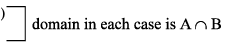  

(ii) (f . g) (x) = f(x) . g(x)

(iii) 

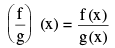  domain is  {x | x ∈ A ∩ B  s . t  g(x) ≠ 0} .

8. Composite Of Uniformly & Non - Uniformly Defined Functions:

Let  f :  A → B  &  g : B → C  be two functions . Then the function gof :  A → C  defined by  (gof) (x) = g (f(x))  ∀  x ∈ A  is called the composite of the two functions f & g .

Diagramatically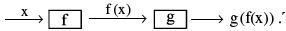

Thus  the  image  of  every  x ∈ A under the function gof is the g−image of the f−image of x .Note that g of is defined only if  ∀  x ∈ A,  f(x) is an element of the domain of g so that we can take its g-image. Hence for the product gof of two functions f & g, the range of f must be a subset of the domain of g. 

Properties  of Composite  Functions: 

(i) The composite of functions is not commutative  i.e.  gof ≠ fog . 

(ii) The composite of functions is associative i.e. if  f, g, h are three functions such that fo (goh) & (fog) oh are defined, then  fo (goh) = (fog) oh .

(iii) The composite  of  two bijections is a bijection i.e.  if f & g are two bijections such that gof is defined, then gof is also a bijection.

9. Homogeneous  Functions:

A function  is  said  to  be  homogeneous  with  respect  to  any  set  of  variables when  each  of  its  terms is  of  the  same  degree  with  respect  to  those  variables  .

For  example  5 x² + 3y² − xy  is  homogeneous  in  x & y . Symbolically if , f (tx , ty) = tn . f (x , y)  then f (x , y) is homogeneous function of degree n .

10. Bounded Function:

A function is said to be bounded if |f(x)| ≤ M , where M is a finite quantity .

11. Implicit  &  Explicit  Function:

A function  defined  by an  equation  not  solved for the dependent variable is called an Implicit Function . For eg. the equation  x³ + y³ = 1 defines  y  as an implicit  function. If y has been expressed in terms of x alone then it is called an Explicit  Function. 

12. Inverse  Of  a  Function : Let  f :  A → B  be a  one−one  &  onto function,  then  their  exists a  unique  function g :  B → A  such that  f(x) = y ⇔ g(y) = x,  ∀  x ∈ A  &  y ∈ B .  Then g is said to be inverse of f .  Thus g = f⁻¹ :  B → A =  {(f(x), x) | (x,  f(x)) ∈ f} .

Properties of  Inverse  Function : 

(i) The inverse of a bijection is unique . 

(ii) If  f :  A → B  is a bijection & g :  B → A is the inverse of f, then  fog = IB and gof = I_A ,  where  I_A &  I_B are identity functions on the sets A & B respectively.

Note  that  the  graphs  of  f & g  are  the  mirror  images  of  each  other  in  the line  y = x . As shown in the figure given below a point (x ',y ' ) corresponding to y = x² (x >0) changes to (y ',x ' ) corresponding to y = + x , the changed form of  x =√ y .

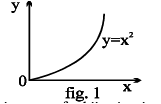
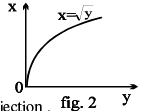
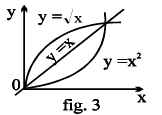
(iii) The inverse of a bijection is also a bijection . 

(iv) If f & g  two bijections  f :  A → B ,  g :  B → C  then the inverse of gof exists and  (gof)−1 = f−1o g−1 13. 

Odd &  Even  Functions : If  f (−x) = f (x) for all x in the domain of ‘f’ then f is said to be an even function. e.g. f (x) = cos x  ;  g (x) = x² + 3 . If f (−x) = −f (x) for all x in the domain of ‘f’ then f is said to be an odd function. e.g. f (x) = sin x  ;   g (x) = x³ + x .

NOTE : 

(a) f (x) − f (−x) = 0 ⇒  f (x) is even  &  f (x) + f (−x) = 0 ⇒ f (x) is odd . 

(b) A function may neither be odd nor even .

(c)Inverse  of  an  even  function  is  not  defined 

(d) Every even function is symmetric about the y−axis  &  every odd  function is symmetric about the origin.

(e) Every function can be expressed as the sum of an even & an odd function.

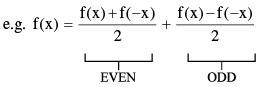
(f) only function which is defined on the entire number line & is even and odd at the same time is f(x)= 0. (g) If f and g both  are even or both are odd then the function  f.g  will  be even but if any one of them is odd then f.g  will  be odd .

14. Periodic Function : A function  f(x) is  called  periodic  if  there exists a positive number T (T > 0) called the period  of the  function  such  that  f (x + T) = f(x),  for  all  values  of  x within the domain of x e.g. The function sin x & cos x both are periodic over 2π & tan x is periodic over π 

NOTE: 

(a) f (T) = f (0) = f (−T) ,  where ‘T’ is the period .

(b) Inverse of a periodic function does not exist .

(c) Every constant function is always periodic, with no fundamental period.

(d) If  f (x)  has  a period  T  &  g (x)  also  has  a  period T  then it does not  mean that   f (x) + g (x) must have a period T .   e.g.  f(x) = |sinx| + |cosx|. 

(e) If  f(x) has a period p, then  also has a period p.

(f) if  f(x) has a period T then f(ax + b) has a period  T/a  (a > 0) .

15. General: If  x, y are independent variables, then : 

(i) f(xy) = f(x) + f(y)   ⇒  f(x) = k ln x  or   f(x) = 0 . 

(ii) f(xy) = f(x) . f(y)   ⇒  f(x) = x_n ,  n ∈ R

(iii) f(x + y) = f(x) . f(y)  ⇒  f(x) = a^kx . 

(iv) f(x + y) = f(x) + f(y)  ⇒  f(x) = kx,  where k is a constant .