Important Application of Derivatives Formulas Formulas for JEE and NEET
Things To Remember :
(i) The value of the derivative at P (x1 , y1) gives the slope of the tangent to the curve at P. Symbolically 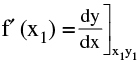 = Slope of tangent at P (x1 y1) = m (say).
= Slope of tangent at P (x1 y1) = m (say).
(ii) Equation of tangent at (x1, y1) is ; 
(iii) Equation of normal at (x1, y1) is ; 
Note :
1.The point P (x1 , y1) will satisfy the equation of the curve & the eqation of tangent & normal line.
2. If the tangent at any point P on the curve is // to the axis of x then dy/dx = 0 at the point P.
3. If the tangent at any point on the curve is parallel to the axis of y, then dy/dx = ∞ or dx/dy = 0.
4. If the tangent at any point on the curve is equally inclined to both the axes then dy/dx = ± 1.
5. If the tangent at any point makes equal intercept on the coordinate axes then dy/dx = – 1.
6. Tangent to a curve at the point P (x1, y1) can be drawn even through dy/dx at P does not exist. e.g. x = 0 is a tangent to y = x2/3 at (0, 0).
7. If a curve passing through the origin be given by a rational integral algebraic equation, the equation of the tangent (or tangents) at the origin is obtained by equating to zero the terms of the lowest degree in the equation. e.g. If the equation of a curve be x2 – y2 + x3 + 3 x2 y − y3 = 0, the tangents at the origin are given by x2 – y2 = 0 i.e. x + y = 0 and x − y = 0.
(iv) Angle of intersection between two curves is defined as the angle between the 2 tangents drawn to the 2 curves at their point of intersection. If the angle between two curves is 90° every where then they are called ORTHOGONAL curves.
(v) (a) Length of the tangent (PT) = 
(b) Length of Subtangent (MT) = 
(c) Length of Normal (PN) = 
(d) Length of Subnormal (MN) = y1 f ' (x1)
(vi) Differentials :
The differential of a function is equal to its derivative multiplied by the differential of the independent variable. Thus if, y = tan x then dy = sec2 x dx.
In general dy = f ′ (x) d x.
Note that : d (c) = 0 where 'c' is a constant.
d (u + v − w) = du + dv − dw d (u v) = u d v + v d u
Note :
1. For the independent variable 'x' , increment ∆ x and differential d x are equal but this is not the case with the dependent variable 'y' i.e. ∆ y ≠ d y.
2. The relation d y = f ′ (x) d x can be written as  (x) ; thus the quotient of
(x) ; thus the quotient of
the differentials of 'y' and 'x' is equal to the derivative of 'y' w.r.t. 'x'.
Monotonocity
(Significance of the sign of the first order derivative)
Definitions :
1. A function f (x) is called an Increasing Function at a point x = a if in a sufficiently small neighbourhood
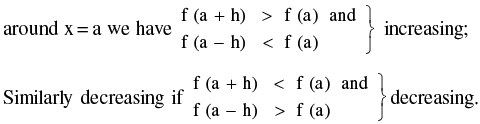
2. A differentiable function is called increasing in an interval (a, b) if it is increasing at every point within the interval (but not necessarily at the end points). A function decreasing in an interval (a, b) is similarly defined.
3. A function which in a given interval is increasing or decreasing is called “Monotonic” in that interval.
4. Tests for increasing and decreasing of a function at a point :
If the derivative f ′(x) is positive at a point x = a, then the function f (x) at this point is increasing. If it is negative, then the function is decreasing. Even if f ' (a) is not defined, f can still be increasing or decreasing.

Note : If f ′(a) = 0, then for x = a the function may be still increasing or it may be decreasing as shown. It has to be identified by a seperate rule. e.g. f (x) = x3 is increasing at every point. Note that, dy/dx = 3 x².
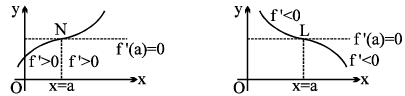
5. Tests for Increasing & Decreasing of a function in an interval :
Sufficiency Test :
If the derivative function f ′(x) in an interval (a , b) is every where positive, then the function f (x) in this interval is Increasing ; If f ′(x) is every where negative, then f (x) is Decreasing.
General Note :
(1) If a function is invertible it has to be either increasing or decreasing.
(2) If a function is continuous the intervals in which it rises and falls may be separated by points at which its derivative fails to exist.
(3) If f is increasing in [a, b] and is continuous then f (b) is the greatest and f (c) is the least value of f in [a, b]. Similarly if f is decreasing in [a, b] then f (a) is the greatest value and f (b) is the least value.
6. (a) ROLLE'S THEOREM :
Let f(x) be a function of x subject to the following conditions :
(i) f(x) is a continuous function of x in the closed interval of a ≤ x ≤ b.
(ii) f ′ (x) exists for every point in the open interval a < x < b.
(iii) f (a) = f (b). Then there exists at least one point x = c such that a<c < b where f ′ (c) = 0.
Note that if f is not continuous in closed [a, b] then it may lead to the adjacent graph where all the 3 conditions of Rolles will be valid but the assertion will not be true in (a, b).
(b) LMVT THEOREM :
Let f(x) be a function of x subject to the following conditions :
(i) f(x) is a continuous function of x in the closed interval of a ≤ x ≤ b.
(ii) f ′ (x) exists for every point in the open interval a < x < b.
(iii) f(a) ≠ f(b).
Then there exists at least one point x = c such that a < c < b where f ′ (c) 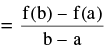
Geometrically, the slope of the secant line joining the curve at x = a & x = b is equal to the slope of the tangent line drawn to the curve at x = c. Note the following :
- Rolles theorem is a special case of LMVT since
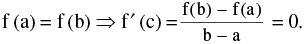
Note :
Now [f (b) – f (a)] is the change in the function f as x changes from a to b so that [f (b) – f (a)] / (b – a) is the average rate of change of the function over the interval [a, b]. Also f '(c) is the actual rate of change of the function for x = c. Thus, the theorem states that the average rate of change of a function over an interval is also the actual rate of change of the function at some point of the interval. In particular, for instance, the average velocity of a particle over an interval of time is equal to the velocity at some instant belonging to the interval. This interpretation of the theorem justifies the name "Mean Value" for the theorem.
(c) Application Of Rolles Theorem For Isolating The Real Roots Of An Equation F (X)=0
Suppose a & b are two real numbers such that ;
(i) f(x) & its first derivative f ′ (x) are continuous for a ≤ x ≤ b.
(ii) f(a) & f(b) have opposite signs.
(iii) f ′ (x) is different from zero for all values of x between a & b.
Then there is one & only one real root of the equation f(x) = 0 between a & b.
Maxima - Minima
Functions Of A Single Variable
How Maxima & Minima Are Classified
1. A function f(x) is said to have a maximum at x = a if f(a) is greater than every other value assumed by f(x) in the immediate neighbourhood of x = a. Symbolically 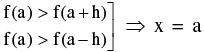 gives maxima for a sufficiently small positive h.
gives maxima for a sufficiently small positive h.
Similarly, a function f(x) is said to have a minimum value at x = b if f(b) is least than every other value assumed by f(x) in the immediate neighbourhood at x = b. Symbolically if  = b gives minima for a sufficiently small positive h.
= b gives minima for a sufficiently small positive h.
Note that :

(i) the maximum & minimum values of a function are also known as local/relative maxima or local/relative minima as these are the greatest & least values of the function relative to some neighbourhood of the point in question.
(ii) the t erm 'extremum' or (extremal) or 'turning value' is used both for maximum or a minimum value.
(iii) a maximum (minimum) value of a function may not be the greatest (least) value in a finite interval.
(iv) a function can have several maximum & minimum values & a minimum value may even be greater than a maximum value.
(v) maximum & minimum values of a continuous function occur alternately & between two consecutive maximum values there is a minimum value & vice versa.
2. A Necessary Condition For Maximum & Minimum :
If f(x) is a maximum or minimum at x = c & if f ′ (c) exists then f ′ (c) = 0.

Note :
(i) The set of values of x for which f ′ (x) = 0 are often called as stationary points or critical points. The rate of change of function is zero at a stationary point.
(ii) In case f ′ (c) does not exist f(c) may be a maximum or a minimum & in this case left hand and right hand derivatives are of opposite signs.
(iii) The greatest (global maxima) and the least (global minima) values of a function f in an interval [a, b] are f(a) or f(b) or are given by the values of x for which f ′ (x) = 0.
(iv) Critical points are those where  = 0, if it exists ,or it fails to exist either by virtue of a vertical tangent or by virtue of a geometrical sharp corner but not because of discontinuity of function.
= 0, if it exists ,or it fails to exist either by virtue of a vertical tangent or by virtue of a geometrical sharp corner but not because of discontinuity of function.
3. Sufficient Condition For Extreme Values : is a point of local maxima, where f ′ (c) = 0.
is a point of local maxima, where f ′ (c) = 0.
Similarly 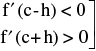 ⇒ x = c is a point of local minima, where f ′(c) = 0.
⇒ x = c is a point of local minima, where f ′(c) = 0.
Note : If f ′ (x) does not change sign i.e. has the same sign in a certain complete neighbourhood of c, then f(x) is either strictly increasing or decreasing throughout this neighbourhood implying that f(c) is not an extreme value of f.
4. Use Of Second Order Derivative In Ascertaining The Maxima Or Minima:
(a) f(c) is a minimum value of the function f, if f ' (c) = 0 & f '' (c) > 0.
(b) f(c) is a maximum value of the function f, f ' (c) = 0 & f '' (c) < 0.
Note : if f '' (c) = 0 then the test fails. Revert back to the first order derivative check for ascertaning the maxima or minima.
5. SUMMARY-WORKING RULE :
FIRST :
When possible , draw a figure to illustrate the problem & label those parts that are important in the problem. Constants & variables should be clearly distinguished.
SECOND:
Write an equation for the quantity that is to be maximised or minimised. If this quantity is denoted by ‘y’, it must be expressed in terms of a single independent variable x. his may require some algebraic manipulations.
THIRD :
If y = f (x) is a quantity to be maximum or minimum, find those values of x for which dy/dx = f '(x) = 0.
FOURTH :
Test each values of x for which f '(x) = 0 to determine whether it provides a maximum or minimum or neither. The usual tests are :
(a) If d2y/dx2 is positive when dy/dx = 0 ⇒ y is minimum.
If d2y/dx2 is negative when dy/dx = 0 ⇒ y is maximum.
If d2y/dx2 = 0 when dy/dx = 0, the test fails.
(b) 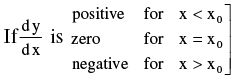 ⇒ a maximum occurs at x = x0.
⇒ a maximum occurs at x = x0.
But if dy/dx changes sign from negative to zero to positive as x advances through xo there is a minimum. If dy/dx does not change sign, neither a maximum nor a minimum. Such points are called INFLECTION POINTS.
FIFTH :
If the function y = f (x) is defined for only a limited range of values a ≤ x ≤ b then examine x = a & x = b for possible extreme values.
SIXTH :
If the derivative fails to exist at some point, examine this point as possible maximum or minimum.
Important Note :
– Given a fixed point A(x1, y1) and a moving point P(x, f (x)) on the curve y = f(x). Then AP will be maximum or minimum if it is normal to the curve at P.
– If the sum of two positive numbers x and y is constant than their product is maximum if they are equal, i.e. x + y = c , x > 0 , y > 0 , then
– If the product of two positive numbers is constant then their sum is least if they are equal. i.e. (x + y)2 = (x – y)2 + 4xy
6. Useful Formulae Of Mensuration To Remember :
- Volume of a cuboid = lbh.
- Surface area of a cuboid = 2 (lb + bh + hl).
- Volume of a prism = area of the base x height.
- Lateral surface of a prism = perimeter of the base x height.
- Total surface of a prism = lateral surface + 2 area of the base
(Note that lateral surfaces of a prism are all rectangles). - Volume of a pyramid = 1/3 area of the base x height.
- Curved surface of a pyramid = 1/2 (perimeter of the base) x slant height.
(Note that slant surfaces of a pyramid are triangles). - Volume of a cone =

- Curved surface of a cylinder = 2 π rh.
- Total surface of a cylinder = 2 π rh + 2 π r2.
- Volume of a sphere =

- Surface area of a sphere = 4 π r2.
- Area of a circular sector =
 when θ is in radians.
when θ is in radians.
7. Significance Of The Sign Of 2nd Order Derivative And Points Of Inflection :
The sign of the 2nd order derivative determines the concavity of the curve. Such points such as C & E on the graph where the concavity of the curve changes are called the points of inflection. From the graph we find that if:
(i) 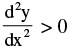 ⇒ concave upwards
⇒ concave upwards
(ii)  concave downwards.
concave downwards.
At the point of inflection we find that
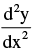 changes sign.
changes sign.
Inflection points can also occur if  fails to exist. For example, consider the graph of the function defined as,
fails to exist. For example, consider the graph of the function defined as,
Note that the graph exhibits two critical points one is a point of local maximum & the other a point of inflection.
|
172 videos|476 docs|154 tests
|





















