Important Limit and Continuity & Differentiability of Function Formulas for JEE and NEET
Things To Remember :
1. Limit of a function f(x) is said to exist as, x→a when 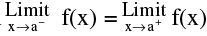 = finite quantity.
= finite quantity.
2. Fundamental Theorems On Limits:
Let 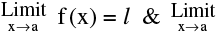 g (x) = m. If l & m exists then :
g (x) = m. If l & m exists then :
(i) 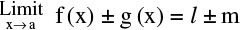
(ii) 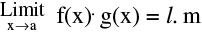
(iii)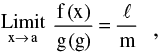 provided m ≠ 0
provided m ≠ 0
(iv)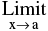 kf(x) = k
kf(x) = k 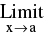 f(x) ; where k is a constant.
f(x) ; where k is a constant.
(v)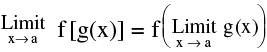 = f (m) ; provided f is continuous at g (x) = m.
= f (m) ; provided f is continuous at g (x) = m.
For example 
3. Standard Limits :
(a) 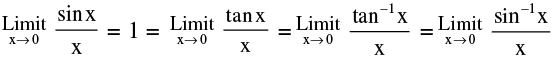 [ Where x is measured in radians ]
[ Where x is measured in radians ]
(b) 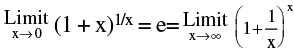 note however the re
note however the re (1 - h )n = 0and
(1 - h )n = 0and
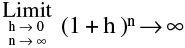
(c) If 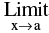 f(x) = 1 and
f(x) = 1 and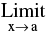 Ф (x) = ∞ , then ;
Ф (x) = ∞ , then ;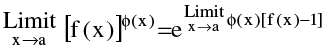
(d) If 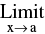 f(x) = A > 0 &
f(x) = A > 0 & 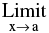 Ф (x) = B (a finite quantity) then ;
Ф (x) = B (a finite quantity) then ;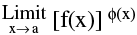 = ez where z =
= ez where z = 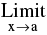 Ф (x). ln[f(x)] = eBlnA = AB
Ф (x). ln[f(x)] = eBlnA = AB
(e) 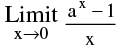 = 1n a (a > 0). In particular
= 1n a (a > 0). In particular 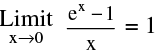
(f)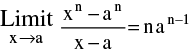
4. Squeeze Play Theorem :
If f(x) ≤ g(x) ≤ h(x) ∀ x & 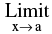 f(x) = l =
f(x) = l =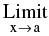 h(x) then
h(x) then 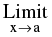 g(x) = l.
g(x) = l.
5. Indeterminant Forms :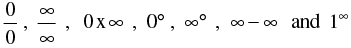
Note :
(i) We cannot plot ∞ on the paper. Infinity (∞) is a symbol & not a number. It does not obey the laws of elementry algebra.
(ii) ∞ + ∞ = ∞
(iii) ∞ × ∞ = ∞
(iv) (a/∞) = 0 if a is finite
(v) a/0 is not defined, if a ≠ 0.
(vi) ab = 0 , if & only if a = 0 or b = 0 and a & b are finite.
6. The following strategies should be born in mind for evaluating the limits:
(a) Factorisation
(b) Rationalisation or double rationalisation
(c) Use of trigonometric transformation ; appropriate substitution and using standard limits
(d) Expansion of function like Binomial expansion, exponential & logarithmic expansion, expansion of sinx , cosx , tanx should be remembered by heart & are given below :
(i)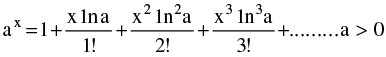
(ii)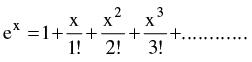
(iii)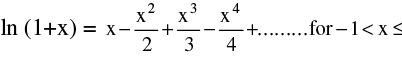
(iv)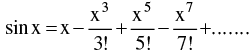
(v) 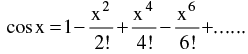
(vi) 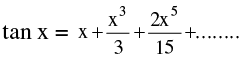
(vii)
(viii)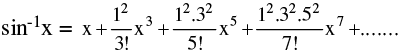
(ix) 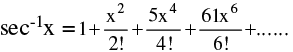
(Continuity)
Things To Remember :
1. A function f(x) is said to be continuous at x = c, if 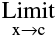 f(x) = f(c). Symbolically f is continuous at x = c if
f(x) = f(c). Symbolically f is continuous at x = c if 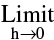 f(c - h) =
f(c - h) =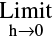 f(c+h) = f(c).
f(c+h) = f(c).
i.e. LHL at x = c = RHL at x = c equals Value of ‘f’ at x = c.
It should be noted that continuity of a function at x = a is meaningful only if the function is defined in the immediate neighbourhood of x = a, not necessarily at x = a.
2. Reasons of discontinuity:
(i) 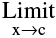 f(x) does not exist
f(x) does not exist
i.e. 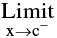 f(x) ≠
f(x) ≠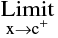 f (x)
f (x)
(ii) f(x) is not defined at x= c
(iii) 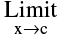 f(x) ≠ f (c)
f(x) ≠ f (c)
Geometrically, the graph of the function will exhibit a break at x= c.
The graph as shown is discontinuous at x = 1 , 2 and 3.
3. Types of Discontinuities :
Type - 1: ( Removable type of discontinuities)
In case 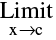 f(x) exists but is not equal to f(c) then the function is said to have a removable discontinuity or discontinuity of the first kind. In this case we can redefine the function such that
f(x) exists but is not equal to f(c) then the function is said to have a removable discontinuity or discontinuity of the first kind. In this case we can redefine the function such that 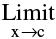 f(x) = f(c) & make it continuous at x= c. Removable type of discontinuity can be further classified as :
f(x) = f(c) & make it continuous at x= c. Removable type of discontinuity can be further classified as :
(a) Missing Point Discontinuity : Where 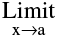 f(x) exists finitely but f(a) is not defined.
f(x) exists finitely but f(a) is not defined.
e.g. f(x) = 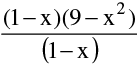 has a missing point discontinuity at x = 1 , and f(x) =
has a missing point discontinuity at x = 1 , and f(x) = 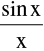
has a missing point discontinuity at x = 0
(b) Isolated Point Discontinuity : Where 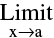 f(x) exists & f(a) also exists but ;
f(x) exists & f(a) also exists but ; 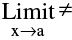 f(a). e.g. f(x)
f(a). e.g. f(x) 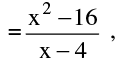 x ≠ 4 & f (4) = 9 has an isolated point discontinuity at x = 4.
x ≠ 4 & f (4) = 9 has an isolated point discontinuity at x = 4.
Similarly f(x) = [x] + [ –x] = 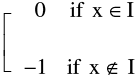 has an isolated point discontinuity at all x ∈ I.
has an isolated point discontinuity at all x ∈ I.
Type-2: (Non - Removable type of discontinuities)
In case  f(x) does not exist then it is not possible to make the function continuous by redefining it.
f(x) does not exist then it is not possible to make the function continuous by redefining it.
Such discontinuities are known as non - removable discontinuity or discontinuity of the 2nd kind. Non-removable type of discontinuity can be further classified as :
(a) Finite discontinuity e.g. f(x) = x − [x] at all integral x ; f(x) = tan −1 at x = 0 and f(x) =
at x = 0 and f(x) = 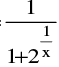 at x = 0 (note that f(0+) = 0 ; f(0–) = 1)
at x = 0 (note that f(0+) = 0 ; f(0–) = 1)
(b) Infinite discontinuity e.g. f(x) = 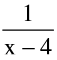 or g(x) =
or g(x) = 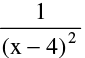 at x = 4 ; f(x) = 2tanx at x =
at x = 4 ; f(x) = 2tanx at x = 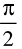 and f(x) =
and f(x) =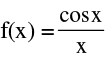 at x = 0.
at x = 0.
(c) Oscillatory discontinuity e.g. f(x) = sin 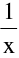 at x = 0.
at x = 0.
In all these cases the value of f(a) of the function at x= a (point of discontinuity) may or may not exist but 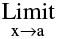 does not exist.
does not exist.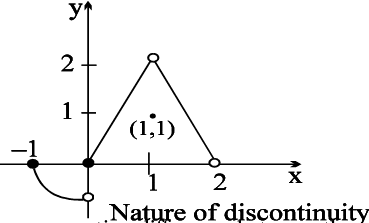
Note: From the adjacent graph note that
– f is continuous at x = – 1
– f has isolated discontinuity at x = 1
– f has missing point discontinuity at x = 2
– f has non removable (finite type)
discontinuity at the origin.
4. In case of dis-continuity of the second kind the non-negative difference between the value of the RHL at x = c & LHL at x = c is called The Jump Of Discontinuity. A function having a finite number of jumps in a given interval I is called a Piece Wise Continuous Or Sectionally Continuous function in this interval.
5. All Polynomials, Trigonometrical functions, exponential & Logarithmic functions are continuous in their domains.
6. If f & g are two functions that are continuous at x= c then the functions defined by :
F1(x) = f(x) ± g(x) ; F2(x) = K f(x) , K any real number ; F3(x) = f(x).g(x) are also continuous at x= c.
Further, if g (c) is not zero, thenF4(x) = 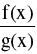 is also continuous atx= c.
is also continuous atx= c.
7. The intermediate value theorem:
Suppose f(x) is continuous on an interval I , and a and b are any two points of I. Then if y0 is a number between f(a) and f(b) , their exists a number c between a and b such that f(c) = y0 .
Note Very Carefully That :
(a) If f(x) is continuous & g(x) is discontinuous
at x = a then the product function φ(x) = f(x). g(x)
is not necessarily be discontinuous at x = a. e.g. f(x) = x & g(x) = 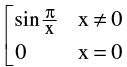
(b) If f(x) and g(x) both are discontinuous at x = a then the product function φ(x) = f(x). g(x) is not necessarily be discontinuous at x = a. e.g. f(x) = − g(x) = 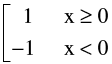
(c) Point functions are to be treated as discontinuous. eg. f(x) = 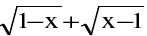 is not continuous at x = 1.
is not continuous at x = 1.
(d) A Continuous function whose domain is closed must have a range also in closed interval.
(e) If f is continuous at x = c & g is continuous at x = f(c) then the composite g[f(x)] is continuous at x = c. eg. 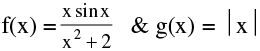 are continuous at x = 0 , hence the composite (gof) (x) =
are continuous at x = 0 , hence the composite (gof) (x) = 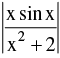 will also be continuous at x = 0 .
will also be continuous at x = 0 .
7. Continuity In An Interval :
(a) A function f is said to be continuous in (a , b) if f is continuous at each & every point ∈(a,b).
(b) A function f is said to be continuous in a closed interval [a , b] if :
(i) f is continuous in the open interval (a , b) &
(ii) f is right continuous at ‘a’ i.e.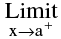 f(x) = f(a) = a finite quantity.
f(x) = f(a) = a finite quantity.
(iii) f is left continuous at ‘b’ i.e.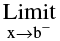 f(x) = f(b) = a finite quantity.
f(x) = f(b) = a finite quantity.
Note that a function f which is continuous in [a , b] possesses the following properties :
(i) If f(a) & f(b) possess opposite signs, then there exists at least one solution of the equation f(x) = 0 in the open interval (a , b).
(ii) If K is any real number between f(a) & f(b), then there exists at least one solution of the equation f(x) = K in the open inetrval (a , b).
8. Single Point Continuity:
Functions which are continuous only at one point are said to exhibit single point continuity
e.g. f(x) = 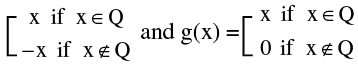 are both continuous only at x = 0.
are both continuous only at x = 0.
Differentiability
Things To Remember :
1. Right hand & Left hand Derivatives ; By definition: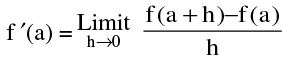 if it exist
if it exist
(i) The right hand derivative of f ′ at x = a denoted by f ′(a+) is defined by :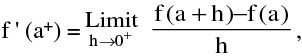
provided the limit exists & is finite.
(ii) The left hand derivative : of f at x = a denoted by
f ′(a+) is defined by : f ' (a–) = 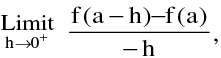 Provided the limit exists & is finite.
Provided the limit exists & is finite.
We also write f ′(a+) = f ′+(a) & f ′(a–) = f ′_(a).
* This geomtrically means that a unique tangent with finite slope can be drawn at x = a as shown in the figure.
(iii) Derivability & Continuity :
(a) If f ′(a) exists then f(x) is derivable at x= a ⇒ f(x) is continuous at x = a.
(b) If a function f is derivable at x then f is continuous at x.
For : f ′(x) = 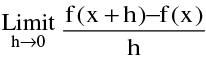 exists.
exists.
Also f(x + h)-f(x)= 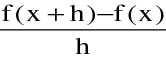 h[h ≠ 0]
h[h ≠ 0]
Therefore : [f (x + h )− f (x)] 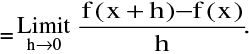 h = f '( x ).0 = 0
h = f '( x ).0 = 0
Therefore 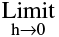 [f ( x + h )− f (x )] = 0 ⇒
[f ( x + h )− f (x )] = 0 ⇒ 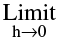 f (x+h) = f(x) ⇒ f is continuous at x.
f (x+h) = f(x) ⇒ f is continuous at x.
Note : If f(x) is derivable for every point of its domain of definition, then it is continuous in that domain.
The Converse of the above result is not true:
“ IF f IS CONTINUOUS AT x , THEN f IS DERIVABLE AT x ” IS NOT TRUE.
e.g. the functions f(x) =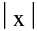 & g(x) = x sin
& g(x) = x sin 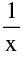 ; x ≠ 0 & g(0) = 0 are continuous at x = 0 but not derivable at x = 0.
; x ≠ 0 & g(0) = 0 are continuous at x = 0 but not derivable at x = 0.
Note Carefully :
(a) Let f ′+(a) = p & f ′_(a) = q where p & q are finite then :
(i) p = q ⇒ f is derivable at x = a ⇒ f is continuous at x = a.
(ii) p ≠ q ⇒ f is not derivable at x = a.
It is very important to note that f may be still continuous at x = a.
In short, for a function f :
Differentiability ⇒ Continuity ; Continuity ⇏ derivability ;
Non derivibality ⇏ discontinuous ; But discontinuity ⇒ Non derivability
(b) If a function f is not differentiable but is continuous at x = a it geometrically implies a sharp corner at x = a.
3. Derivability Over An Interval :
f (x) is said to be derivable over an interval if it is derivable at each & every point of the interval f(x) is said to be derivable over the closed interval [a, b] if :
(i) for the points a and b, f ′(a+) & f ′(b −) exist &
(ii) for any point c such that a < c < b, f ′(c+) & f′(c −) exist & are equal.
Note:
1. If f(x) & g(x) are derivable at x = a then the functions f(x) + g(x), f(x) - g(x) , f(x).g(x) will also be derivable at x = a & if g (a) ≠ 0 then the function f(x)/g(x) will also be derivable at x = a.
2. If f(x) is differentiable at x = a & g(x) is not differentiable at x = a , then the product function F(x) = f(x) g(x) can still be differentiable at x = a e.g. f(x) = x & g(x) = I x |.
3. If f(x) & g(x) both are not differentiable at x = a then the product function ;
F(x) = f(x)- g(x) can still be differentiable at x = a e.g. f(x) = | x | & g(x) = I x |.
4. If f(x) & g(x) both are non-deri. at x = a then the sum function F(x) = f(x) + g(x) may be a differentiable function. e.g. f(x) = | x | & g(x) = -| x |.
5. If f(x) is derivable at x = a ⇏ f '(x) is continuous at x = a.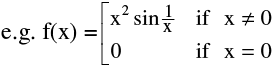
6. A surprising result : Suppose that the function f (x) and g (x) defined in the interval (x1, x2) containing the point x0, and if f is differentiable at x = x0 with f (x0) = 0 together with g is continuous as x = x0 then the function F (x) = f (x) · g (x) is differentiable at x = x0 e.g. F (x) = sinx · x2/3 is differentiable at x = 0.
|
172 videos|476 docs|154 tests
|
















