Important Important Formulas - 3D Geometry Formulas for JEE and NEET
3 -D Coordinate Geometry
(1) Distance (d) between two points (x1 , y1 , z1) and (x2 , y2 , z2).
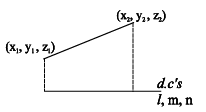 =
=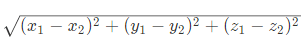
(2) Direction Cosine and direction ratio's of a line 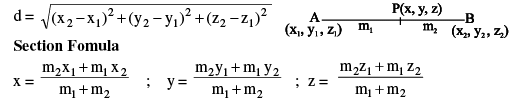
(3) Direction cosine of a line has the same meaning as d.c's of a vector.
(a) Any three numbers a, b, c proportional to the direction cosines are called the direction ratio s i.e.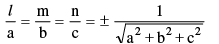
same sign either +ve or –ve should be taken throughout.
note that d.r's of a line joining x1 , y1 , z1 and x2 , y2 , z2 are proportional to x2 – x1 , y2 – y1 and z2 – z1
(b) If θ is the angle between the two lines whose d.c's are l1 , m1 , n1 and l2 , m2 , n2 cosθ = l1 l2 + m1 m2+n1 n2 hence if lines are perpendicular then l1 l2 + m1m2+ n1 n2 = 0
if lines are parallel then
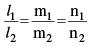
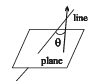
note that if three lines are coplanar then 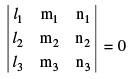
(4)Projection of join of 2 points on line with d.c's l, m, n are l (x2 – x1) + m(y2 – y1) + n(z2 – z1) B PLANE
(i) General equation of degree one in x, y, z i.e. ax + by + cz + d = 0 represents a plane. (ii) Equation of a plane passing through (x1 , y1 , z1) is a (x – x1) + b (y – y1) + c (z – z1) = 0 where a, b, c are the direction ratios of the normal to the plane.
(iii) Equation of a plane if its intercepts on the co-ordinate axes are x1 , y1 , z1 is z 1 z
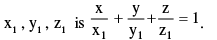
(iv) Equation of a plane if the length of the perpendicular from the origin on the plane is p and d.c's of the perpendicular as l , m, , n is l x + m y + n z = p
(v) Parallel and perpendicular planes – Two planes a1 x + b1 y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0 are perpendicular if a1 a2 + b1 b2 + c1 c2 = 0,
parallel if 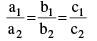 and coincident if
and coincident if 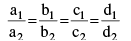
(vi) Angle between a plane and a line is the compliment of the angle between the normal to the plane and the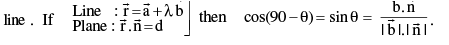
where θ is the angle between the line and normal to the plane.
(vii) Length of the perpendicular from a point (x1 , y1 , z1) to a plane ax + by + cz + d = 0 is 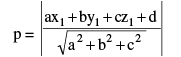
(viii) Distance between two parallel planes ax + by + cz + d1 = 0 and ax+by + cz + d2 = 0 is 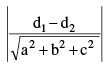
(ix) Planes bisecting the angle between two planes a1x + b1y + c1z + d1 = 0 and a2 + b2y + c2z + d2 = 0 is
Given by 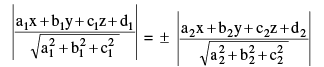
Of these two bisecting planes , one bisects the acute and the other obtuse angle between the given planes.
(x) Equation of a plane through the intersection of two planes P1 and P2 is given by P1+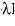 P2=0
P2=0
C Straight Line in Space
(i) Equation of a line through A (x1 , y1 , z1) and having direction cosines l ,m , n are
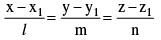 and the lines through (x1 , y1 ,z1) and (x2 , y2 ,z2).
and the lines through (x1 , y1 ,z1) and (x2 , y2 ,z2).
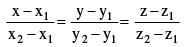
(ii) Intersection of two planes a1x + b1y + c1z + d1 = 0 and a2x + b2y + c2z + d2 = 0 together represent the unsymmetrical form of the straight line.
(iii) General equation of the plane containing the line 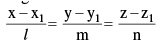
is A (x – x1) + B(y – y1) + c (z – z1) = 0 where Al + bm + cn = 0 .
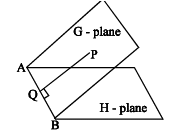
Line of greatest slope
AB is the line of intersection of G-plane and H is the horizontal plane. Line of greatest slope on a given plane, drawn through a given point on the plane, is the line through the point 'P' perpendicular to the line of intersetion of the given plane with any horizontal plane.
|
209 videos|447 docs|187 tests
|
FAQs on Important Important Formulas - 3D Geometry Formulas for JEE and NEET
| 1. What are the formulas for finding the distance between two points in 3D geometry? |  |
| 2. How do I calculate the midpoint between two points in 3D space? |  |
| 3. What is the formula for finding the equation of a plane in 3D geometry? |  |
| 4. How can I find the angle between two vectors in 3D space? |  |
| 5. How do I calculate the volume of a parallelepiped in 3D geometry? |  |




















