Important Formulas for CAT Coordinate Geometry
- Distance between two points P(x1,y1) and Q(x2,y2) is given by =
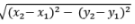
- If a point R (x,y) divides P(x1,y1) and Q(x2,y2) internally in the ratio of m:n, the coordinates of R ie (x,y) are given by
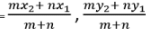
- If a point R (x,y) divides P(x1,y1) and Q(x2,y2) externally in the ratio of m:n, the coordinates of R ie (x,y) are given by
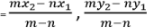
EduRev's Tip:
- The X axis divides the line joining P(x1,y1) and Q(x2,y2) in the ratio of y1 : y2
- The Y axis divides the line joining P(x1,y1) and Q(x2,y2) in the ratio of x1 : x2
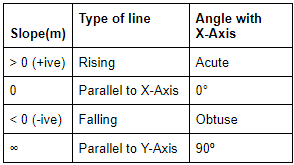
Slope(m) of a line is the tangent of the angle made by the line with the positive direction of the X-Axis.
For a general equation ax + by + c = 0; slope (m) = -a/b.
For a line joining two points, P (x1,y1) and Q(x2,y2), the slope(m) is = 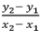
Equation of a line parallel to X-axis is y = a {Of X-Axis is y = 0}
Equation of a line parallel to Y-Axis is x = a {Of Y-Axis is x = 0}
The intercept of a line is the distance between the point where it cuts the X-Axis or Y-Axis and the origin. Y-Intercept is often denoted with the letter ‘c’.
Equation of a line
General form: ax + by + c = 0
Slope Intercept Form: Slope is m, y-intercept is c
⇒ y = mx + c
Slope Point Form: Slope is m, point is x1,y1
⇒ y – y1 = m(x – x1)
Two Point Form: Two points are x1,y1 and x2,y2
⇒ 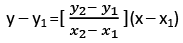
Two Intercept Form: X-intercept is a, Y-intercept is b.
⇒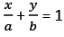 OR bx + ay = ab
OR bx + ay = ab
A cute angle between two lines with slope m1 and m2 is given by
⇒ 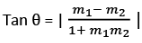
⇒ For parallel lines, θ = 0°; m1 = m2
⇒ For parallel lines, θ = 90°; m1m2 = -1
Distance of a point P (x1,y1) from a line ax + by + c = 0
⇒ 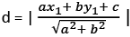
⇒ From origin, d = 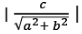
Distance between two parallel lines, ax + by + c1 = 0 and ax + by + c2 = 0
⇒ 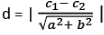
EduRev's Tip: If we know three points A(x1,y1), B(x2,y2 ) and C(x2,y2) of a parallelogram, the fourth point is given by
⇒ (x1 + x3 – x2, y1 + y3 – y2)
Triangle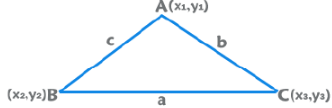
The vertices are P (x1,y1), Q(x2,y2) and R(x3,y3)
Incenter 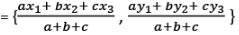
Centroid = 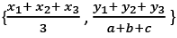
Area = ½ [ x1(y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2)]
Circle
General Equation: x2 + y2 + 2gx + 2fy + c = 0
⇒ Centre is (-g, -f) and radius = 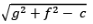
Centre is (h, k) and radius is r
⇒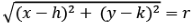
Centre is origin and radius is r
⇒ x2 + y2 = r2
|
166 videos|231 docs|95 tests
|
FAQs on Important Formulas for CAT Coordinate Geometry
| 1. What are the formulas for finding the distance between two points in coordinate geometry? |  |
| 2. How do I find the midpoint of a line segment in coordinate geometry? |  |
| 3. What is the formula for finding the slope of a line in coordinate geometry? |  |
| 4. How can I determine if three points in coordinate geometry are collinear? |  |
| 5. What is the formula for finding the equation of a straight line in coordinate geometry? |  |





















